Post by: Æthelwulf on 15/04/2012 20:21:30
Of course, how do you speak about space or even time if niether existed fundamentally? Fotini Markoupoulou has been using a special model. In her recent idea's, she believes that space is not fundamental.
In her model, simply put, particles are represented by points which are nodes which can be on or off, which represents whether the nodes are actually interacting. Only at very high temperatures, spacetime ceases to exist and many of us will appreciate this as Geometrogenesis. The model also obeys the Causal Dynamical Triangulation which is a serious major part of quantum loop gravity theory which must obey the triangle inequality in some spin-state space. Spin state spaces may lead to models we can develop from the Ising Model or perhaps even Lyapanov Exponential which measures the seperation of objects in some Hilbert spaces preferrably. We may in fact be able to do a great many things.
Heisenberg uncertainty is a form of the geometric Cauchy Schwarz inequality law and this might be a clue to how to treat spacetime so unstably at very early beginnings when temperatures where very high.
http://www.scribd.com/doc/15501464/CauchySchwarz-Inequality-and-Heisenbergs-Uncertainty-Principle
Since Markoupoulou's work is suggesting that particles exist on Hilbert Spaces in some kind of special sub-structure before the emergence of geometry, then now I can approach my own theory and answer it in terms of the uncertainty principle using the Cauchy-Shwartz inequality because from this inequality one can get the triangle inequality.
So, this is my idea. Space and time emerged between particles because particles could not be allowed to infinitely remain confined so close to other particles, that the uncertainty forbid it and created degrees of freedom in the form of the vacuum we see expanding all around us.
I'll write up some math later.
Post by: Æthelwulf on 15/04/2012 20:43:20
Post by: imatfaal on 16/04/2012 10:08:58
Post by: Æthelwulf on 16/04/2012 10:18:14
no - not nuts, but def a new theory.
Good, then, I will begin to write out the math I have been fiddling about with later.
Post by: Æthelwulf on 17/04/2012 05:36:24
So let me explain how this model works. First of all, it seems best to note that in most cases we are dealing with ''three neighbouring points'' on what I call a Fotini graph. Really, the graph has a different name and is usually denoted with something like
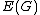and is sometimes called the graphical tensor notation. In our phase space, we will be dealing with a finite amount of particles 
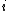and 
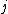but asked to keep in mind that the neighbouring particles are usually seen at a minimum three and that each particle should be seen as a configuration of spins - this configuration space is called the spin network. I should perhaps say, that to any point, there are two neighbours.Of course, as I said, we have two particles in this model
, probably defined by a set of interactions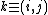 
(an approach Fotini has made in the form of on-off nodes). In my approach we simply define it with an interaction term: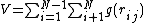
I have found it customary to place a coupling constant here
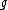for any constant forces which may be experienced between the two distances made in a semi-metric which mathematicians often denote as 
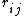.If
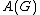are adjacent vertices and 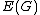is the set of edges in our phase space, (to get some idea of this space, look up casual triangulation and how particles would be laid out in such a configuration space), then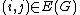 
It so happens, that Fotini's approach will in fact treat
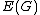as assigning energy to a graph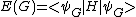 
which most will recognize as an expection value. The Fotini total state spin space is
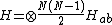
Going back to my interaction term, the potential energy between particles
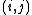or all 
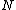-particles due to pairwise interctions involves a minimum of 
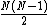contributions and you will see this term in Fotini's previous yet remarkably simple equation.
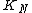is the complete graph on the 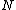- vertices in a Fotini Graph i.e. the graph in which there is one edge connecting every pair of vertices so there is a total of 
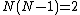edges and each vertex has a degree of freedom corresponding to 
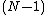.Thus we will see that to each vertex
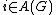there is always an associated Hilbert space and I construct that understanding as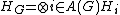
From here I construct a way to measure these spin states in the spin network such that we are still speaking about two particles
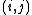and by measuring the force of interaction between these two states as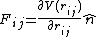
where the
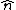is the unit length. The angle between two spins in physics can be calculated as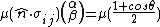
Thus my force equation can take into respect a single spin state, but denoted for two particles
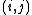as we have been doing, it can describe a small spin network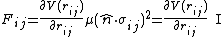
with a magnetic coefficient
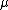on the spin structure of the equation and 
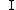is the unit matrix.I now therefore a new form of the force equation I created with an interaction term, as I came to the realization that squaring everything would yield (with our spin states)
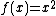
Sometimes it is customary to represent the matrix in this form:
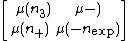
As we have in our equation above. The entries here are just short hand notation for some mathematical tricks. Notice that there is a magnetic moment coupling on each state entry. We will soon see how you can derive the Larmor Energy from the previous equation.
Sometimes you will find spin matrices not with the magnetic moment description but with a gyromagnetic ratio, so we might have
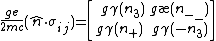
The compact form of the Larmor energy is
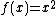and the negative term will cancel due to the negative term in my equation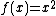
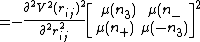
The
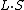part of the Larmor energy is in fact more or less equivalent with the spin notation expression I have been using 
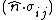, except when we transpose this over to our own modified approach, we will be accounting for two spins.We can swap our magnetic moment part for
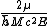and what we end up with is a slightly modified Larmor Energy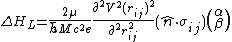
This is madness I can hear people shout? In the Larmor energy equation, we don't have
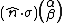we usually have 
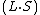?Well yes, this is true, but we are noticing something special. You see,
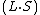is really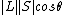
This is the angle between two vectors. What is
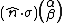again? We know this, it calculates the angle between two spin vectors again as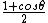
So by my reckoning, this seems perfectly a consistent approach.
Now that we have derived this relationship, it adds some texture to the original equations. If we return to the force equation, one might want to plug in some position operators in there - so we may describe how far particles are from each other by calculating the force of interaction - but as we shall see soon, if the lengths of the triangulation between particles are all zero, then this must imply the same space state, or position state for all your
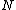-particle system. We will use a special type of uncertainty principle to denote this, called the triangle inequality which speaks about the space between particles. As distances reduce between particles, our interaction term becomes stronger as well, the force between particles is at cost of extra energy being required. Indeed, for two particles
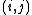to experience the same position 
requires a massive amount of energy, perhaps something on the scale of the Planck Energy, but I have not calculated this.In general, most fundamental interactions do not come from great distance and focus to the same point, or along the same trajectories. This actually has a special name, called Liouville's Theorem. Of course, particles can be created from a point, this is a different scenario. Indeed, in this work I am attempting to built a picture which requires just that, the gradual seperation of particles from a single point by a vacua appearing between them, forced by a general instability caused by the uncertainty principle in our phase space.
As I have mentioned before, we may measure the gradual seperation of particles using the Lyapunov Exponential which is given as
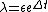
and for previously attached systems eminating from the same system, we may even speculate importance for the correlation function
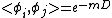
where
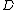calculates the distance. Indeed, you may even see the graphical energy in terms maybe of the Ising model which measures the background energy to the spin state 
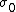- actually said more correctly, the background energy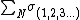
acts as coefficient of sigma zero. Thus the energy is represented by a Hamiltonian of spin states
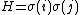
Now, moving onto the implications of the uncertainty principle in our triple intersected phase space (with adjacent edges sometimes given as
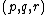, there is a restriction that 
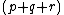is even and none is larger than the sum of the other two. A simpler way of trying to explain this inequality is by stating: 
must be less than or equal to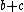 
, 
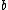less than or equal to 
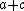, and 
less than or equal to 
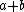.It actually turns out that this is really a basic tensor algebra relationship of the irreducible representions of
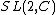according to Smolin. If each length of each point is necesserily zero, then we must admit some uncertainty (an infinite degree of uncertainty) unless some spacetime appeared appeared between each point. Indeed, because each particle at the very first instant of creation was occupied in the same space, we may presume the initial conditions of BB were highly unstable. This is true within the high temperature range and can be justified by applying a strong force of interactions in my force equation. The triangle inequality is at the heart of spin networks and current quantum gravity theory.For spins that do not commute ie, they display antisymmetric properties, there could be a number of ways of describing this with some traditional mathematics. One way will be shown soon.
Spin has close relationships with antisymmetric mathematical properties. An interesting way to describe the antisymmetric properties between two spins in the form of pauli matrices attached to particles
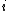and 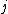we can describe it as an action on a pair of vectors, taking into assumption the vectors in question are spin vectors. This is actually a map, taking the form of
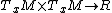
This is amap of an action on a pair of vectors. In our case, we will arbitrarily chose these two to be Eigenvectors, derived from studying spin along a certain axis. In this case, our eigenvectors will be along the
and 
axes which will always yield the corresponding spin operator.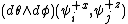
with an abuse of notation in my eigenvectors.
It is a 2-form (or bivector) which results in
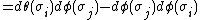
This is a result where
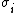and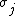 
do not commute.
Post by: Æthelwulf on 17/04/2012 05:43:00
Post by: Æthelwulf on 17/04/2012 05:59:59
Post by: Æthelwulf on 17/04/2012 07:03:21
-\mu \cdot B
with tex symbols
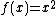
Post by: Æthelwulf on 17/04/2012 19:39:07
http://www.ilovephysics.com/forum/t3909-What-Made-Spacetime-Expand-Singularity%3F.html
Post by: Dharmansh on 18/04/2012 09:04:22
Post by: Æthelwulf on 18/04/2012 09:37:42
Some Black holes are form with the help of two Dwarf planet right?But what happens to dwarf are they fused into one Because of the gravity?Maybe, but I will give you a reserved answer. There are four types of dwarfs I know about, Brown Dwarfs, Red Dwarfs, White Dwarfs and Black Dwarfs. There is a denser object in the universe called a Neutron Star. It is believed that two Neutron Stars may spiral towards each other at near light speed and then crash together sending gravitationl ripples into space: the most likely by-product of the merge would be a black hole.
The reason why this is a reserved answer, is because Neutron Stars are a [lot more] denser than a Dwarf Planet. In short, it may be possible (but this is a guess) that they may not be dense enough to form black holes. Though, I believe I could be wrong and if two of these Dwarfs did spiral towards each other at fast speeds, they might.
Post by: Dharmansh on 24/04/2012 18:20:49
Post by: Æthelwulf on 24/04/2012 18:25:41
If two dwarf fuse in one so how can there be gamma burst?If there is Gamma burst it can be break in two parts?
Gamma particles are released by many nuclear processes. There are many processes I could speak about. Even your odd antiparticle will annihilate with gamma energy.
Post by: Dharmansh on 25/04/2012 14:10:40
Post by: Dharmansh on 25/04/2012 19:08:00
if two of these Dwarfs did spiral towards each other at fast speeds, they might.
[/quote]
Y cant mercury be attracted to sun because of sun's gravity???
Post by: Æthelwulf on 26/04/2012 20:31:06
Y cant mercury be attracted to sun because of sun's gravity???
if two of these Dwarfs did spiral towards each other at fast speeds, they might.
[/quote]
All planets in our solar system is attracted by the suns gravitational force. In fact, all objects atleast theoretically speaking are influenced by every gravitational body in the universe.
Post by: Æthelwulf on 26/04/2012 20:33:06
Thanks...But when two dwarf is fusing in one first they Break into small particles right?So how can they get one?Why are they not attracted with another particles in universe or galaxy?
I don't know about the nucleic processes involved -- I'd need to look it up... But the gravitational forces will be very strong, it would be the main force which ''binds'' the mass together. On a smaller level, we can attribute the ''binding'' to the strong force. Then the electromagnetic forces. Gravity is only significant because we are talking about a body with a substantial density.
Post by: Dharmansh on 29/04/2012 09:58:56
Y cant mercury be attracted to sun because of sun's gravity???
if two of these Dwarfs did spiral towards each other at fast speeds, they might.
All planets in our solar system is attracted by the suns gravitational force. In fact, all objects atleast theoretically speaking are influenced by every gravitational body in the universe.
[/quote]
i m telling dat y can't some planets go inside the sun..see Pluto is revolving around the sun due to sun's gravity pluto is very far... so y is mercury revolving??? y it is not sucked by the sun?
Post by: yor_on on 01/05/2012 17:26:06
Can you expand on how she mean there Wulf, and give us some good links..
Post by: imatfaal on 02/05/2012 09:38:46
Post by: Dharmansh on 03/05/2012 16:10:56
can u tell me?
Post by: Æthelwulf on 06/05/2012 10:38:43
"Since Markoupoulou's work is suggesting that particles exist on Hilbert Spaces in some kind of special sub-structure before the emergence of geometry"
Can you expand on how she mean there Wulf, and give us some good links..
Yes... I will find a good paper... her original one would be the best example. I'll get it in a minute.
Post by: Æthelwulf on 06/05/2012 10:42:35
http://arxiv.org/pdf/0911.5075v3.pdf
My Induced Time theory is like a sister theory to her model, based on separate principles for its arguements.
Post by: Æthelwulf on 06/05/2012 10:44:50
i m telling dat y can't some planets go inside the sun..see Pluto is revolving around the sun due to sun's gravity pluto is very far... so y is mercury revolving??? y it is not sucked by the sun?Y cant mercury be attracted to sun because of sun's gravity???
if two of these Dwarfs did spiral towards each other at fast speeds, they might.
All planets in our solar system is attracted by the suns gravitational force. In fact, all objects atleast theoretically speaking are influenced by every gravitational body in the universe.
[/quote]
They don't fall into the sun directly because they are bound to follow geodesics around the sun - these are curvilinear paths.
Post by: wucko on 13/05/2012 01:04:00
-> there was very much less time much further back, meaning that on 'big scale' the galaxies appeared closer and after much more time in the future, they appear further from each other. There was no beginning (of time). Spacetime had expanded because time is expanding. Leaves problems at 'particle scale'. But what if matter traverses a discrete space (an possible cause of uncertainty principle)? - > this makes it possible for paricles to be extremely close (in space) but never actualy stacked up and so - from any refference t-point - in an infinity of time to past and future. + in curvature - no time, hence:
class discretespace($time) extends uncertaintyprinciple()
{
if (HasCurvature())
{
DoesntExpandWithTime()
}
else
{
ExpandsWithTime() {class DistanceBetweenGalaxies($time) extends DistanceBetweenAnyPairOfObjectsWithMassBeyondTheGravityEffect($time) }
}
}
this is where my intuition leads me regarding expansion, especialy including the odity of faster than light speed of expansion (C constant, time building up (exponentialy?) )
(please allow some time for me to be able to read your math, in the meantime, whats a good text-book for that? :)
Could time as a quantity expand exponentialy between any pair of refference points in time?
Language:
$x -> variable x
foo($bar) -> function foo, with function-argument $bar
class x() -> object property