Post by: guest39538 on 09/07/2017 02:48:32
One recording the ground at point (A) and one much further away at point (B) recording the area of (A)
We then just need lightning to hit the ground, Recorder (A) for example records the strike hitting the ground at 1 min 20.s
Recorder (B) records the strike a short amount of time later.
Compare differences work out the speed of light over distance x
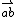
cam.jpg (22.19 kB . 985x507 - viewed 6477 times)Time line (A) shows 1 minutes 20.s the lightning strikes the ground
Time line (B) shows 1 minutes 20.1s the lightning strikes the ground
So in this example the light travelled a 1000m in 0.1s because camera (B) was 1000m away exact.
ok?
Post by: Bored chemist on 09/07/2017 09:44:10
That's where the problems start.
But, if we can assume that local gravity is small enough that it has little effect and that the cameras are synchronised while next to each other then moved apart sufficiently slowly that relativistic effects are small and that you bring the cmaeras together again slowly to compare the recordings. then yes.
You can use that setup to measure the speed of light.
However, one way of "synchronising" the videos would be to wait for a lightning strike and say that, since it clearly was only 1 event it must happen at the same time for both cameras.
Then you get into problems.
Post by: guest39538 on 09/07/2017 15:18:35
"2 video cameras that are synchronised in their start. 0t"The synchronisation is a lot easier than you think, the cameras can already be recording in situate position before we synchronise them, the only synchronisation needed on the videos is the timelines, 1 reset button tarring both recorders to 0 to synchronise recordings.
That's where the problems start.
But, if we can assume that local gravity is small enough that it has little effect and that the cameras are synchronised while next to each other then moved apart sufficiently slowly that relativistic effects are small and that you bring the cmaeras together again slowly to compare the recordings. then yes.
You can use that setup to measure the speed of light.
However, one way of "synchronising" the videos would be to wait for a lightning strike and say that, since it clearly was only 1 event it must happen at the same time for both cameras.
Then you get into problems.
Post by: Bored chemist on 09/07/2017 15:52:32
The synchronisation is a lot easier than you think, the cameras can already be recording in situate position before we synchronise them, the only synchronisation needed on the videos is the timelines, 1 reset button tarring both recorders to 0 to synchronise recordings.No they can't.
Simultaneity is only defined locally. You have to take account of how long it takes for the signal saying you pressed the "zero button" to get to the two videos.
Since you seem to be trying to set up a thread about relativity, I think you might start by learning about it
Post by: guest39538 on 09/07/2017 17:18:25
This is a thread about measuring the speed of light if not testing simultaneity.The synchronisation is a lot easier than you think, the cameras can already be recording in situate position before we synchronise them, the only synchronisation needed on the videos is the timelines, 1 reset button tarring both recorders to 0 to synchronise recordings.No they can't.
Simultaneity is only defined locally. You have to take account of how long it takes for the signal saying you pressed the "zero button" to get to the two videos.
Since you seem to be trying to set up a thread about relativity, I think you might start by learning about it
Post by: Bored chemist on 09/07/2017 19:25:06
They are strongly related.This is a thread about measuring the speed of light if not testing simultaneity.The synchronisation is a lot easier than you think, the cameras can already be recording in situate position before we synchronise them, the only synchronisation needed on the videos is the timelines, 1 reset button tarring both recorders to 0 to synchronise recordings.No they can't.
Simultaneity is only defined locally. You have to take account of how long it takes for the signal saying you pressed the "zero button" to get to the two videos.
Since you seem to be trying to set up a thread about relativity, I think you might start by learning about it
Post by: guest39538 on 09/07/2017 20:08:40
Well I suppose so. My mate just shown me something, the great pyramids earthly co-ordinates the same as the speed of light in numbers?They are strongly related.This is a thread about measuring the speed of light if not testing simultaneity.The synchronisation is a lot easier than you think, the cameras can already be recording in situate position before we synchronise them, the only synchronisation needed on the videos is the timelines, 1 reset button tarring both recorders to 0 to synchronise recordings.No they can't.
Simultaneity is only defined locally. You have to take account of how long it takes for the signal saying you pressed the "zero button" to get to the two videos.
Since you seem to be trying to set up a thread about relativity, I think you might start by learning about it
Post by: dutch on 14/07/2017 18:38:11
It's NOT showing that you can measure the one-way speed of light independent of two spatially separated clocks.This has never been done.
https://en.wikipedia.org/wiki/One-way_speed_of_light
https://en.wikipedia.org/wiki/Einstein_synchronisation
Quote
Einstein synchronization (or Poincaré–Einstein synchronization) is a convention for synchronizing clocks
Quote
Most attempts to negate the conventionality of this synchronization are considered refuted
But, if we can assume that local gravity is small enough that it has little effect and that the cameras are synchronized while next to each other then moved apart sufficiently slowly that relativistic effects are small and that you bring the cameras together again slowly to compare the recordings. then yes.
But from who's perspective is the relativistic effect small?
To an observer's moving at 90% the speed of light past one clock then the other relative to the spatially separated clocks the simultaneity difference is rather extreme. Slow clock transport in one direction would be vastly different than slow clock transport in the other direction according to this observer. The clocks are out of sync according to this observer. However, this moving frame of reference is equally valid and stands on equal footing as another inertial reference frame. Einstein showed that slow clock transport and fast clock synchronization (sync clocks with light) were identical. Einstein and most physicists (who actually study up on this subject) know that "Einstein Clock Synchronization" is a convention. A very useful convention but a convention nevertheless.
Post by: guest39538 on 15/07/2017 00:58:23
What is this experiment trying to show?
It's NOT showing that you can measure the one-way speed of light independent of two spatially separated clocks.
Yeah , I have a vague idea how to do it.
Post by: guest39538 on 15/07/2017 02:18:44
cc.jpg (21.85 kB . 1152x648 - viewed 6147 times)Maybe 3 cameras for triangulation.
Post by: puppypower on 15/07/2017 11:39:44
Post by: Bored chemist on 15/07/2017 12:12:46
For the sake of discussion, mine.
But from who's perspective is the relativistic effect small?
I'm sat round near one of the cameras. and both cameras are on the ground. All of us are stationary wrt one another.
I took a while, and I delivered the cameras to their locations three million meters apart by bicycle. They certainly never exceeded 30 m/s i.e. C/10,000,000 .
Most of the time they were travelling at about a millionth of C
And I found a "flat" bit of the Earth to use as my baseline. There were no hills on my journey.
So the relativistic effects on the clocks due to their changes in velocity and altitude (thus gravity) were small.
If you are not content that they are small enough we can, in principle, repeat the experiment with cameras delivered by snails or even continental drift.
"To an observer's moving at 90% the speed of light past one clock"
OK, so we won't ask him, we will ask me.
I set off a flash bulb near one of the cameras. and the cameras capture that flash.
Then I go and collect the cameras and I develop the films.
They are slightly odd cameras (since this is just a thought experiment). They use old fashioned film and they run at a million frames per second.
I count the frames in each film until I reach the frame with the flash in it (never-mind how long a real flash takes- this is a thought experiment).
There are lots of frames but the important thing is the difference in frame number.
I find that the camera near the flash records it on frame number n and the one far away records it on frame number n+m.
So it takes m millionths of a second for the flash to travel 3 million metres from the first camera to the second camera.
Now, I know from other experiments - Fizeau and so on, that the speed of light is about 300 million metres per second.
So I expect it to take about a hundredth of a second to make the journey.
Each frame takes a microsecond, so I should find that m is about 10,000
What value of m do you expect to find?
Post by: dutch on 16/07/2017 04:18:40
For the sake of discussion, mine.
I'm sat round near one of the cameras. and both cameras are on the ground. All of us are stationary wrt one another.
I took a while, and I delivered the cameras to their locations three million meters apart by bicycle. They certainly never exceeded 30 m/s i.e. C/10,000,000 .
Most of the time they were travelling at about a millionth of C
And I found a "flat" bit of the Earth to use as my baseline. There were no hills on my journey.
So the relativistic effects on the clocks due to their changes in velocity and altitude (thus gravity) were small.
If you are not content that they are small enough we can, in principle, repeat the experiment with cameras delivered by snails or even continental drift.
"To an observer's moving at 90% the speed of light past one clock"
OK, so we won't ask him, we will ask me.
I set off a flash bulb near one of the cameras. and the cameras capture that flash.
Then I go and collect the cameras and I develop the films.
They are slightly odd cameras (since this is just a thought experiment). They use old fashioned film and they run at a million frames per second.
I count the frames in each film until I reach the frame with the flash in it (never-mind how long a real flash takes- this is a thought experiment).
There are lots of frames but the important thing is the difference in frame number.
I find that the camera near the flash records it on frame number n and the one far away records it on frame number n+m.
So it takes m millionths of a second for the flash to travel 3 million metres from the first camera to the second camera.
Now, I know from other experiments - Fizeau and so on, that the speed of light is about 300 million metres per second.
So I expect it to take about a hundredth of a second to make the journey.
Each frame takes a microsecond, so I should find that m is about 10,000
What value of m do you expect to find?
None of this is measuring the one-way speed of light independent of two spatially separated clocks. Measuring the one-way speed of light by ANY experiment ever done or probably could be done doesn't measure the one-way speed of light without using a synchronization convention. There has never been any way around this. You're assuming clocks are running at the same rate, the clocks are synchronized, and the one-way speed of light is the same in both directions. You can always assume these to be true from your point of view... because you can choose any valid point of view. However, you can ask any inertial reference frame their point of view because they are all equally valid. From other reference frame's points of view your assumptions aren't true. These other inertial reference frames can produce the exact same physics and you could also use their synchronization to produce the exact same predictions. They could easily predict what you'd see in your reference frame when using their synchronization. They can predict vastly different relative speeds for light in different directions relative to your reference frame because they are assuming their reference frame's synchronization (how great depends on their velocity relative to you).
Quote
OK, so we won't ask him, we will ask me.
You could run all your math off of the other inertial reference frame. You could even join a religion where you believe the other inertial reference frame is the "right" one and thus use it and only it. You assume the Einstein Synchronization (some people assume it like its a religion) because you can but not because it was ever proven as the only synchronization (in fact there are infinitely many). Why did you assume you're particular synchronization? I don't think you understand how many assumptions you're making. Did you read the following below? It's a very strong statement.
Quote
Most attempts to negate the conventionality of this synchronization are considered refuted
You could say the two-way speed of light has been measured. You could even say information moves slower or at the vacuum speed of light in all experiments ever done. As proven by Einstein you could say slow clock transport and fast clock transport are identical (you assume the opposite for some reason. Your assumption is wrong; Transport an actual clock slowly from point a to b using the Lorentz Transformation. Use a light clock for simplicity to visualize your error)
However, the one-way speed of light is only measured based on an assumed synchronization. Regardless of how one chooses to view relativity the one-way speed of light is a lot more subtle than most think.
I have thought some more, if we had the two cameras recording the one location live and two corresponding monitors of each camera, we should be able to observe a flash of lightning on one screen before the second screen . .....Then if some how we can measure the time difference in screens, we should be able to calculate a speed.
If you could do it then you may have something but that's a rather big if. People have been saying they've measured the one-way speed of light independent of a clock synchronization convention for over 100 years but they never have. Amusingly, they attempt to measure this value to defend Einstein's Relativity unnecessarily because it was Einstein who showed that you couldn't.
Post by: Bored chemist on 16/07/2017 10:11:00
You don't seem to have included an answer to my question.
What value do you expect me to get for m?
After that we can consider the more complicated cases like spacemen who believe in unicorns if that's what we want to, but simply not answering a question isn't helpful
Incidentally, it's not so much that I assume that slow transport doesn't dilate time.
It's that I know that people who know more about t than I do assumed that fast transport dilated time more.
Are you saying that teh people who did this experiment
https://en.wikipedia.org/wiki/Hafele%E2%80%93Keating_experiment
should have used a rowing boat, rather than a jet plane?
Incidentally, I'd like to introduce a slight refinement to the thought experiment.
Imagine that , in the field of view of each camera is a clock counting (local) microseconds.
That will number the frames for me and stop me needing to count them.
With that amendment we can talk about what time things are recorded as happening from the point of view of each camera.
Post by: dutch on 16/07/2017 20:54:39
In doing science by thought experiments it's not exactly rare to start with the simplest possible case as a foundation.That's pretty much the case I have considered.
You don't seem to have included an answer to my question.
What value do you expect me to get for m?
The answer to your question is straight out of the Lorentz Transformation and I did answer it. See below:
They could easily predict what you'd see in your reference frame when using their synchronization.
In fact you could use their synchronization to synchronize your clocks (simply use the Lorentz Transformation). In practice it's often easier to assume Einstein Synchronization but it's still a convention.
After that we can consider the more complicated cases like spacemen who believe in unicorns if that's what we want to, but simply not answering a question isn't helpful
Relativity allows us to use any valid reference frame we wish. This has nothing to do with unicorns or spacemen. It has to do with hard physics. I've done quite complicated particle physics problems based solely off of the lab reference frame. I've also done them off of other particular reference frames as it suited the problem (often vastly different than the lab frame). Regardless of what reference fame I choose the observations are the same. The relative speed of light outside of my choice of reference frame (and thus my chosen synchronization) could be vastly different than c and different in different directions. I don't have to choose isotropy for my own reference frame to get the right answer. However, I always have the choice to choose isotropy.
Incidentally, it's not so much that I assume that slow transport doesn't dilate time.
It's that I know that people who know more about t than I do assumed that fast transport dilated time more.
Are you saying that teh people who did this experiment
https://en.wikipedia.org/wiki/Hafele%E2%80%93Keating_experiment
should have used a rowing boat, rather than a jet plane?
No, but in terms of spatially separated clock synchronization it doesn't matter if you transport the clocks slow or fast. Do you want me to do the math? I don't care about the round trip time dilation as this is a related but separate effect (Twins Paradox). The issue at hand is the synchronization of the clocks for t = 0 ( the γ v x / c² term and not the time dependent γ t term). It's the change in simultaneity from point a to b not how fast clocks run relative to another reference frame as time ticks forward.
The Lorentz Time Transformation is below:
t' = γ ( t - v x / c²)
Incidentally, I'd like to introduce a slight refinement to the thought experiment.
Imagine that , in the field of view of each camera is a clock counting (local) microseconds.
That will number the frames for me and stop me needing to count them.
With that amendment we can talk about what time things are recorded as happening from the point of view of each camera.
You still can't measure the one-way speed of light independent of a clock synchronization. This is a subtle but very important point coming out of Relativity.
Post by: Bored chemist on 16/07/2017 22:07:52
There has never been any way around this. You're assuming clocks are running at the same rate, the clocks are synchronized, and the one-way speed of light is the same in both directions.Yes, I know I'm making those assumptions (and some others).
Under what circumstances are they invalid?
Post by: dutch on 16/07/2017 23:03:36
Yes, I know I'm making those assumptions (and some others).
Under what circumstances are they invalid?
Where did I say they were invalid? Why are you responding with this? Are you reading what I wrote? You can choose many different synchronizations this doesn't make any of them invalid. You can choose the Einstein Synchronization Convention. However, there is a reason it's called a convention...
Other conventions wouldn't have the one-way speed of light isotropic and we can equally use those conventions. We don't know what simultaneous is (this would require an instantaneous signal) so we can't measure the one-way speed of light without assuming a convention. The problem is we can get any number of an infinite number of answers depending on what convention we use.
Post by: guest39538 on 17/07/2017 01:20:23
If you could do it then you may have something but that's a rather big if. People have been saying they've measured the one-way speed of light independent of a clock synchronization convention for over 100 years but they never have. Amusingly, they attempt to measure this value to defend Einstein's Relativity unnecessarily because it was Einstein who showed that you couldn't.
I do not think measuring the one way speed of light seems that difficult of a thought. I know I could certainly measure the one way speed of light to observe if we have the correct speed of light at the moment of 299792458 m/s. That is a relative simple challenge.
I am sure we could then adjust the experiment in my thoughts of above to measure a true speed if 299792458 m/s was incorrect.
To test the present speed of light one way we can simply use a strobe set to flash once per second. We can then have a detector (radiometer) a set distance away to detect the light.
For example : If the detector was 149896229 m away from the strobe that was flashing 1 flash/second, the detector would detect 2 flashes/second if c is 299792468 m/s
We can calculate the above down to a usable distance then with a bit of ''magic'' , work out the new speed.
added- something like that anyway, I am going fishing in the morning for 4 days so will think about it under the stars and clear up my own thoughts.
Post by: David Cooper on 17/07/2017 16:26:14
To test the present speed of light one way we can simply use a strobe set to flash once per second. We can then have a detector (radiometer) a set distance away to detect the light.
How are you going to time it? Are you going to use one clock or two?
If you use one clock and place it by the strobe unit, how long does it take for the information to get back from the detector to the clock once the light has reached the detector? That signal returns at the speed of light, so you're actually timing the two-way speed of light (i.e. a round trip).
If you use two clocks and have one by the strobe and the other by the detector, you need to synchronise the two clocks, and how do you synchronise them? Any viable method of synchronisation that you use will automatically lead to you measuring the two-way speed of light instead of the one-way speed of light.
Post by: Bored chemist on 17/07/2017 22:28:49
You didn't.Yes, I know I'm making those assumptions (and some others).
Under what circumstances are they invalid?
Where did I say they were invalid?
But, unless there are circumstances where they are invalid then it doesn't matter that I made them.
Pointing out that I'm making an assumption is only worthwhile if that assumption is, or might be, wrong.
So, when would the assumptions I made be wrong?
Also, if they are right from my point of view, the I can measure the one-way speed of light from my point of view.
And, as far as I can tell, it's going to be pretty much the same as the two way speed.
And as far as I understand it, that's the same for everyone.
And there's nothing special about me.
Anyone anywhere could do a similar experiment and get the same answer: in the limit, the measured 1 way speed of light-per this experiment- is C
Post by: guest4091 on 18/07/2017 17:20:46
aka the 2nd postulate.
Let's elaborate on the simultaneity convention.
"That light requires the same time to traverse the same path A to M as for the path B to M is in reality neither a supposition nor a hypothesis about the physical nature of light, but a stipulation which I can make of my own freewill in order to arrive at a definition of simultaneity."
Relativity The Special and the General Theory
Albert Einstein 1961 Crown Publishers Inc. pg 23
aka, physics by decree.
Post by: dutch on 18/07/2017 20:13:43
You didn't.
But, unless there are circumstances where they are invalid then it doesn't matter that I made them.
Pointing out that I'm making an assumption is only worthwhile if that assumption is, or might be, wrong.
Quote
Generalizations of Lorentz transformations with anisotropic one-way speeds
A synchronization scheme proposed by Reichenbach and Grünbaum, which they called ε-synchronization, was further developed by authors such as Edwards (1963),[48] Winnie (1970),[17] Anderson and Stedman (1977), who reformulated the Lorentz transformation without changing its physical predictions.[1][2] For instance, Edwards replaced Einstein's postulate that the one-way speed of light is constant when measured in an inertial frame with the postulate:
The two way speed of light in a vacuum as measured in two (inertial) coordinate systems moving with constant relative velocity is the same regardless of any assumptions regarding the one-way speed.[48]
So the average speed for the round trip remains the experimentally verifiable two-way speed, whereas the one-way speed of light is allowed to take the form in opposite directions:
c± = c / (1 ± κ) where κ is any value between 0 and 1.
As demonstrated by Hans Reichenbach and Adolf Grünbaum, Einstein synchronization is only a special case of a more broader synchronization scheme, which leaves the two-way speed of light invariant, but allows for different one-way speeds. The formula for Einstein synchronization is modified by replacing ½ with ε:[4]
t2 = t1 + ε (t3 - t1)
ε can have values between 0 and 1. It was shown that this scheme can be used for observationally equivalent reformulations of the Lorentz transformation, see Generalizations of Lorentz transformations with anisotropic one-way speeds.
Quote
As required by the experimentally proven equivalence between Einstein synchronization and slow clock-transport synchronization, which requires knowledge of time dilation of moving clocks, the same non-standard synchronizations must also affect time dilation. It was indeed pointed out that time dilation of moving clocks depends on the convention for the one-way velocities used in its formula.[17] That is, time dilation can be measured by synchronizing two stationary clocks A and B, and then the readings of a moving clock C are compared with them. Changing the convention of synchronization for A and B makes the value for time dilation (like the one-way speed of light) directional dependent. The same conventionality also applies to the influence of time dilation on the Doppler effect.[18] Only when time dilation is measured on closed paths, it is not conventional and can unequivocally be measured like the two-way speed of light. Time dilation on closed paths was measured in the Hafele–Keating experiment and in experiments on the Time dilation of moving particles such as Bailey et al. (1977).[19] Thus the so-called twin paradox occurs in all transformations preserving the constancy of the two-way speed of light.
https://en.wikipedia.org/wiki/One-way_speed_of_light#Generalizations_of_Lorentz_transformations_with_anisotropic_one-way_speeds
The formula is:
c± = c / (1 ± κ) where κ is ANY value between 0 and 1.
as κ approaches 1 c- → ∞ which is nowhere near c. Infinity isn't "close to" c.
You didn't.
But, unless there are circumstances where they are invalid then it doesn't matter that I made them.
Pointing out that I'm making an assumption is only worthwhile if that assumption is, or might be, wrong.
It might be wrong, it might be right the point is we CANNOT measure the one-way speed of light independent of a choice of synchronization. You're essentially breaking the Lorentz Transformation into parts and you CANNOT do this. We measure the Lorentz Transform taken as a whole.
The following is true:
t'/t = f'/f = (1 - v/c) / γ where γ = √(1 - (v/c)²) (this is the Lorentz Time Transformation in simplest form)
However, the following is also true:
t'/t = f'/f = (1 - v/c) / γ = γ / (1 + v/c) = (1 - a/c) / (1 + b/c) γb/γa where v = (a + b) / (1 + a b /c²)
Time dilation could be : τ = t / γ or τ = γ t or τ = γb/γa t these are all different. Given a t τ could be 0 to infinity.
We CANNOT measure time dilation τ by any known means. What we can measure in a lab is observed time t' and our time t. We can only measure values locally. No matter what assumptions we make t' and t are symmetric.
Everyone could agree on the two-way speed of light c relative to everything, everyone will agree on t'/t, everyone will agree on f'/f, and defining v by a specific f'/f there's agreement on v. People won't agree on τ and they won't agree on the one-way speed of light UNLESS you force a certain convention. Even then they will seem to contradict because both observers will think the others clock is running slow and both will think light is moving at exactly c relative to them (and from their perspective only for them).
If all you can know is t' and t (really t'/t) you can certainly choose one equation to make your life easier. However, you CANNOT look at individual chunks of that equation like they have some reality beyond your choice of convention. This is the greatest misunderstanding of Relativity. You CANNOT break the Lorentz Transformation into component pieces without making major assumptions. We only measure the input t and the output t'.
It is written, "the measured speed of light is c", A. Einstein.
aka the 2nd postulate.
Let's elaborate on the simultaneity convention.
"That light requires the same time to traverse the same path A to M as for the path B to M is in reality neither a supposition nor a hypothesis about the physical nature of light, but a stipulation which I can make of my own freewill in order to arrive at a definition of simultaneity."
Relativity The Special and the General Theory
Albert Einstein 1961 Crown Publishers Inc. pg 23
aka, physics by decree.
That's Einstein admitting he had formed a convention of his own freewill. It's OK to have a convention as long as people admit it's a convention. He wanted A definition of simultaneity so he could make the math easier. It's a beautiful shortcut that works but we must still acknowledge that we can't measure the one-way speed of light independent of a synchronization convention.
Post by: dutch on 18/07/2017 23:32:39
t'/t = f'/f = (1 - v/c) / γ where γ = √(1 - (v/c)²)
Becomes this:
t' = ( t - v x / c²) / γ (I used the reciprocal of what's normally γ in the last post so the math wouldn't look as messy)
t'/t = (1 - v/c) / γ
= (t - t v/c) / γ
Assume the one-way speed of light is c and synchronize using Einstein Synchronization t = x/c (synchronize clocks with light).
= (t - x/c v/c ) / γ
= ( t - v x / c²) / γ
The equation f'/f = (1 - v/c) / γ is also the Relativistic Doppler shift but so is f'/f = γ / (1 + v/c) and... (side note: the LT and RDS are highly related as they should be)
f'/f = √(1 - v/c) / √(1 + v/c) and f'/f = (1 - a/c) / (1 + b/c) γb/γa for v = (a + b) / (1 + a b /c²)
Why is t'/t = f'/f when f is a frequency of light?
If I send a radio signal out at 10 MHz and someone else receives it at 20 MHz they observe my time at 2 times the normal rate. I can confirm with them and they can send a signal to me from an identical radio. I will receive 20 MHz from their 10 MHz radio keeping the observables symmetric. The ratios of frequency and ratios of time observed must be equal to conserve information. I don't know τ independent of a convention nor can I know the one-way speed of light independent of a convention.
https://en.wikipedia.org/wiki/Doppler_effect
https://en.wikipedia.org/wiki/Relativistic_Doppler_effect
Post by: Bored chemist on 19/07/2017 22:30:41
Then we know that you are not playing by the rules I specified where everyone is walking or cycling round on the surface of the Earth.
Post by: dutch on 20/07/2017 03:04:23
Then we know that you are not playing by the rules I specified where everyone is walking or cycling round on the surface of the Earth.
?
What are you even writing about? I was making a point about the math. The size of the frequency shift doesn't matter to the point whatsoever. You completely missed the point that t' and τ are completely different variables. I don't care if you're "walking or cycling" you still don't know the one-way speed of light without using a clock synchronization convention.
However, I'm glad you're getting your exercise.
I've got questions but let me set the questions up. Say there's a clock positioned at A and another at B when those clocks remain stationary on the surface of the Earth such that one is at sea level (A) and the other (B) 1,000 feet above sea level their reference frame feels acceleration and clock B will run faster than clock A.
Using the Equivalence Principle, I can accelerate two clocks connected by a 1,000 foot steel cable. If I accelerate in the direction of clock B then clock B will run faster when observed by clock A during the acceleration. I can accelerate slow enough such that when I inspect the cable later it will be the same length and in the same condition it originally was. I therefore conclude the length remains 1,000 feet between ships when finished (at least as observed by me). When the acceleration stops clock B will again run at the same rate as observed by clock A (this observed time is t').
If I assume Einstein Clock Synchronization (one-way speed of light is c for my frame) then clocks that were synchronized before the acceleration are now out of sync. However, my clocks remain synchronized to the original reference frame. Therefore, I decide of my own freewill to move either the rear clock's time reading forward or the front clock's time reading backwards to fix the "problem" I perceive based on my convention. I choose to re-synchronize the clocks because I assume the one-way speed of light is constant in my new reference frame. I had assumed the one-way speed of light was constant in my old reference frame but after I choose to re-synchronize my clocks the old assumption is no longer valid. I decided I didn't like my original choice to keep the math simpler.
Questions:
1) Why couldn't I just keep my original clock synchronization? Why do I have to re-synchronize?
2) How is my synchronization not based on convention?
3) If I did attempt to measure the one-way speed of light using my original synchronization it would be different in different directions. If I'm lazy and I keep my original synchronization why is this less valid then re-synchronizing? Why do I have to reset spatially separated clocks after every acceleration? Does nature know that it needs to re-synchronize its clocks after accelerations?
Say you're in a lab that changed velocity by .8c a while ago and the scientists in charge of the lab re-synchronizes the clocks. You measure the one-way speed of light and get exactly c. You get excited thinking you just measured the one-way speed. You also don't realize that the scientist reset the clocks... You attempt to justify the re-synchronization. However, careful analysis of slow clock transport and light synchronization you find that those are identical. To your surprise you go back into the system and restore the original clock settings and the one-way speed of light is 1.8γ² c in one direction and .2γ² c in the other (where γ = √(1 - .8²) = .6 the gamma is due to time dilation/length contraction with respect to the original frame chosen as a reference; also remember v = d/t).
c± = c / (1 ± κ) If κ = .8 then c - = c / (1 -.8 ) = 5c = 1.8γ² c and c+ = c / (1 +.8 ) = 5/9c = .2γ² c (predicted value without resync)
Why is slow clock transport the same as fast clock transport? Take a light clock where every bounce of the light between two mirrors is one tick. As you slowly transport the clock from A to B you realize something amazing... you just sent a light beam from A to B just like light synchronization does. You sent the light in a zigzag pattern but careful analysis of the math shows that it doesn't matter because the light still goes through a net horizontal distance from A to B. ALL clocks will give the exact same result because they are all more alike than people think. We are after all made out of a bunch of sub atomic particles interacting via the fundamental forces. If you don't believe this than careful analysis of experiments proves it (it's an experimentally verified fact). Hell, Quantum Field Theory predicts that particles like electrons, quarks, weak bosons, etc would move at light speed if not for their interaction with the Higgs Field and/or the EM field and/or strong field (forming a rest mass). This interaction doesn't slow down the fundamental two-way speed of their "fields" it just gets them "stuck in the mud" via very complex interactions with other fields. This is often called "self energy." Gravity, the EM field, and the strong force all have a two-way speed c. Careful analysis shows that you quickly start to run out of "slow clock transports" that aren't really "light synchronizations" in disguise. Experiments and Relativity also verifies this fact.
They discuss QFT in this series.
Finally, FYI even tiny changes in velocity like walking or cycling changes the speed of light if you don't re-sync the clocks. We do measure this difference as the speed of light is only c locally in General Relativity (small but measurable). Einstein stipulates that you need to re-synchronize your clocks locally. That is you need to keep re-syncing your clocks after every acceleration so they are temporarily localized. In a gravity field or when under acceleration the speed of light is only c in a small enough volume around every point (spatially localized; how local this needs to be depends on the acceleration/curvature). This is the Law of Physics called Local Lorentz Covariance (the heart of GR and included in all modern mainstream theories). We always can assume a convention where we can measure c locally in all directions.
Post by: guest39538 on 21/07/2017 10:41:12
I am not using any clocks to time it in the above. The strobe flashes 1 flash per second, the detector then detects and the detection of the pulses should be in correlation to the strobe at distance x, if it isn't , then c is not c as it stands at the moment and Maxwell would be wrong . i.e the detects should be 1 second apart.To test the present speed of light one way we can simply use a strobe set to flash once per second. We can then have a detector (radiometer) a set distance away to detect the light.
How are you going to time it? Are you going to use one clock or two?
If you use one clock and place it by the strobe unit, how long does it take for the information to get back from the detector to the clock once the light has reached the detector? That signal returns at the speed of light, so you're actually timing the two-way speed of light (i.e. a round trip).
If you use two clocks and have one by the strobe and the other by the detector, you need to synchronise the two clocks, and how do you synchronise them? Any viable method of synchronisation that you use will automatically lead to you measuring the two-way speed of light instead of the one-way speed of light.
Post by: dutch on 21/07/2017 19:28:15
I am not using any clocks to time it in the above. The strobe flashes 1 flash per second, the detector then detects and the detection of the pulses should be in correlation to the strobe at distance x, if it isn't , then c is not c as it stands at the moment and Maxwell would be wrong . i.e the detects should be 1 second apart.
I already answered this. You're measuring t', t' (and f') are symmetric as required by Relativity as shown below:
Quote
t'/t = f'/f = (1 - v/c) / γ = γ / (1 + v/c) = (1 - a/c) / (1 + b/c) γb/γa where v = (a + b) / (1 + a b /c²)
Time dilation could be : τ = t / γ or τ = γ t or τ = γb/γa t these are all different. Given a t τ could be 0 to infinity.
The one-way speed of light could be measured with values from zero to infinity with the following (depending on synchronization used):
c± = c / (1 ± κ) where κ = 0 to 1
If v = 0 between two objects then f'/f = 1 and t'/t = 1 but so what? No one disputes this fact. Both observers will think the other clock is running at the same rate as their own clock. Receiving light pulses every second IS a light clock... so you are using a clock.
To measure the one-way speed of light independent of a synchronization convention you MUST:
1) Universally prove what now is at two different locations beyond some arbitrary convention.
2) Get clocks A (start) and B (finish) ticking at the same rate in an absolute sense.
For over 100 years and with countless geniuses thinking about the subject the first condition still has not been met. The second condition can be met (have no acceleration/minimal curvature) but it's nowhere near sufficient to measure the one-way speed independent of a convention.
You may know the pulses are 1 second apart BUT you don't know what time the pulses were emitted without relying on a synchronization convention that let's you sync two spatially separated clocks. You MUST start the stop watch at the same absolute time at position A and at position B to measure the speed in an absolute sense. We do NOT have a sense of absolute time. In Relativity absolute time simply doesn't exist so we use a convention to form "planes of simultaneity." In LET absolute time exists but we have no way to identify it because while a rest frame exists in principle no frame is preferred in the math in any experimentally distinguishable way.
Post by: David Cooper on 21/07/2017 22:18:38
I am not using any clocks to time it in the above.
Let me get this straight - you're timing something without using any kind of clock?
Quote
The strobe flashes 1 flash per second, the detector then detects and the detection of the pulses should be in correlation to the strobe at distance x, if it isn't , then c is not c as it stands at the moment and Maxwell would be wrong . i.e the detects should be 1 second apart.
So, you've got a flash every second at the strobe and a flash being detected every second at the detector, so how do you get from there to a measurement of the time taken for the light to get from the strobe to the detector?
Post by: guest39538 on 22/07/2017 10:36:41
At the detector end the received packets should be an equal space apart on the readout, equal to the distance the light as travelling .plus 1 second.I am not using any clocks to time it in the above.
Let me get this straight - you're timing something without using any kind of clock?QuoteThe strobe flashes 1 flash per second, the detector then detects and the detection of the pulses should be in correlation to the strobe at distance x, if it isn't , then c is not c as it stands at the moment and Maxwell would be wrong . i.e the detects should be 1 second apart.
So, you've got a flash every second at the strobe and a flash being detected every second at the detector, so how do you get from there to a measurement of the time taken for the light to get from the strobe to the detector?
My thoughts are still a bit incomplete, but I can visual ''see'' the idea in my head. Maybe I will draw the idea later.
The distance between the strobe and detector would have to be a fraction of the distance of the speed of light, the readout would have to scroll off at a second rate, so many lines per second, then we could do the maths. I am using the scrolling of the readout as my second clock.
added- ok I am going to visualise the experiment in my head, I am know longer looking at the screen so forgive me if my tyoing is rubbish, I now see the strobe and see the first photon emitted, the photon travles across the distance tot he detector which is already in motion, the photon striokes the detector and puts a mark on the graph, The second one comes and strikes a mark oon the graph, I can now use scaled reading to give a result.
detect.jpg (31.83 kB . 1152x648 - viewed 5247 times)added - let us start with the first detect and in example we will say 0.1s, the second detect 1.1s, the third 2.2s and so on .
let us use 3.26cm of distance on the printout to equal 1.s
printout speed = 3.26cm/1.s
We are using an equivalent to measure time and by the comparison can measure speed .
added- No need to worry about synchronous starts either. Turn on the detector , turn on the strobe, get measuring lol
added- obviously if we could get the distance of 299792458m between emit and detect it would be much easier to calculate.
Each flash should be recorded 3.26cm apart , this would equal the present prediction and Maxwell had it right. If not, we can then use the distance difference to get a true speed. Quite elementary really.
<3.26cm = faster
=3.26cm= equal 299792568m/s
>3.26cm = slower
In short we are setting up the experiment to the exact prediction of Maxwell. All results should conform to this, if not then it is quite obvious we are wrong about the speed.
3.26cm /s = 299792458m/s in our scaling.
A photon travels 299792458m compared to a line that travels 3.26cm in the same time.
added- only the first 3 detects are important to give a result.
Post by: guest39538 on 22/07/2017 11:46:00
detect 1.jpg (31.06 kB . 1152x648 - viewed 5313 times)p.s Just elementary my dear Watson , what next Watson? that was too easy ....
p.s don't forget to make your printout machine variable in speed so you can adjust the speed to get a true speed of c if the prediction fails.
Post by: Bored chemist on 22/07/2017 12:20:01
In the limit of a low speed, low acceleration, low gravity situation, we can measure the one-way speed of light to an arbitrarily high accuracy.Then we know that you are not playing by the rules I specified where everyone is walking or cycling round on the surface of the Earth.
?
What are you even writing about? I was making a point about the math. The size of the frequency shift doesn't matter to the point whatsoever. You completely missed the point that t' and τ are completely different variables. I don't care if you're "walking or cycling" you still don't know the one-way speed of light without using a clock synchronization convention.
However, I'm glad you're getting your exercise.
I've got questions but let me set the questions up. Say there's a clock positioned at A and another at B when those clocks remain stationary on the surface of the Earth such that one is at sea level (A) and the other (B) 1,000 feet above sea level their reference frame feels acceleration and clock B will run faster than clock A.
Using the Equivalence Principle, I can accelerate two clocks connected by a 1,000 foot steel cable. If I accelerate in the direction of clock B then clock B will run faster when observed by clock A during the acceleration. I can accelerate slow enough such that when I inspect the cable later it will be the same length and in the same condition it originally was. I therefore conclude the length remains 1,000 feet between ships when finished (at least as observed by me). When the acceleration stops clock B will again run at the same rate as observed by clock A (this observed time is t').
If I assume Einstein Clock Synchronization (one-way speed of light is c for my frame) then clocks that were synchronized before the acceleration are now out of sync. However, my clocks remain synchronized to the original reference frame. Therefore, I decide of my own freewill to move either the rear clock's time reading forward or the front clock's time reading backwards to fix the "problem" I perceive based on my convention. I choose to re-synchronize the clocks because I assume the one-way speed of light is constant in my new reference frame. I had assumed the one-way speed of light was constant in my old reference frame but after I choose to re-synchronize my clocks the old assumption is no longer valid. I decided I didn't like my original choice to keep the math simpler.
Questions:
1) Why couldn't I just keep my original clock synchronization? Why do I have to re-synchronize?
2) How is my synchronization not based on convention?
3) If I did attempt to measure the one-way speed of light using my original synchronization it would be different in different directions. If I'm lazy and I keep my original synchronization why is this less valid then re-synchronizing? Why do I have to reset spatially separated clocks after every acceleration? Does nature know that it needs to re-synchronize its clocks after accelerations?
Say you're in a lab that changed velocity by .8c a while ago and the scientists in charge of the lab re-synchronizes the clocks. You measure the one-way speed of light and get exactly c. You get excited thinking you just measured the one-way speed. You also don't realize that the scientist reset the clocks... You attempt to justify the re-synchronization. However, careful analysis of slow clock transport and light synchronization you find that those are identical. To your surprise you go back into the system and restore the original clock settings and the one-way speed of light is 1.8γ c in one direction and .2γ c in the other (where γ = 1/√(1 - .8²) = 1.67 the gamma is due to time dilation with respect to the original frame chosen as a reference; also remember v = d/t).
c± = c / (1 ± κ) If κ = 2/3 then c - = c / (1 -2/3) = 3c = 1.8γ c and c+ = c / (1 +2/3) = 1/3c = .2γ c (predicted value without resync)
Why is slow clock transport the same as fast clock transport? Take a light clock where every bounce of the light between two mirrors is one tick. As you slowly transport the clock from A to B you realize something amazing... you just sent a light beam from A to B just like light synchronization does. You sent the light in a zigzag pattern but careful analysis of the math shows that it doesn't matter because the light still goes through a net horizontal distance from A to B. ALL clocks will give the exact same result because they are all more alike than people think. We are after all made out of a bunch of sub atomic particles interacting via the fundamental forces. If you don't believe this than careful analysis of experiments proves it (it's an experimentally verified fact). Hell, Quantum Field Theory predicts that particles like electrons, quarks, weak bosons, etc would move at light speed if not for their interaction with the Higgs Field and/or the EM field and/or strong field (forming a rest mass). This interaction doesn't slow down the fundamental two-way speed of their "fields" it just gets them "stuck in the mud" via very complex interactions with other fields. This is often called "self energy." Gravity, the EM field, and the strong force all have a two-way speed c. Careful analysis shows that you quickly start to run out of "slow clock transports" that aren't really "light synchronizations" in disguise. Experiments and Relativity also verifies this fact.
They discuss QFT in this series.
Finally, FYI even tiny changes in velocity like walking or cycling changes the speed of light if you don't re-sync the clocks. We do measure this difference as the speed of light is only c locally in General Relativity (small but measurable). Einstein stipulates that you need to re-synchronize your clocks locally. That is you need to keep re-syncing your clocks after every acceleration so they are temporarily localized. In a gravity field or when under acceleration the speed of light is only c in a small enough volume around every point (spatially localized; how local this needs to be depends on the acceleration/curvature). This is the Law of Physics called Local Lorentz Covariance (the heart of GR and included in all modern mainstream theories). We always can assume a convention where we can measure c locally in all directions.
If you have someone moving WRT us so fast that they perceive our 1 MHz clock as 20MHz then that's a different scenario.
You are plainly better at the maths than I am.
So, calculate the answer to the question I set earlier. If the one way speed of light is the same as C then m will be 10,000.
What value do you calculate (for simplicity assume that C is exactly 300,000,000 m/s, the frame rate is (locally) exactly 1 million frames per second and the separation is exactly million metres.)
I'd expect m to be 10,000.
Post by: dutch on 23/07/2017 02:55:12
In the limit of a low speed, low acceleration, low gravity situation, we can measure the one-way speed of light to an arbitrarily high accuracy.
No, not independent of a clock synchronization which makes the one-way speed of light measurement a two-way speed of light measurement.
If you have someone moving WRT us so fast that they perceive our 1 MHz clock as 20MHz then that's a different scenario.
This simply doesn't matter. Where did I say this mattered? I made an example before to show you how the math works and you completely misunderstood it.
You are plainly better at the maths than I am.
If you don't know the math then you most likely don't understand the argument. From what you've written it appears that you're missing the points and the math. You probably should understand those before asserting anything.
So, calculate the answer to the question I set earlier. If the one way speed of light is the same as C then m will be 10,000.
What value do you calculate (for simplicity assume that C is exactly 300,000,000 m/s, the frame rate is (locally) exactly 1 million frames per second and the separation is exactly million metres.)
I'd expect m to be 10,000.
OK. I don't think your math here is right even if I make your assumptions. The separation should be 3 million meters with your assumptions not 1 million meters. Also you're making the exact same mistake Thebox is making with some of his setups to measure the one-way speed of light. The 10,000 is a frequency measured in Hz. You have a signal of 10 KHz.
Both position A (emitter) and position B (receiver) if their relative velocity is 0 will measure this same frequency of 10 KHz. OK fine, this doesn't tell me when position A emitted a particular flash it only tells me the flashes occur 10,000 times per second. This isn't helpful in measuring the one-way speed of light at all.
Let's slow way down and look at the Classical Doppler Shift:
fmo = f (1 - v) This is the equation for a moving observer.
fms = f / (1 + v) This is the equation for a moving source. Please note v is a value between -1 and 1 (velocity negative is towards observer and positive is away from observer).
for a moving source and observer fmso = f (1 - a) / (1 + b) (combining the two equations)
Say you've got a long train and you've got a locomotive in the back and front (pusher and puller). These locomotives have train whistles and the train is moving at a velocity of .1.
If f = 1,000 then what frequency would the locomotive in the back see?
Well to get this value it's simple. The emitting locomotive in the front is a source moving away and the locomotive in the back is the observer moving towards:
fmso = f (1 - a) / (1 + b) = 1000 ( 1 - (-.1))/(1 + .1) =1000 * 1.1/1.1 = 1000
The rear locomotive is moving at the same velocity as the front locomotive so the frequency does NOT change.
Likewise the following occurs if the locomotive in the front observes the whistle from the rear.
fmso = f (1 - a) / (1 + b) = 1000 ( 1 - .1)/(1 + (-.1)) =1000 * .9/.9 = 1000
Again the frequency does not change.
However, if the rear train whistle emits a noise it moves forward at a velocity of .9 because the train is moving at .1. The other sound moves rearward at 1.1.
The sound moving rearward reaches the rear locomotive FASTER than the sound moving toward the forward locomotive. However, the frequency does NOT shift.
How do we know the sounds travel at different speeds going forwards and backwards? Well, we can because sound isn't the fastest thing we could use to send a message. We can use light signals to notify the front locomotive of when the rear locomotive fired its whistle. We can then use light to more accurately set our clocks than sound. Light is simply much closer to instantaneous than sound so its a better option to synchronize clocks (light moves so fast it gives us an existence where we think we know what "now" is at different locations). We can definitely tell that the rear whistle must fire much earlier than the front whistle in order for the observers to receive the sounds at the same time as synchronized by light. The rear whistle must fire earlier if a light signal can be sent informing the front locomotive that the rear locomotive fired its whistle.
HOWEVER, light does not move instantaneous and it's actually infinitely far from instantaneous (light speed is finite). It's true it's much better than sound to synchronize times but it's still highly limited. The Relativistic Doppler Shift doesn't add anything more to this argument.
We can tell one locomotive emitted a sound earlier than another within our setup because we can use something faster than sound to synchronize. However, what can we use that's faster than light? NOTHING (ever seen). The math I wrote already explained the concepts behind all of this.
Post by: Bored chemist on 23/07/2017 11:00:29
Let's clarify what I consider to be synchronisation.
I get two "clocks"
They are boxes with a button marked "zero" and a display on the front that is a number. It continuously counts "microseconds since someone pushed the zero button".
They are both "perfect" clocks. If you set them up next to each other the difference between the two displays will always be the same.
If you press the "zero" buttons on both at the same time then the displays will count up in synchrony.
At the start of the experiment I set both clocks to zero by pressing the "zero" buttons on both at the same time.
(I have to say that I thought we could assume that, rather than having to spell it out).
Since the two cameras take a picture a million times a second, each frame is effectively "numbered" by the picture of the clock.
Since each pair (a clock and a camera) are always kept together and they are "perfect" they will remain synchronised to one-another.
Now, just as a sense check, I can do a thought experiment where I repeat the "clock on a plane" trial.
I take one clock and it's camera and fly them round the world on a jet plan.
When they get home, I can compare them and I see that the moving clock no longer agrees with the clock that stayed at home (from my POV).
Do you agree so far that there's a difference between what the two clocks say?
(for a trip on a plane round the world the difference is too small to see on a microsecond scale, but that's OK, I can set the clocks and cameras to record nanoseconds instead. I lke thought experiments- they are so much cheaper).
If I repeated the original Hafele–Keating experiment the disparities measured would be much the same as they measured.
-59 ns one way and 273 ns the other.
Do we agree so far?
OK.
Now the clocks are back home I re-synchronise them (locally) by pressing both buttons at the same time.
And I get on my bike with one pair and ride off 3000 km into the distance (I'm assuming the Earth is flat for this experiment).
I put the clock + camera down and I ride home again. (Again, I'm glad this is just a thought experiment).
For the sake of having some numbers, I set off, and accelerate to 3 m/sec linearly over the course of 10 seconds then I maintain exactly the same speed until I get near the end, and I then decelerate linearly over 10 sec to zero .
I set of a flash bulb (it's a very short very bright flash).
I stop the nearby clock and camera and look at the recording.
The flash appears on frame n.
I get back on my (t)rusty bike and set off to the other camera.
I look through that recording and I find that the flash appears on frame n+m
What value do you predict for m?
For convenience of arithmetic I's saying that C is exactly 300,000,000 m/s so the time it takes to cover the distance of 3 km is 1/100 seconds.
And with a million frames a second, m should be 10,000
But obviously, that's ignoring any relativistic effects.
How big are those effects?
By how much does m differ from 10,000 ?
(I don't mind if it's a fraction- in principle, we can just speed the clocks up and make it a big enough integer to count reasonable accurately)
And I'm going to keep asking the same question until I get an answer of the form "m=10000.0001 " or whatever or a request to clarify some aspect of the experimental procedure.
Post by: David Cooper on 23/07/2017 21:06:09
[Because a clock's ticking rate slows more dramatically the faster it is moved through space, moving the clocks more quickly to the ends of the ship will lead to both of them lagging further behind the middle clock, but the lag will be the same for both. You will therefore get different times from them by changing the speeds of relocation, but despite this, both the northern and southern clock will always agree on the time taken for a signal to reach them from the middle clock.]
Post by: Bored chemist on 23/07/2017 21:12:17
If I'm on a spaceship moving through space at high speed in a direction which we'll call "north" (for want of a better word), I can go to the middle of the ship and synchronise three clocks there. I can then send two of the clocks to the ends of the ship (one to each) such that we now have three synchronised clock spaced apart with one perhaps 50m to the north of the middle one and another 50m to the south of the middle one. By moving the clocks in this way though, their synchronisation has actually changed - the southern clock's time is running ahead of the other two, and the northern clock is lagging most (but they are back to ticking at the same rate as each other). If I now send a signal from the middle clock to the other two, both those clocks will record the same time of arrival even though the signal takes longer to reach the northern clock.That's a nice story.
[Because a clock's ticking rate slows more dramatically the faster it is moved through space, moving the clocks more quickly to the ends of the ship will lead to both of them lagging further behind the middle clock, but the lag will be the same for both. You will therefore get different times from them by changing the speeds of relocation, but despite this, both the northern and southern clock will always agree on the time taken for a signal to reach them from the middle clock.]
Do you have an opinion on the value of m in the experiment I suggested?
Post by: guest39538 on 23/07/2017 23:19:02
If I'm on a spaceship moving through space at high speed in a direction which we'll call "north" (for want of a better word), I can go to the middle of the ship and synchronise three clocks there. I can then send two of the clocks to the ends of the ship (one to each) such that we now have three synchronised clock spaced apart with one perhaps 50m to the north of the middle one and another 50m to the south of the middle one. By moving the clocks in this way though, their synchronisation has actually changed - the southern clock's time is running ahead of the other two, and the northern clock is lagging most (but they are back to ticking at the same rate as each other). If I now send a signal from the middle clock to the other two, both those clocks will record the same time of arrival even though the signal takes longer to reach the northern clock.no, you are measuring time by counting at different speeds which is wrong.
[Because a clock's ticking rate slows more dramatically the faster it is moved through space, moving the clocks more quickly to the ends of the ship will lead to both of them lagging further behind the middle clock, but the lag will be the same for both. You will therefore get different times from them by changing the speeds of relocation, but despite this, both the northern and southern clock will always agree on the time taken for a signal to reach them from the middle clock.]
Post by: David Cooper on 23/07/2017 23:20:33
That's a nice story.
Do you have an opinion on the value of m in the experiment I suggested?
I would have if I could be bothered doing the maths, but it's more important for you to realise that if you use the same method to put an identically synchronised clock+camera the same distance away in the opposite direction, the timing you get from it will always match up with the other measurement you make in the first direction, so you clearly aren't going to be able to measure the one-way speed of light unless you happen to be stationary relative to the fabric of space by luck.
Post by: David Cooper on 23/07/2017 23:24:56
no, you are measuring time by counting at different speeds which is wrong.
I'm discussing synchronising three clocks at a single location, then moving two of them away in opposite directions and using these synchronised clocks to time a signal sent at the speed of light from the middle clock to the outer two. The clocks are all counting at the same speed as each other, but they weren't doing so while two of them were being relocated.
It's important to point out though that if you repeat the process many times moving the synchronised clocks from the centre into position more and more slowly, the lag between them will get smaller and smaller each time you do it. This tends towards zero lag (assuming that the central clock is at rest relative to the fabric of space). You can get directly to zero lag by better synchronisation methods, so we're really discussing an extremely poor method of clock synchronisation here.
Post by: guest39538 on 23/07/2017 23:31:38
no, you are measuring time by counting at different speeds which is wrong.
I'm discussing synchronising three clocks at a single location, then moving two of them away in opposite directions and using these synchronised clocks to time a signal sent at the speed of light from the middle clock to the outer two. The clocks are all counting at the same speed as each other, but they weren't doing so while two of them were being relocated.
The clocks are never out of synchronisation if the clock is being used correctly i.e 1=1
I understand the distance contractions/expansions would cause an issue in timing, sorry I thought you were trying to still say there was a time dilation.
Post by: David Cooper on 23/07/2017 23:55:45
The clocks are never out of synchronisation if the clock is being used correctly i.e 1=1
If you move one clock relative to another, you will necessarily push them out of synchronisation - the only issue is how much, with faster speeds of movement pushing them out of sync by more.
Quote
I understand the distance contractions/expansions would cause an issue in timing, sorry I thought you were trying to still say there was a time dilation.
Moving a clock slows its ticking. If you want to drag length-contraction in too, then it reduces the slowing of the ticking (by making it the same no matter which way the clock is aligned), but you still have slowed ticking while the clock's moving.
Post by: guest39538 on 24/07/2017 00:53:34
But all the slowed ticking means is the timing mechanism is out of synchronisation, there is no actual physical length contraction, there is just more or less distance the light has to travel fromThe clocks are never out of synchronisation if the clock is being used correctly i.e 1=1
If you move one clock relative to another, you will necessarily push them out of synchronisation - the only issue is how much, with faster speeds of movement pushing them out of sync by more.QuoteI understand the distance contractions/expansions would cause an issue in timing, sorry I thought you were trying to still say there was a time dilation.
Moving a clock slows its ticking. If you want to drag length-contraction in too, then it reduces the slowing of the ticking (by making it the same no matter which way the clock is aligned), but you still have slowed ticking while the clock's moving.
or 
. This in no way affects the rate of time it affects the rate of timing. It is not much difference to when a timing belt slips and a car misfires. The clocks only become out of synchronisation because they are not very good clocks.
Post by: Bored chemist on 24/07/2017 10:46:10
Aha!The clocks are never out of synchronisation if the clock is being used correctly i.e 1=1
If you move one clock relative to another, you will necessarily push them out of synchronisation - the only issue is how much, with faster speeds of movement pushing them out of sync by more.
Progress!
Imagine that I repeat the thought experiment I did earlier (the one where I was carrying a clock round on a bicycle).
I repeat it several times, but I use different modes of transport..
With a space ship, the difference between the "expected" value for m and 10,000 is larger tan when I use a jet plane.
And that, in turn is bigger than when I use a bike.
The version where I uses continental drift to move the clocks gives a result even closer to 10,000.
So, I can measure the 1 way speed of light by extrapolation of the speed as I move the clocks slower.
In the limit I can calculate it for moving the clocks at zero speed.
Is there any reason to suppose that, if I did that, the limiting value I would get for the 1 way speed of light was any different from C?
Post by: GoC on 24/07/2017 11:54:29
So, I can measure the 1 way speed of light by extrapolation of the speed as I move the clocks slower
When you move a clock it is not measuring the speed of light. It is measuring the distance light travels through space. Speed does not matter on the Earth from the continental drift to a light beam. All clocks tick at the same rate at sea level. Simultaneity of relativity does not consider time of movement a factor. Frequency of light does not change the speed of light but it does affect the tick rate of a clock. This affect causes clocks to measure distance indirectly as simultaneity of relativity.
Post by: Bored chemist on 24/07/2017 12:14:49
When you move a clock it is not measuring the speed of light.How fortunate, then, that nobody said it was. Why did you raise the issue?
Measuring the speed of light is when I measure the time it takes for light to travel through a known distance- from 1 clock to the other.
"All clocks tick at the same rate at sea level."
Moving ones don't.
That's the whole damned point.
Post by: GoC on 24/07/2017 12:27:22
Measuring the speed of light is when I measure the time it takes for light to travel through a known distance- from 1 clock to the other."All clocks tick at the same rate at sea level."Moving ones don't.That's the whole damned point.
Of course. But speed between clock positions does not affect the difference in reading on the moved clock.
Post by: guest39538 on 24/07/2017 12:32:07
Simultaneity of clocks at rest in an inertia reference frames is directly related to the mass of the inertia reference frame. If m1 is different to m2, the clocks on m1 and m2 will tick differently. I consider this is all simultaneity is .So, I can measure the 1 way speed of light by extrapolation of the speed as I move the clocks slower
When you move a clock it is not measuring the speed of light. It is measuring the distance light travels through space. Speed does not matter on the Earth from the continental drift to a light beam. All clocks tick at the same rate at sea level. Simultaneity of relativity does not consider time of movement a factor. Frequency of light does not change the speed of light but it does affect the tick rate of a clock. This affect causes clocks to measure distance indirectly as simultaneity of relativity.
Post by: Bored chemist on 24/07/2017 13:38:41
But speed between clock positions does not affect the difference in reading on the moved clock.
the only issue is how much, with faster speeds of movement pushing them out of sync by more.
Post by: David Cooper on 24/07/2017 17:09:32
If we move the clocks out more slowly, we allow them to tick while they're moving, and the slower we move them out to their destinations, the less far behind they will lag in their ticking behind the central clock, but there will always be a lag. The two outer clocks will be synchronised with each other though without any such lag, so that should give you a clue as to a better method for synchronising clocks - if you're using two of them, you have to move both of them in opposite directions the same distance and at the same speed.
If you can get that idea into your head, the next thing to consider is what happens the system isn't stationary. When you move the clocks apart, one of them may be moving faster through space than the other, so that means it will tick more slowly than the other while they're being moved into position from the central point. That adjusts the synchronisation. We can still do this with three clocks so that we keep a central clock which never accelerated. The faster we move the clocks apart, the further out of sync the central clock will be with the outer two, but we can work out how to correct for that to remove that additional lag for the outer clocks, thereby getting them all to the same synchronisation they would have if we had somehow been able to move the clocks apart infinitely slowly. The clocks are not in sync though, because the one that moved fastest through space lags behind the other two, and the clock that moved the opposite way will be ahead of the other two with its timings (after the correction has been made either to the central clock or the two outer clocks). This difference in synchronisation will guarantee that when you use these synchronised clocks (which will only be displaying the same time simultaneously if the system is stationary), your attempted measurement of the one-way speed of light will always produce the answer c regardless of the actual speed of light relative to the system.
Post by: GoC on 24/07/2017 18:06:25
Imagine three clocks that are sitting together. They are wired together and connected to a button which can be used to synchronise them all.
That is impossible if you understand relativity.
If we move the clocks out more slowly, we allow them to tick while they're moving, and the slower we move them out to their destinations, the less far behind they will lag in their ticking behind the central clock, but there will always be a lag. The two outer clocks will be synchronised with each other though without any such lag, so that should give you a clue as to a better method for synchronising clocks - if you're using two of them, you have to move both of them in opposite directions the same distance and at the same speed.
Are we in the solar system? How fast is the solar system spinning? Are we in a galaxy? How fast is the galaxy spinning? Are you going with the spin or against the spin? How do you determine not moving?
The clocks are not in sync though, because the one that moved fastest through space lags behind the other two,
Your clock is a measure of distance by distance. One light second distance from rest no matter how fast or how slow will register one second difference. The electron in your clock measures the distance in reduction of tick rate due to further distance for the constant electron to travel through. Electron distance is confounded with the distance the light goes through.
Post by: David Cooper on 24/07/2017 20:21:04
Imagine three clocks that are sitting together. They are wired together and connected to a button which can be used to synchronise them all.
That is impossible if you understand relativity.
If you happen to be moving through space at 99.9999c there will be a big synchronisation error as the clocks can never quite be in a single location no matter how close together you put them, but this will be a trivial error compared with the synchronisation differences once the clocks have been moved apart. For this reason, it is generally considered possible to synchronise two (or more) clocks at a single location.
Quote
Are we in the solar system? How fast is the solar system spinning? Are we in a galaxy? How fast is the galaxy spinning? Are you going with the spin or against the spin? How do you determine not moving?
Bored chemist referred to a flat world to eliminate such problems from his scenario. He could alternatively have put the system in deep space. If you're working in a lab though and only want to move the clocks from the middle to the ends of the room, any rotations of the lab are unimportant so long as the clocks are always aligned on a straight line. If you want to work on the Earth's surface and move the clocks thousands of miles apart, you can't going to end up with all three clocks in a straight line, so you can't do the synchronisation this way. It's a good idea though if you understand the difficulties of synchronising clocks on a straight line first before you start trying to understand the extra complications of moving them round a curved surface of a spinning object.
Quote
The clocks are not in sync though, because the one that moved fastest through space lags behind the other two,
Your clock is a measure of distance by distance. One light second distance from rest no matter how fast or how slow will register one second difference. The electron in your clock measures the distance in reduction of tick rate due to further distance for the constant electron to travel through. Electron distance is confounded with the distance the light goes through.
Does what you've said negate what I said in some way? Two clocks moved in opposite directions, but one was moving faster through space, so its asserted time lags behind that of the other clock.
Post by: Bored chemist on 24/07/2017 21:50:57
Imagine three clocks that are sitting together. They are wired together and connected to a button which can be used to synchronise them all. We press the button, then we send two of the clocks away in opposite directions. If the central clock is not moving through space, the other two clocks will tick more slowly as they are moved through space. TheBox doesn't seem to understand this point, but if you move the clocks at the speed of light they will stop functioning completely while they're being moved, so if you move them one lightsecond of distance away and then leave them there, the two clocks that you've moved will start ticking again, but they're both one second behind the central clock. The two outer clocks are synchronised with each other, but they're not synchronised any more with the central clock.I can get it into my head just fine that your plan to synchronise the clocks won't work because there is a delay (typically the product of the square root of dielectric constant of the insulation on the wires and the distance divided by c IIRC).
If we move the clocks out more slowly, we allow them to tick while they're moving, and the slower we move them out to their destinations, the less far behind they will lag in their ticking behind the central clock, but there will always be a lag. The two outer clocks will be synchronised with each other though without any such lag, so that should give you a clue as to a better method for synchronising clocks - if you're using two of them, you have to move both of them in opposite directions the same distance and at the same speed.
If you can get that idea into your head,
So you are not actually synchronising the clocks with the one in the middle- we know there's a delay.
The delay may well be the same in each direction but, as you can reduce it to zero by moving them slowly...
Adding a 3rd clock doesn't really seem to add anything.
Re " if you move the clocks at the speed of light they will stop functioning completely while they're being moved, "
Then don't.
Why choose the state of affairs where the error you introduce is as big as possible?
Why not move them slowly so they stay (arbitrarily close to) synchronised?
Post by: David Cooper on 24/07/2017 23:18:06
I can get it into my head just fine that your plan to synchronise the clocks won't work because there is a delay (typically the product of the square root of dielectric constant of the insulation on the wires and the distance divided by c IIRC).
How are you synchronising them then when you have two clocks together? Are you pressing buttons on both of them and getting an error of up to a tenth of a second instead of using one button to start both? I can assure you that my way of doing it is more accurate. The big question though is about getting clocks synchronised at a distance and the errors that necessarily find their way into that, so the trivial business of how synchronising clocks at a single location is done is a trivial sideshow.
Quote
So you are not actually synchronising the clocks with the one in the middle- we know there's a delay.
The delay may well be the same in each direction but, as you can reduce it to zero by moving them slowly...
Adding a 3rd clock doesn't really seem to add anything.
I brought the third clock into this to try to help you see how awful your synchronisation method is. If you synchronise the three clocks at the central location, you can then move two of them away from there in opposite directions at the same speed to get them where you want them to be. Those two clocks are now as just about as well synchronised with each other as they can be, but only if the system happens to be stationary rather than moving fast through space. The middle clock though is badly synchronised with them, and the faster you moved the other two clocks into position, the worse the synchronisation with the middle clock will be. You only have two clocks, and one of them is being treated like my middle clock, so you're getting the huge error in your synchronisation instead of the minimal error with my two outer clocks. If you know how fast you moved your moving clock relative to your stationary clock though, you can adjust the timing of one or other of them to correct that synchronisation, at which point your clocks can be just as well synchronised as my pair of moved clocks. In both cases though, even that superior synchronisation will be affected by the movement of the system through space, so one clock's time may be far ahead of the other, which is why when you use them to attempt to measure the one-way speed of light, you are guaranteed to get the value c regardless of the actual speed of the light that you're timing relative to the system.
Quote
Re " if you move the clocks at the speed of light they will stop functioning completely while they're being moved, "
Then don't.
Imagine a light clock aligned with the direction you're moving it in. If you move this clock at c, the clock will stop clicking throughout the time you're moving it because the light would have to travel faster than c in order to complete a circuit (and thereby to tick). All clocks are limited in the same way, slowed to the same extent by their movement through space.
Quote
Why choose the state of affairs where the error you introduce is as big as possible?
Why not move them slowly so they stay (arbitrarily close to) synchronised?
The faster you move your only moved clock into position, the sooner you can start using your clocks to make measurements. It would be stupid to take a million years to move your clock into position just to minimise a predictable error which you can simply adjust for. That error is a complication which you want to eliminate, and it's a diversion away from the nature of the real error that you cannot correct for - the undetectable error affects all methods of synchronisation and it affects them equally. It's caused by the communication delay in one direction being longer than in the opposite direction if the system is moving through space.
Post by: guest39538 on 25/07/2017 01:18:01
Quote from: David
Imagine three clocks that are sitting together. They are wired together and connected to a button which can be used to synchronise them all. We press the button, then we send two of the clocks away in opposite directions. If the central clock is not moving through space, the other two clocks will tick more slowly as they are moved through space. TheBox doesn't seem to understand this point,
Of course I understand this point and I also understand this point to be incorrect which you do not.
Let me take three light clocks ,
the distance between the mirrors on clock one is a Planck length .
the distance between the mirrors on clock two is 1 mm
the distance between the mirrors on clock three is 1cm
Oh look I have just created different tick rates by adding distance the light has to travel between ticks.
Let us start again and measure time correctly.
I have again 3 light clocks,
the distance between the mirrors on clock one is a Planck length .
the distance between the mirrors on clock two is a Planck length
the distance between the mirrors on clock three is a Planck length
Oh look we are now synchronous
Sorry for being ''cocky'' David, but quite clearly you do not understand relative correctness.
Post by: David Cooper on 25/07/2017 17:10:33
Quote from: DavidImagine three clocks that are sitting together. They are wired together and connected to a button which can be used to synchronise them all. We press the button, then we send two of the clocks away in opposite directions. If the central clock is not moving through space, the other two clocks will tick more slowly as they are moved through space. TheBox doesn't seem to understand this point,
Of course I understand this point and I also understand this point to be incorrect which you do not.
The "this point" in the bit you've quoted points forwards to the rest of the content of the same sentence where the point is made much more clearly for you - if you could move the clocks at the speed of light, they would stop ticking altogether (while being moved). If you move them at a little bit less than the speed of light they may struggle to complete a single tick while being moved. The slower you move them, the more quickly they will tick while being moved, but they will always be ticking more slowly than the stationary clock while they are moving. I've shown you the proof of this a multitude of times in another thread and you stubbornly refuse to accept it, even though you seemed to agree with every step of the argument along the way, so it's entirely a matter of you having a belief which you are not prepared to part with no matter how much it is shown to be wrong, and there's no fix for that.
Quote
Let me take three light clocks ,
the distance between the mirrors on clock one is a Planck length .
the distance between the mirrors on clock two is 1 mm
the distance between the mirrors on clock three is 1cm
Oh look I have just created different tick rates by adding distance the light has to travel between ticks.
And moving a clock will increase the communication distances too.
Quote
Let us start again and measure time correctly.
I have again 3 light clocks,
the distance between the mirrors on clock one is a Planck length .
the distance between the mirrors on clock two is a Planck length
the distance between the mirrors on clock three is a Planck length
Oh look we are now synchronous
And now you've just introduced a length-contraction much stronger than the one that everyone else accepts, and you've added a width-contraction to it too! But you won't recognise that because you're a magical thinker.
Quote
Sorry for being ''cocky'' David, but quite clearly you do not understand relative correctness.
If you base your physics in magic, that's entirely up to you, but it means you're just one more artist making Turner-Prize-winning works out of elephant dung.
Post by: guest39538 on 25/07/2017 18:02:47
Quote from: DavidImagine three clocks that are sitting together. They are wired together and connected to a button which can be used to synchronise them all. We press the button, then we send two of the clocks away in opposite directions. If the central clock is not moving through space, the other two clocks will tick more slowly as they are moved through space. TheBox doesn't seem to understand this point,
Of course I understand this point and I also understand this point to be incorrect which you do not.
The "this point" in the bit you've quoted points forwards to the rest of the content of the same sentence where the point is made much more clearly for you - if you could move the clocks at the speed of light, they would stop ticking altogether (while being moved). If you move them at a little bit less than the speed of light they may struggle to complete a single tick while being moved. The slower you move them, the more quickly they will tick while being moved, but they will always be ticking more slowly than the stationary clock while they are moving. I've shown you the proof of this a multitude of times in another thread and you stubbornly refuse to accept it, even though you seemed to agree with every step of the argument along the way, so it's entirely a matter of you having a belief which you are not prepared to part with no matter how much it is shown to be wrong, and there's no fix for that.QuoteLet me take three light clocks ,
the distance between the mirrors on clock one is a Planck length .
the distance between the mirrors on clock two is 1 mm
the distance between the mirrors on clock three is 1cm
Oh look I have just created different tick rates by adding distance the light has to travel between ticks.
And moving a clock will increase the communication distances too.QuoteLet us start again and measure time correctly.
I have again 3 light clocks,
the distance between the mirrors on clock one is a Planck length .
the distance between the mirrors on clock two is a Planck length
the distance between the mirrors on clock three is a Planck length
Oh look we are now synchronous
And now you've just introduced a length-contraction much stronger than the one that everyone else accepts, and you've added a width-contraction to it too! But you won't recognise that because you're a magical thinker.QuoteSorry for being ''cocky'' David, but quite clearly you do not understand relative correctness.
If you base your physics in magic, that's entirely up to you, but it means you're just one more artist making Turner-Prize-winning works out of elephant dung.
Quote
if you could move the clocks at the speed of light, they would stop ticking altogether
And this means nothing except there is nothing to count. Quite clearly my ''magic'' is much more objective than your Myths.
Science is adding a length to contract when there is no length there to begin with. Time does not move in 1 second jumps, it moves continuous at the smallest rate we can understand time Planck. You carry on believing the subjective thought, the belief you have not being factual.
You are ignorant by the way, you do not want to understand or try to understand.
Post by: dutch on 25/07/2017 18:39:50
Please read the following from Stanford University on this matter. Also note that the burden of proof falls on those who wish to prove the non-conventionality of synchronization.
https://plato.stanford.edu/entries/spacetime-convensimul/
If you can't synchronize clocks without using a convention, then you CANNOT measure the one-way speed of light without circularly referring to that convention. If you can't prove one convention explains more than another (as in verifiable predictions) then all remain valid... regardless of opinion.
But all the slowed ticking means is the timing mechanism is out of synchronisation, there is no actual physical length contraction, there is just more or less distance the light has to travel from or . This in no way affects the rate of time it affects the rate of timing. It is not much difference to when a timing belt slips and a car misfires.
Really? No physical length contraction? Prove it to me.......
Aha!
Progress!
Imagine that I repeat the thought experiment I did earlier (the one where I was carrying a clock round on a bicycle).
I repeat it several times, but I use different modes of transport..
With a space ship, the difference between the "expected" value for m and 10,000 is larger tan when I use a jet plane.
And that, in turn is bigger than when I use a bike.
The version where I uses continental drift to move the clocks gives a result even closer to 10,000.
So, I can measure the 1 way speed of light by extrapolation of the speed as I move the clocks slower.
In the limit I can calculate it for moving the clocks at zero speed.
Is there any reason to suppose that, if I did that, the limiting value I would get for the 1 way speed of light was any different from C?
That's not progress... If two objects accelerate off in opposite directions from one central point by the same amount they will have symmetric Doppler Shifts to the original position. This will have a very real and verifiable effect (symmetric Doppler Shifts verified by central observer). It doesn’t matter what m is in your experiment. When the two clocks go back to a speed of v=0, m could be many values depending on synchronization chosen. Two objects could have their clocks synchronized and they could blast off in opposite directions at 90% the speed of light in the same way relative to their initial location then they stop. Their clocks are STILL SYNCHRONIZED with their initial reference frame if they didn't re-sync (if you use Einstein Synchronization). Sure, their clocks may have ticked at different rates than a clock left at their initial location, but this has no bearing on the problem whatsoever. You could pick any other reference frame to synchronize to and the physics works the same. That we need to have ε =1/2 is a human made condition AKA a convention. The clocks may only tick at 43.5% during their journey but they would still have the same reading relative to each other using the original reference frame throughout the journey (via Einstein Synchronization).
All other ε are used in Relativity (see the Lorentz Transformation) why do they have to pertain to "other" reference frames? Why does a mile need to be 5,280 feet? Why do some countries drive on the left while others drive on the right? Why do we have to use a base 10 number system? These are all conventions. We could have physics where ε =1/4 or 1/8 but we chose 1/2.
If you move one clock relative to another, you will necessarily push them out of synchronization - the only issue is how much, with faster speeds of movement pushing them out of sync by more.
No, you can accelerate two synchronized clocks from the same location in opposite directions with the same amount of acceleration. You can then decelerate the clocks back so their velocities relative to their initial location is zero. These clocks don't need to be re-synchronized relative to the original frame (assuming they were not re-synced during the trip). Their original synchronization assumed Einstein Synchronization convention and their initial and final velocities are the same. Under acceleration clocks i a moving frame get out of sync with respect to their final reference frame but remain synchronized with the original reference frame (assuming Einstein Clock Synchronization). If the final velocity matches the initial velocity and the trips were symmetric then with the standard convention the clocks may have run slow but they ran slow by the same amount. While the trip is symmetric from the original frame’s view it certainly isn’t from all other reference frames.
The clocks only become out of synchronisation because they are not very good clocks.
Really? Find me better clocks then.
no, you are measuring time by counting at different speeds which is wrong.
What? Why?
Post by: guest39538 on 25/07/2017 18:52:01
What? Why?
Time moves forward directly proportional to the history created at an infinite speed/rate. Count as fast as you can and see if you can count faster than time passes by.
It does not matter if you count time past slow or fast, the time passes by immediately always.
Post by: David Cooper on 25/07/2017 20:57:05
If you move one clock relative to another, you will necessarily push them out of synchronization - the only issue is how much, with faster speeds of movement pushing them out of sync by more...
No, you can accelerate two synchronized clocks from the same location in opposite directions with the same amount of acceleration.
Which is exactly what I've already explained in earlier posts. If you move one clock relative to another (which it was at rest with and which continues to be unaccelerated), they will go out of sync.
Importantly, if you could move the clocks away from the central location to their new equally distant locations in opposite directions at the speed of light, you would have set up your synchronisation at a distance in the shortest possible time, and we can get the same result in the real universe by sending out synchronisation signals at the speed of light from a central location.
You can also synchronise two clocks by sending a light signal from one to the other and then making the adjustment for the delay in getting light to travel the known distance (by the clocks' rest frame's measurement), so there is no need for anyone to go to the midway point.
You can also synchronise two clocks where you don't know the distance between them by timing the round trip of a light signal to calculate the distance, but that will take twice as long to do (on average).
The simplest way to understand the synchronisation of clocks issue though is to play tennis between the two clocks, sending signals back and forth. The first clock will send a signal and start its clock at 0, then the second clock will start its clock at 1 when it receives the signal. The first clock will reset its clock to 2 when it gets a signal back and it will recalibrate the rate of its timing to tie in with that figure so that it will read 4 when the next signal arrives. The second clock resets its clock to 3 when it receives a second signal and it recalibrates its timing to tie in with the length of the delay such that it will read 5 when the next signal arrives. (These counts are unlikely to be seconds, but they could be used internally while a display in seconds is provided instead.) Importantly though, each clock ticks at regular intervals with one on the even numbers when the signal arrives and the other on the odd numbers. If the clocks are both at rest, both will tick the same number at the same instant. If they are moving, the leading clock will tick late, but it will always tick before the trailing clock makes its tick for the next value. What we have set up is essentially a light clock with one end in each of our two locations.
Post by: Bored chemist on 25/07/2017 22:16:23
OK, these are those nice clocks you find in thought experiments.I can get it into my head just fine that your plan to synchronise the clocks won't work because there is a delay (typically the product of the square root of dielectric constant of the insulation on the wires and the distance divided by c IIRC).
How are you synchronising them then when you have two clocks together? Are you pressing buttons on both of them and getting an error of up to a tenth of a second instead of using one button to start both? I can assure you that my way of doing it is more accurate. The big question though is about getting clocks synchronised at a distance and the errors that necessarily find their way into that, so the trivial business of how synchronising clocks at a single location is done is a trivial sideshow.QuoteSo you are not actually synchronising the clocks with the one in the middle- we know there's a delay.
The delay may well be the same in each direction but, as you can reduce it to zero by moving them slowly...
Adding a 3rd clock doesn't really seem to add anything.
I brought the third clock into this to try to help you see how awful your synchronisation method is. If you synchronise the three clocks at the central location, you can then move two of them away from there in opposite directions at the same speed to get them where you want them to be. Those two clocks are now as just about as well synchronised with each other as they can be, but only if the system happens to be stationary rather than moving fast through space. The middle clock though is badly synchronised with them, and the faster you moved the other two clocks into position, the worse the synchronisation with the middle clock will be. You only have two clocks, and one of them is being treated like my middle clock, so you're getting the huge error in your synchronisation instead of the minimal error with my two outer clocks. If you know how fast you moved your moving clock relative to your stationary clock though, you can adjust the timing of one or other of them to correct that synchronisation, at which point your clocks can be just as well synchronised as my pair of moved clocks. In both cases though, even that superior synchronisation will be affected by the movement of the system through space, so one clock's time may be far ahead of the other, which is why when you use them to attempt to measure the one-way speed of light, you are guaranteed to get the value c regardless of the actual speed of the light that you're timing relative to the system.QuoteRe " if you move the clocks at the speed of light they will stop functioning completely while they're being moved, "
Then don't.
Imagine a light clock aligned with the direction you're moving it in. If you move this clock at c, the clock will stop clicking throughout the time you're moving it because the light would have to travel faster than c in order to complete a circuit (and thereby to tick). All clocks are limited in the same way, slowed to the same extent by their movement through space.QuoteWhy choose the state of affairs where the error you introduce is as big as possible?
Why not move them slowly so they stay (arbitrarily close to) synchronised?
The faster you move your only moved clock into position, the sooner you can start using your clocks to make measurements. It would be stupid to take a million years to move your clock into position just to minimise a predictable error which you can simply adjust for. That error is a complication which you want to eliminate, and it's a diversion away from the nature of the real error that you cannot correct for - the undetectable error affects all methods of synchronisation and it affects them equally. It's caused by the communication delay in one direction being longer than in the opposite direction if the system is moving through space.
You can synchronise them however you like, including the button on the top.
If they are next to each other then here's an amusing way to do it.
Turn one of the clocks upside down.
Press its button down on the button of the other clock.
Since both presses are the same event they are necessarily synchronised exactly.
But that's not the point.
It's a thought experiment we don't worry about irrelevant issues like whether my reflexes are good enough to press two buttons in a tenth of a second or what.
Because the two clocks are next to each other it's perfectly simple to synchronise them. Relativity doesn't have any problems with "at the same time" for things that are "in the same place".
Now, do you see that my "awful" synchronisation method is (at the time when I'm synchronising them) actually mathematically perfect?
You can see how no observer anywhere in the universe, regardless of their speed, acceleration of local gravity will ever see the two clocks -just after I push both buttons in the same place and at the same time- as being anything other than synchronised?
Synchronous is hard in GR.
It can only happen locally.
That's why I choose to set the clocks running at zero in the same place and at the same time.
From the point of view of nearly everybody else in the universe, your "synchronised clocks" are ( or at least may be) never in step because they are separate in space.
With my approach, once we have two clocks that at least start out together we can run the experiment where we know how far out of synch the clocks are (because we can calculate it from the way in which we moved one of them).
And we can minimise that change.
We can make it as mall as we like (by moving them a short distance and/ or slowly).
And then we have two nearly synchronised clocks which we can set off a flash lamp in front of and look at the delay.
Post by: David Cooper on 25/07/2017 23:23:40
OK, these are those nice clocks you find in thought experiments.
You can synchronise them however you like, including the button on the top.
If they are next to each other then here's an amusing way to do it.
Turn one of the clocks upside down.
Press its button down on the button of the other clock.
Since both presses are the same event they are necessarily synchronised exactly.
Try doing that with three clocks, but you've also got the problem that the buttons probably won't "fire" simultaneously, so you're really going to have to smash the clocks together hard to minimise the error.
Quote
It's a thought experiment we don't worry about irrelevant issues like whether my reflexes are good enough to press two buttons in a tenth of a second or what.
Then stop obsessing about it - the reason I spelt out a reasonable method was to attempt to ward off any ridiculous diversions of the kind that have subsequently been taken.
Quote
Because the two clocks are next to each other it's perfectly simple to synchronise them. Relativity doesn't have any problems with "at the same time" for things that are "in the same place".
You're repeating what I've already said.
Quote
Now, do you see that my "awful" synchronisation method is (at the time when I'm synchronising them) actually mathematically perfect?
You can see how no observer anywhere in the universe, regardless of their speed, acceleration of local gravity will ever see the two clocks -just after I push both buttons in the same place and at the same time- as being anything other than synchronised?
That's not the part of the synchronisation process that I'm calling awful. The awful part is when you move one of them somewhere else and it's movement slows it and leads to its timing lagging by a different amount depending on how quickly you relocated it.
Quote
That's why I choose to set the clocks running at zero in the same place and at the same time.
From the point of view of nearly everybody else in the universe, your "synchronised clocks" are ( or at least may be) never in step because they are separate in space.
With my approach, once we have two clocks that at least start out together we can run the experiment where we know how far out of synch the clocks are (because we can calculate it from the way in which we moved one of them).
And we can minimise that change.
There are better methods where you don't have to worry about extra errors creeping in from the way you accelerate and decelerate your moving clock, plus complications from little wanders off a straight path vertically and horizontally. You can simply send a flash of light.
Quote
We can make it as small as we like (by moving them a short distance and/ or slowly).
Which you don't need to do as you still have to make a correction, so you might as well make a big correction and move the clock quickly.
Quote
And then we have two nearly synchronised clocks which we can set off a flash lamp in front of and look at the delay.
And at the end of it all, when you time the delay, you get the answer c because you have synchronised clocks with the same time difference between them as with any other valid method so that they will assert the speed is c even if it's actually close to 0 or 2c.
Post by: Bored chemist on 26/07/2017 14:19:07
OK, these are those nice clocks you find in thought experiments.
You can synchronise them however you like, including the button on the top.
If they are next to each other then here's an amusing way to do it.
Turn one of the clocks upside down.
Press its button down on the button of the other clock.
Since both presses are the same event they are necessarily synchronised exactly.
Try doing that with three clocks, but you've also got the problem that the buttons probably won't "fire" simultaneously, so you're really going to have to smash the clocks together hard to minimise the error.QuoteIt's a thought experiment we don't worry about irrelevant issues like whether my reflexes are good enough to press two buttons in a tenth of a second or what.
Then stop obsessing about it - the reason I spelt out a reasonable method was to attempt to ward off any ridiculous diversions of the kind that have subsequently been taken.QuoteBecause the two clocks are next to each other it's perfectly simple to synchronise them. Relativity doesn't have any problems with "at the same time" for things that are "in the same place".
You're repeating what I've already said.QuoteNow, do you see that my "awful" synchronisation method is (at the time when I'm synchronising them) actually mathematically perfect?
You can see how no observer anywhere in the universe, regardless of their speed, acceleration of local gravity will ever see the two clocks -just after I push both buttons in the same place and at the same time- as being anything other than synchronised?
That's not the part of the synchronisation process that I'm calling awful. The awful part is when you move one of them somewhere else and it's movement slows it and leads to its timing lagging by a different amount depending on how quickly you relocated it.QuoteThat's why I choose to set the clocks running at zero in the same place and at the same time.
From the point of view of nearly everybody else in the universe, your "synchronised clocks" are ( or at least may be) never in step because they are separate in space.
With my approach, once we have two clocks that at least start out together we can run the experiment where we know how far out of synch the clocks are (because we can calculate it from the way in which we moved one of them).
And we can minimise that change.
There are better methods where you don't have to worry about extra errors creeping in from the way you accelerate and decelerate your moving clock, plus complications from little wanders off a straight path vertically and horizontally. You can simply send a flash of light.QuoteWe can make it as small as we like (by moving them a short distance and/ or slowly).
Which you don't need to do as you still have to make a correction, so you might as well make a big correction and move the clock quickly.QuoteAnd then we have two nearly synchronised clocks which we can set off a flash lamp in front of and look at the delay.
And at the end of it all, when you time the delay, you get the answer c because you have synchronised clocks with the same time difference between them as with any other valid method so that they will assert the speed is c even if it's actually close to 0 or 2c.
"Try doing that with three clocks, "
As far as I can tell, the only thing you do with the 3rd clock (the one in the middle) is use it to tell you when to sync the other two.
It serves no purpose.
So, I will save myself the trouble of using 3 clocks- one of which does nothing- by just using two.
Also, if you consider an ant sat on one of the two "moving" clocks in your scenario, he sees almost exactly the scenario I use.
He sees the other clock being carried off into the distance.
However there's an important difference.
From his perspective you never synchronise the clocks.
The way I do it, everyone agrees that, when I push the two buttons the two events are simultaneous (because I use one to push the other, so it's a single event and a lack of simultaneity would require a violation of causality)
"but you've also got the problem that the buttons probably won't "fire" simultaneously,"
No, that's why I made it clear that this was a thought experiment with ideal clocks.
"Then stop obsessing about it "
I'm not. You are the one who is going on about the mechanics of pushing two buttons.
"- the reason I spelt out a reasonable method was to attempt to ward off any ridiculous diversions of the kind that have subsequently been taken."
My ant disagrees with your idea of "reasonable".
From his point of view, your "reasonable" method never actually makes the clocks read the same time.
"You're repeating what I've already said."
Well, yes and no.
I keep on pointing out that you can't meaningfully sync two clocks unless they are together- because otherwise, just about everybody else in the universe will never see the two clocks reading the same time.
And you keep saying that you can synchronise them when they are far apart- which is "true" from one unusual point of view- you have to be half way between them.
And then you say this method - which everybody in the universe except you agrees doesn't actually make the clocks tell the same time- is better than mine where everybody does agree that they (initially) say the same time.
That's an odd use of "better".
On the subject of repeating what someone said, I cited the "2 clocks on a jet plane" fairly early in this thread. And then you post "Imagine a light clock aligned with the direction you're moving it in. If you move this clock at c, the clock will stop clicking throughout the time you're moving it because the light would have to travel faster than c in order to complete a circuit (and thereby to tick). All clocks are limited in the same way, slowed to the same extent by their movement through space."
Well, yes, I know that moving clocks makes them run slow. That's why I cited the most famous demonstration of the fact.
Why did you bother to raise it?
"That's not the part of the synchronisation process that I'm calling awful. The awful part is when you move one of them somewhere else and it's movement slows it and leads to its timing lagging by a different amount depending on how quickly you relocated it."
Well, two points there.
The synchronisation process happens with the clocks stationary (and next to each-other) which is the only way you can do it in order that everyone agrees that they are in sync.
So the " part of the synchronisation process that I'm calling awful" isn't part of the synchronisation process .
So there's the second phase where we move a clock.
"The awful part is when you move one of them somewhere else and it's movement slows it and leads to its timing lagging by a different amount depending on how quickly you relocated it."
And the bit that you steadfastly ignore is that you can easily make that error as small as you like.
Why is it that you can say "lagging by a different amount depending on how quickly you relocated it." without realising that, precisely by changing how quickly you relocate it, you can change the lag?
Why not change it to make it as near to zero as you like?
Why not change it, measure the apparent 1 way speed of light, and then extrapolate to the lag that you would get if you moved the clock at zero speed?
Also re "You can simply send a flash of light."
OK, you send a flash of light from the "middle" to start two clocks, then you send a second flash to stop them..
Either you send the second flash from the same place as you send the first- in which case you don't learn anything, or you move between setting off the 2 flashes.
But if you move, time is distorted for you- so you no longer know "when" you are setting off the 2nd flash.
If, from this new position you looked at the 2 clocks, they would no longer be synchronised. The one near you would seem to be running fast compared to the one further away.
You have called this "better".
Do you see why I don't agree?
Post by: dutch on 26/07/2017 18:51:39
And the bit that you steadfastly ignore is that you can easily make that error as small as you like.
No... this is where you go wrong. This depends on the value of ε used and the total desynchronization for a given ε is proportional to the distance x.
If you get two clocks closer together the maximum amount of time the clocks can be out of sync by must decrease for a particular ε but then so does the total round trip time a light beam needs to go from point A to point B (to preserve the two-way speed of light). Regardless of the ε used the clocks go out of sync depending on distance x. You can see this in the Lorentz Transformation below:
t' = γ (t - v x /c²)
Decreasing x by factor a but then decreasing t by factor a preserves the velocity x/t = v = (a x) / (a t). It doesn't matter that the total desynchronization gets smaller as x gets smaller because x gets smaller proportionally. Remember we are measuring a velocity.
You can't measure the one-way speed of light.
1) Using light to synchronize would defeat the purpose of using something else to measure the one-way speed of light (forcing a two-way measurement because you cheated when you used light).
2) Even going a micron or a nano meter in one direction gets clocks out of sync in proportion to the distance meaning you need to re-synchronize the clocks via some synchronization convention. This defeats the purpose of performing a one-way measurement. How much the clocks are out of sync depends on ε and is bounded by the verifiable two-way speed of light c.
3) Slowly transporting clocks in two directions from a central point IS equivalent to measuring the two-way speed of light and does not measure the one-way speed of light. This assumes a certain ε.
Post by: Bored chemist on 26/07/2017 19:45:48
No... this is where you go wrong.Well, I'm copying it from David's post.
I did try to clarify this earlier, but it was ignored.
Post by: Bored chemist on 26/07/2017 19:46:08
OK, so which of these is true?But speed between clock positions does not affect the difference in reading on the moved clock.the only issue is how much, with faster speeds of movement pushing them out of sync by more.
Post by: David Cooper on 26/07/2017 21:12:45
"Try doing that with three clocks, "
As far as I can tell, the only thing you do with the 3rd clock (the one in the middle) is use it to tell you when to sync the other two.
It serves no purpose.
The three clocks are all set to zero. The point of using 3 clocks is to contrast two synchronisation methods - your method uses the middle clock and one of the clocks taken away from it. The alternative method which I was showing you was to take two of the clocks away from the middle one in opposite directions at the same speed and you can do away with the middle clock. With the second method there is no adjustment needed afterwards, but the real purpose of it is to show you that the end result is the same as you get from sending a signal at the speed of light from the middle to the two outer locations and use that to synchronise the clocks. I was trying to show you the equivalence of all the methods and the reason they fail to allow you to determine the one-way speed of light relative to the clocks.
Quote
"Then stop obsessing about it "
I'm not. You are the one who is going on about the mechanics of pushing two buttons.
The history of events is written this thread and it shows that you are the one obsessing by fixating on little details and taking diversions. If I add little details to avoid attacks from people who want to fasten on any imagined errors that result from incomplete description, you don't need to fixate on those details - you are free to stick to the main path and ignore anything that you consider superfluous.
Quote
I keep on pointing out that you can't meaningfully sync two clocks unless they are together- because otherwise, just about everybody else in the universe will never see the two clocks reading the same time.
There are two kinds of synchronisation involved in this discussion. Synchronisation of clocks at a single location doesn't lead to disputes about whether or not they're synchronised other than for nitpickers who want to obsess about details as to how this is done, and if I make a suggestion en passent about how I would synchronise them in this situation (by using one button rather than three), that isn't an invitation for anyone to take a ruddy great diversion over that issue by suggesting I should use a more primitive, less acccurate method for doing it and then attack me for sparking off their ridiculous diversion.
Quote
And you keep saying that you can synchronise them when they are far apart- which is "true" from one unusual point of view- you have to be half way between them.
And this synchronisation is the second type where you synchronise clocks at a distance. This is equivalent to synchronising them together and then moving them apart, which means you do not have a superior method but are merely proposing a less accurate one.
Quote
And then you say this method - which everybody in the universe except you agrees doesn't actually make the clocks tell the same time- is better than mine where everybody does agree that they (initially) say the same time.
That's an odd use of "better".
Your method of synchronising clocks (the second kind where the aim is to have them synchronised and at a distance) is more clumsy and error-prone. Your initial synchronisation (of the first kind) doesn't last after you've started to move them apart, so it's nothing to boast about - you end up with the second kind of synchronisation where the clocks aren't necessarily synchronised any more, but you're also creating extra work for yourself because you have to cancel out an additional error which gives you a lot more work to do (and which you naively wanted to do by moving one clock extremely slowly which wouldn't completely remove the error).
Quote
On the subject of repeating what someone said, I cited the "2 clocks on a jet plane" fairly early in this thread. And then you post "Imagine a light clock aligned with the direction you're moving it in. If you move this clock at c, the clock will stop clicking throughout the time you're moving it because the light would have to travel faster than c in order to complete a circuit (and thereby to tick). All clocks are limited in the same way, slowed to the same extent by their movement through space."
Well, yes, I know that moving clocks makes them run slow. That's why I cited the most famous demonstration of the fact.
I must apologise to you for misreading a reply of yours that led to that - where you wrote "then don't" I read it as "they don't".
Quote
Why did you bother to raise it?
To illustrate the equivalence between moving the clocks out and sending a signal at the speed of light and show you the futility of your attempt to measure the one-way speed of light. That is the issue in question in this thread and I am trying to help you understand why what you think can be done can't.
Quote
"That's not the part of the synchronisation process that I'm calling awful. The awful part is when you move one of them somewhere else and it's movement slows it and leads to its timing lagging by a different amount depending on how quickly you relocated it."
Well, two points there.
The synchronisation process happens with the clocks stationary (and next to each-other) which is the only way you can do it in order that everyone agrees that they are in sync.
So the " part of the synchronisation process that I'm calling awful" isn't part of the synchronisation process .
You're using a synchronisation process which starts with synchronisation of two clocks at a single location and then moves on to a second step which changes that synchronisation to create a synchronisation at a distance (which is a different kind of synchronisation because it doesn't necessarily mean they are ticking at the same time any more). And the thing that makes it most awful is that you think it's a good idea to move one of the clocks really slowly in order to minimise the extra error that you're introducing instead of just moving it fast and making a bigger correction.
Quote
And the bit that you steadfastly ignore is that you can easily make that error as small as you like.
Why is it that you can say "lagging by a different amount depending on how quickly you relocated it." without realising that, precisely by changing how quickly you relocate it, you can change the lag?
I'm fully aware that you can change the degree of lag and have told you so, but why do you want to do that when it means taking ages to set up your clocks and still leaves you with an error anyway? It's as easy to correct for a big error as a small one, so just move your clock fast.
Quote
Why not change it to make it as near to zero as you like?
Why not change it, measure the apparent 1 way speed of light, and then extrapolate to the lag that you would get if you moved the clock at zero speed?
I don't care how you want to do it - that's entirely up to you. I just want you to see the equivalence of the different methods (which is the whole point of showing you them) in the hope that you'll understand that your synchronisation will be no different apart from having extra errors added to it which you will need to adjust for.
Quote
Also re "You can simply send a flash of light."
OK, you send a flash of light from the "middle" to start two clocks, then you send a second flash to stop them..
Either you send the second flash from the same place as you send the first- in which case you don't learn anything...
The whole point is that you can't learn anything about the one-way speed of light.
Quote
You have called this "better".
Do you see why I don't agree?
Yes - I can see why you don't agree, and it's because you're still not seeing the big picture. The error that you're getting in the second kind of synchronisation can be corrected for and there is nothing to gain from moving your clock slowly other than to minimise an error that you can't be bothered adjusting for. Because you actually can be bothered adjusting for it though (because you want to do things with precision), you might as well move the clock fast and save yourself a lot of time. And if you're just doing a thought experiment, if you move two clocks the same distance at c in opposite directions you can eliminate a lot of the maths. You then realise that you can't use your clocks to determine the one-way speed of light if you do that, but you also realise that this method of synchronisation is equivalent to yours and that your way of doing things won't be able to determine the one-way speed of light either. That is all I'm trying to help you see, and looking at these other approaches should help you to get your head around why the different methods are equivalent.
There is one major point on which I may have been wrong, and that's the idea that slower movement leads to less error if you're moving one clock away from another, so I will now think it through again right here and write as I do so. If I move a clock at c a distance d in one second, that clock will lag behind the other by one second because it will stop ticking for a whole second. If I move a clock at 0.5c the same distance d in two seconds, the clock will tick at 87% of its rest ticking rate throughout the move, so it will lag the other by 2x0.13 of a second which is 0.26 of a second. In both cases the clock has moved d, but the lag is not the same. The error that dutch is talking about clearly can't be about this kind of lag (which we can adjust for), so he must be talking about the error that remains after the correction for this lag has been made, and that error (which could be a negative lag for the moved clock) applies regardless of which synchronisation method is used.
Post by: Bored chemist on 26/07/2017 21:28:19
Thanks.
Can you do that for a few more speeds and then plot a graph of "error in clock" vs speed of travel.
Then, we can extrapolate and see what the error is in the limit of zero speed.
If, as I suspect, it turns out to be zero then; for the very odd case of a very simple, slow, system, we can show that the error in the clock synchronisation is smaller than we need to worry about.
so that gives us two clocks that were synchronised and which now have a small, known phase shift. and which are separated in space which we can then use to time the arival of a flash of light as it gets to each of them.
To an arbitrary accuracy we then know the distance and the time (for this weirdly simple system.
Then we can show (fairly easily by the carts you have been putting before the horse) that it won't work in any more complex system- i.e. anywhere in the real world.
Post by: dutch on 26/07/2017 23:16:34
There is one major point on which I may have been wrong, and that's the idea that slower movement leads to less error if you're moving one clock away from another
Yes, that major point is you're assuming (without realizing it) Einstein Synchronization (ε =1/2). You can't assume Einstein Synchronization (speed of light is c in all directions) to prove the speed of light is c in all directions because that's the assumption of Einstein Synchronization. It's completely circular logic. This is especially true when there are other ε you could use which work perfectly fine and c isn't the same in all directions.
Slow clock transport (transporting a clock as slow as possible) is identical mathematically to light synchronization. Using light synchronization to measure the one-way speed of light is cheating (it's a two-way measurement)...therefore so is slow clock transportation. This is easily shown via careful analysis of a slow clock transport of a tiny light clock (light bouncing between two closely spaced mirrors).
Post by: David Cooper on 26/07/2017 23:53:36
Can you do that for a few more speeds and then plot a graph of "error in clock" vs speed of travel.
Then, we can extrapolate and see what the error is in the limit of zero speed.
I told you earlier that this lag tends to zero as you move the clock more slowly, but if you want a way of calculating it for different speeds, just use a calculator to work out the arcsine of the speed expressed in terms such that c = 1, 0.5c = 0.5, etc, (arcsine might be typed in as inv sin) then you need to work out the cosine of the result to get the rate at which the clock will tick while it's moving. You can multiply that by 100 to turn it into a percentage if that helps you understand the answer better.
Quote
If, as I suspect, it turns out to be zero then; for the very odd case of a very simple, slow, system, we can show that the error in the clock synchronisation is smaller than we need to worry about.
Yes, but it'll mean a very slow journey, and whatever speed you move the clock at, you might as well just make an adjustment to remove that lag error anyway. I go back to my system with three clocks - two of them are moved apart in opposite directions at the same speed. If they are moved extremely slowly, the amount they lag behind the middle clock will be small, and if we correct for the speed we moved the clocks out at we can eliminate that lag altogether, so we have three clocks ticking in sync with that lag completely gone. And yet they are not necessarily in sync, and it's a lot easier to explain why this should be the case if we stick to using my three clocks.
If the system is at rest and we move two of the clocks away from the middle one at the same speed in opposite directions, both are slowed. We can correct for that slowing and end up with all three clocks ticking in sync. But, what happens if the system is actually moving? If when we move the two clocks out, it's possible that the middle clock is actually moving throughout and that one of the clocks which we think we're moving away from it is actually at rest in space while we are "moving" it. The opposite clock will be moving twice as fast through space as the middle clock. What happens now is that the time dilation on the fastest moving clock is more than twice as severe as the time dilation acting on the middle clock, so we're warping the synchronisation and have one clock (the one that was stationary when we thought we were moving it) ticking ahead of the middle clock and the clock at the opposite end is ticking behind the middle clock and by a greater degree of lag. When we make the correction to the timings of the two clocks that we "moved" away from the central clock, what happens? We add the missing time back onto them, at which point we increase the lead in ticking of the clock that was already ahead of the middle clock, and we decrease the lag in ticking of the opposite end clock, and the result is that the clock that's ticking ahead of the middle clock is ahead by the same amount as the opposite end clock is ticking behind the middle clock.
No matter how slowly you move the clocks, this final error in the synchronisation will still occur and be the same size for all speeds of movement, which is why dutch says that the size of the error is proportionate to the distance the clocks are moved and not to the speed at which they are moved. He is talking about this residual error and has yet to grasp that we have been talking primarily about a greater error which can be cancelled out and which is bigger the faster you move the clocks. Most importantly though, there is no zero speed of movement for the clocks as that will not separate them, so you will have to move them at some non-zero speed, and no matter how low you make that speed, the same residual error will build up in the synchronisation.
Post by: David Cooper on 27/07/2017 00:09:45
There is one major point on which I may have been wrong, and that's the idea that slower movement leads to less error if you're moving one clock away from another
Yes, ...
No - I demonstrated that I had not been wrong on that point. Read carefully what I said in the post before this one in my latest reply to BC and then you'll hopefully be able to see that we're talking about two different kinds synchronisation error, the bigger of which comes into play when you only move one of the clocks and which is greater the faster you move that clock into place. So far, you appear to have missed the existence of this larger error.
Post by: dutch on 27/07/2017 02:44:44
No - I demonstrated that I had not been wrong on that point. Read carefully what I said in the post before this one in my latest reply to BC and then you'll hopefully be able to see that we're talking about two different kinds synchronisation error, the bigger of which comes into play when you only move one of the clocks and which is greater the faster you move that clock into place. So far, you appear to have missed the existence of this larger error.
Absolutely not. Slow clock transport and light synchronization are identical mathematically as I've said many times. I've actually shown the math on this more than once in this thread but nobody actually bothers with understanding the math I wrote...
Dependent on the original synchronization convention you may think clocks slowly transported are in sync and the total error relative to a light signal used to synchronize will be practically nil. You can even readjust for clocks transported at 50% light speed and resync because you are basing your measurement on your initial convention. This will allow for very accurate measurements of the one-way speed of light but alas ONLY based on your choice of convention. After choosing a convention time dilation doesn't add any error that can't be corrected for exactly (GPS does this all the time). To measure the one-way speed of light at all a convention must be chosen (to know the time dilation at all a convention must be chosen).
The "amount of error" is dependent on your initial synchronization convention. That original convention assumes a value for ε. I already gave links to all of this and quite a bit of math. All I get back is tons of text with no addressing the math.
He is talking about this residual error and has yet to grasp that we have been talking primarily about a greater error which can be cancelled out and which is bigger the faster you move the clocks.
No. You are not writing about a greater error. You can't even "know the error" the way you describe without assuming a convention. The assumed synchronization convention is not a residual error. It's NOT an error at all but rather a choice of convention done because either nothing more exists to find for this or we can't find it because it doesn't matter in any experiment we've ever done. In either case the one-way speed of light is based on convention used.
What exactly are we trying to measure here? The thing you keep calling a "residual error." Extra errors (which can be corrected for anyway when a convention is chosen) caused by crazy ways to transport clocks be damned. I do NOT care about them because the deeper problem is the assumed synchronization we already have. Everything after this is just piling gravy on the already fat chicken.
So far, you appear to have missed the existence of this larger error.
Perhaps maybe you missed the extra fat chicken.
Post by: Bored chemist on 27/07/2017 11:14:05
But can we go back to the system I described?
That way we can ignore (for the minute- we can get back to it later) David's point about "But, what happens if the system is actually moving? ".
We can ignore it because I'm sat here on the ground, looking at the clocks and, from my POV they are not moving.
I am not, for the minute, concerned about how it looks to someone flying past in a plane or whatever.
In that case, I can sync two clocks next to each-other.
I can move one of them away- as slowly as I like, in order to reduce the dime dilation it experiences.
And I can then have two clocks that I know are in synchrony, at least from my point of view- and I don't care about anyone else's (at least for the time being).
And I can use those two clocks and two video cameras to record the time at which the light from a flash bulb reaches them.
And I can measure the distance between the clocks (again, noting that I'm stationary WRT to them so Fitzgerald contraction doesn't enter into it).
I can measure the time it takes for a flash of light to cover a known distance.
From my point of view in this idealised system.
Things will, of course, be different for someone flying past it at half C.
So what?
I'm interested in measuring it here, locally, where gravity is small and even so it has no significant effect (and, at a pinch I could correct for it, but it's easier to just make that correction very small). Round here the change in gravity- if I sent the light straight up- would be about 1 in 10^15 over a distance of 22.5 metres and that's far enough to get a reasonable measurement with modern kit)
(Based on this)
https://en.wikipedia.org/wiki/Pound%E2%80%93Rebka_experiment
If I send the light out horizontally, the effect is much smaller- so I'm going to ignore it.
Where's the problem? I have numbered the steps so you can point out where the issue lies.
(1) Because the clocks are started at the same time in the same place there is no argument about their synchronicity at that point.
(2) Because we move one of them slowly, the phase error on it is arbitrarily small.
So it will stay arbitrarily close to synchronised.
(3) I can measure the distance I move it- again, as slowly as I like.
(4) I can set the cameras to record the clock in the foreground and the flash in the background.
(5) I can analyse the recordings.
(6) I can look record at the time on the clock when the flash arrives.
(7) I can calculate the speed as distance divide by the time difference.
Which step is giving us the problem.
As far as I can tell it's (2).
But, if we move the clock slowly, any relativistic effects are small (as David helpfully did the calculations for - thanks for that).
At the least, we ought to be able to get a good approximation to the 1 way speed of light.
(And if some passing spaceman doesn't agree- what of it? He and I won't even agree on the speed of the number 9 bus; why would we expect his assessment of the 1 way speed of light to be the same as mine?)
Post by: David Cooper on 27/07/2017 16:42:29
Absolutely not. Slow clock transport and light synchronization are identical mathematically as I've said many times. I've actually shown the math on this more than once in this thread but nobody actually bothers with understanding the math I wrote...
It's clear that you don't bother to read text carefully enough to understand what people are saying, so you end up arguing at cross-purposes with them. If you move a light clock at c, it stops ticking throughout the time you're moving it. If you move it at 0.5c it ticks at a slowed rate, 87% of its rest ticking rate - not 50%. At 0.5c it takes twice as long to move the clock into position, but it doesn't miss the same number of ticks while moving as a clock which is moved at c. In both cases there a large error has built up, but we can calculate what that error is (on the mistaken basis that the system is stationary - that's where your convention comes in) and correct for it, and it's only then that we have a remaining error that's proportional to the distance travelled (regardless of the speed the clock was moved). The rest of us have been talking about the error that varies with the speed the clock is moved and which we can correct for, although in making that correction, we naively assume that the system is stationary and therefore we set it up to measure the one-way speed of light as c.
Quote
The "amount of error" is dependent on your initial synchronization convention. That original convention assumes a value for ε. I already gave links to all of this and quite a bit of math. All I get back is tons of text with no addressing the math.
If you expect people to plough through your maths when you can't be bothered to read through our text to find out what we're actually saying, you're going to find yourself starting arguments all over the place with people who agree with you.
Quote
No. You are not writing about a greater error. You can't even "know the error" the way you describe without assuming a convention. The assumed synchronization convention is not a residual error. It's NOT an error at all but rather a choice of convention done because either nothing more exists to find for this or we can't find it because it doesn't matter in any experiment we've ever done. In either case the one-way speed of light is based on convention used.
It almost always is an error - the error is the result of your assumed synchronisation convention, and it's only not an error if the system happens to be at rest in space rather than moving. Of course, if you're doing SR and deny that there is an absolute frame, you can then deny that there's ever an error and call it an infinitely-thin chicken instead, but it's a good idea to start off explaining things in relation to an absolute frame before bringing in that kind of magical complication.
Quote
What exactly are we trying to measure here? The thing you keep calling a "residual error." Extra errors (which can be corrected for anyway when a convention is chosen) caused by crazy ways to transport clocks be damned. I do NOT care about them because the deeper problem is the assumed synchronization we already have. Everything after this is just piling gravy on the already fat chicken.
I don't care about crazy ways to transport clocks either, but BC needs to understand what happens with his chosen way of synchronising clocks, and he isn't going to be fobbed off with answers which only explain other methods.
Post by: guest4091 on 27/07/2017 16:59:31
Absolutely not. Slow clock transport and light synchronization are identical mathematicallyAssuming a Master clock, and 2 Slave clocks, wouldn't the loss of time for the s-clock in slow transport be equal to d/a[1-sqrt(1-a*a)]? d=distance, a=speed
Post by: David Cooper on 27/07/2017 17:11:55
That's all very nice.
But can we go back to the system I described?
The system you described is covered by my three clocks - your system only uses the middle clock and one of the clocks that is moved away from it.
Quote
That way we can ignore (for the minute- we can get back to it later) David's point about "But, what happens if the system is actually moving? ".
We can ignore it because I'm sat here on the ground, looking at the clocks and, from my POV they are not moving.
I am not, for the minute, concerned about how it looks to someone flying past in a plane or whatever.
I'm not concerned about what it looks like to other observers either, but about what the universe thinks of it. If you assume you aren't moving, your experiment will measure the speed of light from one clock to the other as c. If you assume you are moving at 50% the speed of light in the direction you're sending your flash of light, you will make a correction to one of your clocks to cancel out the error you think needs to be applied to it and then you will measure the speed of light to be 0.5c. You're trying to avoid making such a correction because you think the error can be so close to zero that it won't matter, but it's only going to be close to zero if the system's at rest.
Quote
I'm interested in measuring it here, locally, where gravity is small and even so it has no significant effect (and, at a pinch I could correct for it, but it's easier to just make that correction very small). Round here the change in gravity- if I sent the light straight up- would be about 1 in 10^15 over a distance of 22.5 metres and that's far enough to get a reasonable measurement with modern kit)
(Based on this)
https://en.wikipedia.org/wiki/Pound%E2%80%93Rebka_experiment
If I send the light out horizontally, the effect is much smaller- so I'm going to ignore it.
You were talking earlier about doing the experiment horizontally on a flat Earth, so it is equivalent to doing it in deep space. Gravity needn't be considered.
Quote
Where's the problem? I have numbered the steps so you can point out where the issue lies.
The problem is that you're assuming that you're stationary and synchronising your clocks on that basis (and by that, I'm referring to synchronisation at a distance which is forced on your clocks as you move one away from the other).
Quote
(2) Because we move one of them slowly, the phase error on it is arbitrarily small.
So it will stay arbitrarily close to synchronised.
That's where you're going wrong, because the error is only tending to zero if the system is at rest in space. If the stationary clock is actually moving at high speed in the direction you move the other clock, the clock that you move will be moving faster than the "stationary" clock and the time dilation difference will tune your synchronisation in such a way that you end up measuring the speed of light as c regardless of its actual speed relative to the clocks.
I did actually make a mistake in my analysis though. When I had a moving central clock and my other two clocks were moving away from it, one of them was actually at rest during that process and the other was moving twice as fast as the middle clock. But it wouldn't actually be moving twice as fast as the middle clock because it would merely appear that way to an observer at rest with the middle clock, so it may not be undergoing a slowing of its ticking greater than twice the slowing of the middle clock. However, we certainly must have one of the end clocks ticking fastest while the opposite end clock is ticking slowest (during the phase where we're moving them apart), and that will certainly lead to one of the outer clocks lagging behind the middle clock and the middle clock lagging behind the other outer clock. If you are only using the middle clock and one of the outer clocks (while ignoring the other), how do you know which outer clock you're using? Are you using the one that's lagging behind the ticking of the middle clock or are you using the one that the middle clock is lagging behind? You should be able to see from this that there's a skew in the system which is caused by the movement of the system through space while you moved your clock, and that has tuned your synchronisation in such a way that you will measure the speed of light between your clocks as c.
Post by: dutch on 27/07/2017 19:16:56
Quote from: dutch on Today at 02:44:44
Absolutely not. Slow clock transport and light synchronization are identical mathematically
Assuming a Master clock, and 2 Slave clocks, wouldn't the loss of time for the s-clock in slow transport be equal to d/a[1-sqrt(1-a*a)]? d=distance, a=speed
Slow clock transport is the limit as a goes to zero. Given an initial synchronization convention (such as Einstein's where ε =1/2) then transporting the clock very slowly such that a/c ≈ 0 then the clocks remain synchronized in that convention.
You cannot know time dilation without the assumption of a synchronization convention.
t'/t = f'/f = (1 - v/c) / γ = γ / (1 + v/c) = (1 - a/c) / (1 + b/c) γb/γa where v = (a + b) / (1 + a b /c²)
Time dilation could be : τ = t / γ or τ = γ t or τ = γb/γa t these are all different. Given a t, τ could be 0 to infinity even if v is arbitrarily small.
We CANNOT measure time dilation τ by any known means. What we can measure in a lab is observed time t' and our time t. We can only measure values locally. No matter what assumptions we make t' and t are symmetric.
Einstein assumes the form t'/t = (1 - v/c) / γ then he assumes c t = x AKA light moves at c in both directions.
t'/t = (1 - v/c) / γ → t' = (t - v/c t) / γ → t' = (t - v x/c²) / γ
I could assume the speed of light is c± = c / (1 ± κ) where κ = 0 to 1
For example c- = ∞ and c+ = 1/2c when κ = 1
Round trip speed would be:
t = 1/2 (x/c- + x/c+) = 1/2 (x/∞ + x/(1/2c)) = x/c as expected. David keeps saying 0 to 2c (c+ = c - |v| and c- = c + |v|) which wouldn't work relative to the clocks in that reference frame.
There is no need to invoke a preferred frame here because all physics we've ever done allows us to pick any κ and ε we choose. We could choose ε = 1/2 and κ = 0 (like Einstein) or any other possible value we wish (we could even have that same new value for all reference frames; this works in GR without modification). LET uses all values where each frame uses a different κ and ε. Using all values this has the ability to match SR mathematically (but would require modification to GR at yet untested extremes).
In any case like I've shown many times we can't measure the one-way speed of light independent of a synchronization convention. Unless experiments prove otherwise there is no error as David keeps implying because we are free to choose any convention we wish. He's pushing his idea based on a preferred frame that could be true but cannot be verified/pinned down. I'm pushing against the idea that we should be pinned down to a certain ε when we can't verify it without using an arbitrary convention (no matter how useful the convention is). There is nothing magical about it. There is also no separating "larger" synchronization "errors" because we can't cut the Lorentz Transformation into pieces and treat those pieces separately without first assuming a convention. David is not understanding why the clock difference depends on distance. It has nothing to do with "errors" or time dilation but rather the plane of simultaneity chosen. We know the input to the equation t and the output t'. How we choose to arrange the right side of the equation so it "makes sense" to us depends on convention.
t2 = t1 + ε (t3 - t1)
https://en.wikipedia.org/wiki/One-way_speed_of_light
The above link explains how much of this works. There's no need to have
Post by: Bored chemist on 27/07/2017 21:00:13
but it's only going to be close to zero if the system's at rest.Good.
You can stop there.
Because from my point of view, it is at rest.
"If you assume you are moving at 50% the speed of light in the direction you're sending your flash of light, "
From my perspective, I'm quite clearly not, so it would be an odd assumption.From my point of view, it's not an assumption, it's an observation.
As I said earlier, the Universe at large will certainly include things which are moving WRT me and their views on many things will differ from mine.
Post by: David Cooper on 27/07/2017 21:52:10
Unless experiments prove otherwise there is no error as David keeps implying because we are free to choose any convention we wish.
I have spoken of two errors, one of which is larger the faster you move one clock while not moving the other clock (which you assume to be at rest). That error is real and predictable, so it can be corrected for. Even if you move the clock extremely slowly, an error of that kind will remain - all you can do is decrease its size until it becomes small enough that you have less need to bother making a correction. In denying the existence of that error, you are only going to confuse people who can see that it must exist.
Quote
He's pushing his idea based on a preferred frame that could be true but cannot be verified/pinned down.
The whole business of trying to measure the one-way speed of light necessarily brings in the idea of an absolute frame if you imagine that light can travel relative to you at a speed other than c, so of course we have to explore this on that basis.
Quote
There is nothing magical about it.
If light is moving relative to you at c and you then accelerate towards the source of the light until you are moving at high speed towards it, the light can only still be moving relative to you at c if the universe runs on SR's magic. If we could determine the one-way speed of light and found it to be the same in both cases, then we would know that it does run on that kind of magic. The jury is still out on that though, because we can't determine the one-way speed of light to disprove SR directly.
Quote
David is not understanding why the clock difference depends on distance. It has nothing to do with "errors" or time dilation but rather the plane of simultaneity chosen.
One or other of us has certainly failed to understand this fully, and if it's me, I want to find that out.
If we assume that the middle of my three clocks is stationary and move the other two away from it very slowly so that the error (which you say doesn't exist) is minimised, we have three clocks ticking almost in sync. The outer two are certainly ticking in sync. What happens though if we decide that the middle clock is moving and we move the others so slowly that they're moving at almost the same speed while we relocate them? We now see these go past us because we are stationary, and we ought to see the front clock lag with its displayed time behind the other clocks while the rear clock moves ahead of the others with its time. We can get a God's eye view of this by taking photographs with a special kind of video camera where the clocks move directly past the pixels and practically touch them (no lens needed - this is like making a contact print) - each pixel records light when its own clock tells it to, and all the pixel clocks are synchronised for the frame of reference that we're using.
Now, here's the problem. If the clocks are moving so slowly that there is no error of the second type creeping in (due to different time dilations applying to different clocks while they're being moved apart), they must stay in sync in BOTH frames. They cannot possibly be ticking simultaneously in both frames though, so how can they get out of sync in the absolute frame where we watch the system moving past us?
Post by: David Cooper on 28/07/2017 16:23:28
Now, here's the problem. If the clocks are moving so slowly that there is no error of the second type creeping in (due to different time dilations applying to different clocks while they're being moved apart), they must stay in sync in BOTH frames. They cannot possibly be ticking simultaneously in both frames though, so how can they get out of sync in the absolute frame where we watch the system moving past us?
The reality is that time dilation has a crucial role. There are a couple of ways of controlling things as the two outer clocks are moved away from the middle one. One way is to move them a measured distance at a measured speed, but if the system is moving, one of those clocks will take longer to complete the trip than the other (because relative to the middle clock, one of the moving clocks will be moving slower than the other for relativistic reasons), which means the other clock will be back to ticking at the same speed as the middle clock sooner, changing its tick rate before the other moving clock changes its tick rate to match. The other obvious way of controlling things is to move each clock for a set amount of its measured time at a fixed speed, and once its time hits the target, you stop moving it - this has the same result with the time dilation difference causing one clock to hit the target sooner. Either way, the time dilation has a key role in how the events pan out. The idea that time dilation can be excluded from this by moving the clocks at infinitely slow speed is a misuse of mathematics and would lead to the clocks ticking in sync in both frames of reference once separated.
Post by: guest4091 on 29/07/2017 19:04:02
refer to graphic.
The left side represents the description of events by U, the rest frame by definition.
A moves parallel to U in the x direction at .6c. A chooses to synchronize two slave clocks to the master clock at x=0. One s-clock is located 1 unit distance ahead x=.8 (length contraction), and the other behind x=-.8 (not shown for clarity), Two light signals (blue) are emitted at t=0, to start both clocks (events R1 and R2), and get a reading returned to A (event D) at t=2g. Events R1 and R2 establish the axis of simultaneity for A, represented by line 0-Ax. The red line transforms U-time to A-time, thus At for D is 2.00. Next A sends a signal to set the clocks to the current time t plus half the transit time1. The s-clocks are synchronized to the m-clock.
The right side represents the description of events by A.
Notice
1. the SR synch convention provides the correct value for x according to what A perceives, assuming a pseudo rest frame.
2. the event R1 and convention assigned (R1) both occur at the same distance Ux=2, which is Ax=1.6. I.e. it doesn't make any difference since the round trip time is the same for both.
The practicality of 3 or more clocks allows 1 expensive precision clock to maintain the efficiency of a system of common clocks for the masses. It's what is done every day in our world.
https://app.box.com/s/umw5stjtqwoo7pqjv2h322psnwngetnb
Post by: guest4091 on 29/07/2017 19:14:15
The lost time is
x/a[√(1-aa)-1]
(4) I can set the cameras to record the clock in the foreground and the flash in the background
(6) I can look record at the time on the clock when the flash arrives.
(7) I can calculate the speed as distance divide by the time difference.
The light must return for you to be aware of a distant event.
If you are assuming a pseudo rest frame, you accept the path lengths are equal.
If you assume being in motion, and the path lengths are different, the synched clocks return the same reading, despite the fact the path sequence is reversed.
The fundamental problem is, you are present at the local events, emission and detection. You are not present at the distant reflection event. You can know where it occurred but not when.
Of course there are limits to what's practical vs ideal!
Post by: Bored chemist on 29/07/2017 22:07:56
The light must return for you to be aware of a distant event....Not really. I go to the camera later and look at the film. The camera was (sort of) "aware" of the event, and it recorded it as well as recording the local time of that event.
The fundamental problem is, you are present at the local events, emission and detection. You are not present at the distant reflection event.
...
There is no "reflection event".
Post by: guest39538 on 30/07/2017 19:36:29
If r1=r2 and light travels both vectors simultaneously, both the detection points detect the light in the same time.
He said no , he is quite mad I think.
Post by: guest4091 on 31/07/2017 18:01:17
The red hyperbola, referred to as the calibration curve by Max Born, in his book on Relativity, is a line of constant time where it intercepts the time lines of objects moving at varying speeds. I.e. the faster it moves, the longer it takes to indicate t on a moving clock. The pair is set to the m clock. In test 1 the pair separates from m at a fast speed, with a large difference in time dilation, as shown by the green line c1-c1. The slope is greater than s1-s2.
In test 2 the pair separates from m at a slower speed, with a small difference in time dilation, but a total time of 2t (not shown to avoid clutter, and v=half of first speed ), as shown by the green line c2-c2. The slope is much closer to s1-s2.
The slope of s1-s2 is actually tangent to the calibration curve at m.
Conclusion:
Slow clock transport more closely approximates the SR convention as the separation speed v decreases. The statement "it equals the SR convention at v=0" would be redundant, since it is equivalent to "if you don't move them, they will stay synchronized".
I think Dutch was referring to this aspect of synchronization.
https://app.box.com/s/59yk88qpfjodkwxsk3faii8eqwjyydwz
Post by: guest4091 on 31/07/2017 18:13:09
Not really. I go to the camera later and look at the film. The camera was (sort of) "aware" of the event, and it recorded it as well as recording the local time of that event.Assuming you think you are moving:
There is no "reflection event".
For the camera to record the background event requires a 2-way trip.
How do you know the difference in the clock there and your local clock?
Post by: Bored chemist on 31/07/2017 19:25:39
Did you actually read what I posted about the scenario I'm talking about?Not really. I go to the camera later and look at the film. The camera was (sort of) "aware" of the event, and it recorded it as well as recording the local time of that event.Assuming you think you are moving:
There is no "reflection event".
For the camera to record the background event requires a 2-way trip.
How do you know the difference in the clock there and your local clock?
It's the one where I'm at rest (at least in my frame of reference) and where there are two synchronised cameras which record a singe event from different distances.
Post by: guest4091 on 01/08/2017 20:31:20
Did you actually read what I posted about the scenario I'm talking about?Look at the right side of the graphic in #78. If someone in the theoretical 'fixed frame' U was observing your moving frame, with a flash from you to a distant object, on a long leg out and returning on a short leg, using SR conventon, you in your pseudo rest frame assigns equal legs, with the same round trip time. The answer will be the usual, light speed is c. You can check the Lorentz/SR coordinate transformations to verify that x'/t' = x/t = c, where the primed coordinates are your measurements. That is the very reason you can assume a pseudo rest frame. Pseudo because there is no real rest frame (that can be used as a common reference for measurements). It's not a conspiracy, it's because light propagation is constant and independent of source.
It's the one where I'm at rest (at least in my frame of reference) and where there are two synchronised cameras which record a singe event from different distances.
Post by: guest39538 on 01/08/2017 20:35:08
There is a rest frame, the observed darkness background of space, space itself is not observed to move. Relative to bodies , space is at rest and all bodies are moving relative to space.Did you actually read what I posted about the scenario I'm talking about?Look at the right side of the graphic in #78. If someone in the theoretical 'fixed frame' U was observing your moving frame, with a flash from you to a distant object, on a long leg out and returning on a short leg, using SR conventon, you in your pseudo rest frame assigns equal legs, with the same round trip time. The answer will be the usual, light speed is c. You can check the Lorentz/SR coordinate transformations to verify that x'/t' = x/t = c, where the primed coordinates are your measurements. That is the very reason you can assume a pseudo rest frame. Pseudo because there is no real rest frame (that can be used as a common reference for measurements). It's not a conspiracy, it's because light propagation is constant and independent of source.
It's the one where I'm at rest (at least in my frame of reference) and where there are two synchronised cameras which record a singe event from different distances.
All things move relative to the rest frame of space observably.
Post by: Bored chemist on 01/08/2017 21:36:48
If I look at it, the first thing I see is that it's rather unclear- just a bunch of lines and letters.
Look at the right side of the graphic in #78.
The second thing I see is that it's not a representation of the scenario I put forward.
Why is everyone so reluctant to answer the simple question I asked?
If I get 2 clocks, sync them, separate them slowly enough that the time dilation is small and put them in front of 2 video cameras.
I the set off a flash- nearer to one camera than the other.
I look at the video and I note when the flash arrives at each camera.
I know the difference in paths and I know the difference in times.
So, what will I get if I divide the distance by the time?
Post by: guest39538 on 01/08/2017 22:04:52
speed? It is the same way I did it with the graph using one detector.If I look at it, the first thing I see is that it's rather unclear- just a bunch of lines and letters.
Look at the right side of the graphic in #78.
The second thing I see is that it's not a representation of the scenario I put forward.
Why is everyone so reluctant to answer the simple question I asked?
If I get 2 clocks, sync them, separate them slowly enough that the time dilation is small and put them in front of 2 video cameras.
I the set off a flash- nearer to one camera than the other.
I look at the video and I note when the flash arrives at each camera.
I know the difference in paths and I know the difference in times.
So, what will I get if I divide the distance by the time?
Post by: guest4091 on 02/08/2017 16:58:56
BC;
I've read your posts from #70 on, trying to get a picture of your setup. Your last post helped.
Is this correct?
You are at x=0 with a camera and clock1.
A 2nd camera and clock2 are at say x=10.
The flash occurs at x=6.
Both cameras record the flash and the local time.
You expect the clocks are synched to within an insignificant amount by slow transport.
If it is correct, then (6-4)/(6-4) = 1. (light speed)
Post by: David Cooper on 02/08/2017 18:51:07
So, what will I get if I divide the distance by the time?
You'll get the apparent speed of light for a round trip. Your synchronisation method tunes your apparatus to its speed of movement through space such that your measurement hides that movement.
Post by: Bored chemist on 02/08/2017 20:29:11
A trip "round" what?So, what will I get if I divide the distance by the time?
You'll get the apparent speed of light for a round trip. Your synchronisation method tunes your apparatus to its speed of movement through space such that your measurement hides that movement.
Incidentally, from my perspective the apparatus isn't moving through space: no tuning needed.
Post by: David Cooper on 02/08/2017 21:55:13
A trip "round" what?
A round-trip is a 2-way trip.
Quote
Incidentally, from my perspective the apparatus isn't moving through space: no tuning needed.
That's the whole issue - you're assuming you're stationary up front, you're synchronising your clocks to fit with your idea that you're stationary, and then you're measuring the "one-way" speed of light on that false basis. You cannot move your clock infinitely slowly because infinite slowness won't move it at all, so you have to move it as some speed greater than zero, and while you are moving it there are time dilation effects which tune your clock synchronisation in such a way as to maintain the illusion that your system is stationary. Your measurement of the distance travelled by the moving and "stationary" clocks is an unknown because you can't tell how far they're really moving while you move one of your clocks away from the other. If the system is moving at very high speed, both clocks may have moved a lightyear and the time dilation difference between the "moved" and "unmoved" clocks will be more severe.
Post by: Bored chemist on 02/08/2017 22:29:42
A round trip implies that you go somewhere and then come back.A trip "round" what?
A round-trip is a 2-way trip.QuoteIncidentally, from my perspective the apparatus isn't moving through space: no tuning needed.
That's the whole issue - you're assuming you're stationary up front, you're synchronising your clocks to fit with your idea that you're stationary, and then you're measuring the "one-way" speed of light on that false basis. You cannot move your clock infinitely slowly because infinite slowness won't move it at all, so you have to move it as some speed greater than zero, and while you are moving it there are time dilation effects which tune your clock synchronisation in such a way as to maintain the illusion that your system is stationary. Your measurement of the distance travelled by the moving and "stationary" clocks is an unknown because you can't tell how far they're really moving while you move one of your clocks away from the other. If the system is moving at very high speed, both clocks may have moved a lightyear and the time dilation difference between the "moved" and "unmoved" clocks will be more severe.
At what stage in the process I described does anything come back?
I look at the "near" camera and see when the flash arrived, then I go and look at the "far" camera and see when the flash arrived. Then I do the arithmetic.
The only thing that "comes back" in any way is me and as I keep pointing out, I can make the relativistic effects there as small as I like.
"because you can't tell how far they're really moving while you move one of your clocks away from the other"
I forgot to mention- there's a railway track along the route I chose to move the clock.
I can count railway sleepers.
I can also check that each sleeper is the same distance as the last one- because I have a ruler.
As long as I go slowly, the length of the ruler is as near constant as I like.
"you're assuming you're stationary up front"
And, once again, from my point of view, it's not an assumption, it's an observation.
For the sake of discussion, let's assume I start by destroying the rest of the universe.
Post by: guest4091 on 03/08/2017 17:03:42
I wasn't making your example difficult. If you provide distances for all the objects involved as measured from a common location it's easier to visualize. General terms like foreground, near, etc. are vague.
Your example is just a single 1-way trip divided into 2 parts, i.e. set the origin at the location of the flash.
Let's put your example in a realistic perspective. One light second is just short of 1.25 ls, the time for light to travel between the surface of the earth to the surface of the moon. Thus your clock should measure ns (nano seconds), and the distance unit 1 foot or .3 m.
Set clock 2 (c2) and a camera at 3 m distance, send a flash across that distance to c2.
Assuming your clocks are synched to less than 1 ns, c2 reads 3 ns.
If you had sent a flash at t=0, that reflected from a mirror at c2, it would return at t=6.
The SR synch convention would have set c2 to indicate 1/2 of the round trip,6/2=3.
Just as in the MMX, regardless of speed, the observer perceives the td time and lc distance, as if he is not moving, i.e. x/t=c.
Post by: Bored chemist on 03/08/2017 19:37:30
I've read your posts from #70 on, trying to get a picture of your setup.
If you provide distances for all the objects involved as measured from a common location it's easier to visualize.
Only if you read the distances I provided; you didn't.
Feel free to try reading from the start and see if that helps.
Post by: David Cooper on 04/08/2017 01:56:08
A round trip implies that you go somewhere and then come back.
At what stage in the process I described does anything come back?
Your clocks function by counting round-trip cycles of something moving, and while you move one of your clocks, those round-trips are affected by that movement regardless of how slowly you move it.
Quote
and as I keep pointing out, I can make the relativistic effects there as small as I like.
No you can't. All you can do is minimise the big error while making no difference to the residual error, but the only way you're going to see how these errors come into play is by producing a table of data to show it all clearly, so I'm going to help you build such a table.
Quote
I can also check that each sleeper is the same distance as the last one- because I have a ruler.
As long as I go slowly, the length of the ruler is as near constant as I like.
You can't tell how much length-contraction might be acting on the track, and you don't know how far you've moved your moving clock through space either (or how far you've moved your "stationary" clock).
Quote
"you're assuming you're stationary up front"
And, once again, from my point of view, it's not an assumption, it's an observation.
If you're doing this on one planet and your cousin is doing the same thing on another planet moving relative to yours, both of you are making the same claim to be stationary, and at least one of you is being fooled.
Quote
For the sake of discussion, let's assume I start by destroying the rest of the universe.
That's not going to help you do anything other than help you deceive yourself. Let's just build the table and do the maths. We want to generate numbers for two cases, one where we assume the system is stationary and the other where we assume it's moving at very high speed. We then want to generate numbers for each case using a range of numbers for moving the clock at different speeds, so I'll show you a method for doing the calculations which you can apply yourself to extend the table if you want to use slower speeds than the ones I've chosen for relocating your clock.
Let's start with case 1, where we assume the system is stationary. If we move the clock at the speed of light (1c) and move it a distance of one lightsecond, it will not tick at all while it's being moved, so it will end up ticking one whole second behind the stationary clock. If we move the clock at 50% the speed of light instead (0.5c), we can work out how much the clock will be slowed by finding the inverse sine of 0.5 and then finding the cosine of that answer. That comes out as 0.866 ticks per second, meaning that the moved clock has lost 0.134 of a second while it was being relocated. Because we're assuming that the system is stationary, we can always calculate how to correct the moved clock to make up for the time it has lost, so we can ensure that our clocks are perfectly synchronised for the frame of reference in which the system is stationary regardless of how fast we move the clock. Let's now try 10% the speed of light (0.1c): cos(arcsin(0.1)) = 0.995, so the clock has lost 0.005 of a second. So, here's the first column of our table (speed; relative tick rate for moving clock compared with stationary clock; lost time for moved clock compared with stationary clock; correction value; corrected value):-
1c, 0, 1, 1, 0
0.5c, 0.866, 2 x 0.134, 2 x 0.134, 0
0.1c, 0.995, 10 x 0.005, 10 x 0.005, 0
You can extend that as much as you like, but remember that we can remove the big error in each case simply by working out how much time the clock must have lost and adding it back on. As we use slower and slower clock transport, the uncorrected results tend towards the corrected results (which are all zero), but they never quite get there, so you should always make the adjustment if you want to maximise the accuracy.
Now we need to start to build our second column, but it takes a bit more work. We need to choose a speed for the system to move through space at (the system being the "stationary" clock and anything that remains at rest relative to it), and you can add more columns of your own to cover any speed you fancy if you don't like my choice. I'm going with 0.866c. At this speed, our 1 lightsecond distance has been length-contracted to 0.5 of a lightsecond. (You can calculate the length-contraction for any other speed you want to work with in the same way as you calculate the time dilation.) The relative speeds of travel are also affected by the speed of travel of the system because of relativistic mass complications, so we have to do some extra calculations to convert to their real speeds of travel through space. For example, we naively think that light moves at 1c faster than the system if we're at rest with the system, but because the system is actually moving at 0.866c, for light to be moving at 1c relative to the system it would have to be moving through space at 1.866c which is clearly impossible. We know that light always travels through space at c though, so it must be moving relative to the system at 0.134c.
We have to correct our other speeds too, because with our 0.5c speed for moving a clock relative to our "stationary" clock which is moving at 0.866 we can't just add the two speeds together as again it would mean moving a clock through space faster than the speed of light. The formula for adding velocities correctly involves adding the two together (as you might expect), but then dividing the answer by 1 + the two velocities multiplied by each other, so that's (0.866 + 0.5) / (1 + 0.866 x 0.5). The answer is 0.953c. The time dilation for that speed is 0.3022. We now need to work out how long it will take for the clock to move to it's destination, and that's going to involve a longer distance travelled than the 0.5 lightsecond length of the course because the system (including the course) is moving along at 0.866c. So, we need to know how long it will take for an object moving at 0.953c to close in a distance of 0.5 lightsecond on something that's moving away from it at 0.866c. (Note: I stored all the values in memories on a calculator with 9 memories so as to be able to reuse them more easily on subsequent steps without losing any accuracy, and I also used sin 60 to get a more precise value than 0.866 which is just a close approximation of the speed which dilates time and contracts lengths by exactly 0.5x, so every time I write 0.866c I expect you to type in and use sin 60 instead.) The closing speed is 0.953 - 0.866 = 0.0872, so we can divide the 0.5 lightsecond figure by this to get the time taken for the clock to move to its destination, and that gives us the time 5.732s. (The distance the clock actually moves through space during its relocation is therefore 0.953 x 5.733 = 5.46 lightseconds, but we don't need to use that figure in building our table.) We know that the clock is moving at 0.953c for 5.733 seconds with a time dilation of 0.3022 applied to it, so during that 5.733 seconds it is only measuring 5.733 x 0.3022 seconds as having passed for it while our stationary clock is measuring 5.733 x 0.5 seconds as having gone by. The difference between these two numbers is the actual amount of time lost by the moved clock, and that value is 1.1339.
Let's now do the same for 0.1c: (0.866 + 0.1) / (1 + 0.866 x 0.1) = 0.889c. The time dilation for that speed is 0.4578. We need to know how long it will take for an object moving at 0.889c to close in a distance of 0.5 lightsecond on something that's moving away from it at 0.866c. The closing speed is 0.889 - 0.866 = 0.023, so we divide the 0.5 lightsecond figure by this to get the time taken for the clock to move to its destination, and that gives us the time 21.732s. We know that the clock is moving at 0.889c for 21.732s with a time dilation of 0.4578 applied to it, so during the 21.732s it is only measuring 21.732 x 0.4578 seconds as having passed for it while our stationary clock is measuring 21.732 x 0.5 seconds as having gone by. The difference between these two numbers is the actual amount of time lost by the moved clock, and that value is 0.91615.
You can repeat that process for any other speeds you like, but to complete my part of the table we still need to work out what happens if the clock is moved at the speed of light, so I'll do that bit now. The closing speed this time is 1c - 0.866 = 0.134, so we divide the distance 0.5 by this to get the time taken for the clock to get into position, and that comes to 3.73s. During this time, the stationary clock gains time over the moving clock, but as it's ticking at 0.5 the rate of the time of the stationary reference frame, that means the moved clock loses 1.866s
(Note that the values that we correct the end result by are the same as in the previous table because they will still be calculated by the naive experimenters on the basis that the system is not moving, so these are the corrections they will make - we are describing the exact same events so we can't change the history as to which correction values they apply.) So, here's the new column for the table (speed, relative tick rate for moving clock compared with "stationary" clock; lost time for moved clock compared with "stationary" clock, correction value, corrected value):-
1c, 0, 1.866s, 1, 0.866s
0.5c, 0.6044, 1.1339s, 2 x 0.134, 0.8659s
0.1c, 0.9157, 0.91615s, 10 x 0.005, 0.866s
So, what have we learned from this? Look at the corrected times on the right. They are all the same (or would be if we used more accurate correction values rather than the approximations 0.134 and 0.005). That is how much the moved clock's time lags behind the "stationary" clock, and it's the same lag regardless of the speed at which the clock is moved. You can copy the way I did the calculations for moving the clock slower and slower, but if the system's moving at 0.866c, the residual error will always be 0.866.
What happens then if you measure your "one-way" speed of light? In case 1 your clocks are correctly synchronised because the system is stationary, and because your clocks are ticking in sync, it will take one second for light to move one lightsecond. In case 2, your clocks are out of sync. Light leaves one clock and has to chase after another clock which is 0.5 of a lightsecond ahead of it and which is moving away from it at 0.866c, so its closing speed is 0.134c. We divide 0.5 by this and get 3.73s. During this time, our clocks are ticking half as slowly, so they advance by 1.866 seconds, and that gives the experimenters a timing for the light of 1 second to cover the distance which they mistakenly think is 1 lightsecond long while they also mistakenly think their clocks are ticking in sync.
Post by: dutch on 04/08/2017 18:46:45
I have spoken of two errors, one of which is larger the faster you move one clock while not moving the other clock (which you assume to be at rest). That error is real and predictable, so it can be corrected for.
There is no "error." Even from a LET framework all reference frames still work just fine even if ε=1/2 only for one of them. Furthermore, LET doesn't give you the option to know a true rest frame so you can't "correct" for the “error.” You first must do one thing... CHOSE A CONVENTION. Everything else you show is a result of this choice including time dilation. Unless you're God or you know how to break Lorentz Invariance, there is no error just choice of convention. It's a convention because we just arbitrarily agree to it and THEREFORE arbitrarily agree to the one-way speed of light. Time dilation has no objective reality we can test unless there are round trips (like the Twins Paradox). The one-way speed of light is set BEFORE we even consider time dilation by choice of convention. Time dilation only shows how we can’t distinguish between our infinite choices.
The whole business of trying to measure the one-way speed of light necessarily brings in the idea of an absolute frame if you imagine that light can travel relative to you at a speed other than c, so of course we have to explore this on that basis.
No, Einstein just chose ε =1/2. He chose it because it made the math easier, but he could have chosen ε =1/4, ε =1000, or ε =1/1000. You could have a convention where you always choose ε = 1/4 for your point of view. You could even make a block universe where ε =1/4 for your own viewpoint. What LET suggests is a unique true ε (from a "God's" view) exists for every single velocity (forcing a system to exist for how ε changes with velocity and gravity). This may be true but it adds considerable more complexity when applying it to General Relativity and doesn't work with the extremes of GR (perhaps GR is broken at the extremes). GR is already complex and this increases the complexity by a significant factor.
That ε can be arbitrarily chosen is good enough. I don't need to have the extra assumption that ε is different in an absolute sense for every frame. SR believers simply do not believe this at all. I know you like LET which is fine but you're opening an entire can of worms that is unnecessary to prove that we can't measure the one-way speed of light WITHOUT referring to an arbitrary convention.
Now you can personally think that one convention is "true" but you cannot prove it.
Now I personally think it's weird that people automatically assume ε=1/2 for them no matter what (often in an absolute sense) forcing them to look at other frames with ε ≠ 1/2 at least from their chosen perspective. However, I can't stop them from doing this because it mathematically works. Shoving LET down their throats doesn't work. I can point out that ε =1/4 etc would also work and that ε=1/2 is arbitrarily chosen in SR.
If we assume that the
You mean if you assume a convention? Stop, that's all you need to say to prove the one-way speed of light is unknown without a convention.
Now, here's the problem. If the clocks are moving so slowly that there is no error of the second type creeping in (due to different time dilations applying to different clocks while they're being moved apart), they must stay in sync in BOTH frames. They cannot possibly be ticking simultaneously in both frames though, so how can they get out of sync in the absolute frame where we watch the system moving past us?
You're invoking an absolute frame again when all anyone must do is show that ε is arbitrarily chosen. I don't care if you use LET or SR both set ε arbitrarily. Both assume a framework we can't verify. One by forming a block universe where ε=1/2 everywhere locally and the other via an absolute rest frame where ε=1/2 absolutely for only one frame. The underlying reason behind our ability to choose is we have no way to tell what ε equals because whatever we choose it doesn't alter experiments.
We CHOOSE a plane of simultaneity. Sure, clocks moving in other reference frames time dilate moving in one direction but ONLY after we assume our choice of convention.
t'/t = f'/f = (1 - v/c) / γ = γ / (1 + v/c) = (1 - a/c) / (1 + b/c) γb/γa where v = (a + b) / (1 + a b /c²)
Time dilation could be : τ = t / γ or τ = γ t or τ = γb/γa t these are all different. Given a t, τ could be 0 to infinity.
LET says we can't locate the absolute rest frame so it also chooses a convention based exactly on the math above. SR does the same thing based on the math above.
Quote
I have spoken of two errors, one of which is larger the faster you move one clock while not moving the other clock (which you assume to be at rest). That error is real and predictable, so it can be corrected for. Even if you move the clock extremely slowly, an error of that kind will remain - all you can do is decrease its size until it becomes small enough that you have less need to bother making a correction. In denying the existence of that error, you are only going to confuse people who can see that it must exist.
Why do you keep bringing in "errors of the second type?" If an absolute rest frame exists such that ε=1/2 only absolutely relative to that reference frame, then clocks moving at v still work normally. They may run slower but that's not an "error" as the clocks are working as they should. There aren't two sources of errors there's time dilation and that's it. As an object moves at v with a specific time dilation then the clocks would get out of sync. How much they get out of sync one-way depends on distance at a specific v AFTER we choose the "rest frame."
t' = (t - v x/c²) / γ Let t = 0 then we have t' = v x/c² / γ → t' is proportional to x as v → c γ → 0
The above isn't a "second error." Time dilation gets clocks out of sync regardless. You're assuming a "first error" relative to an arbitrarily set absolute rest frame (at least from our point of view) and a second error relative to another arbitrary frame moving at velocity v. Both “errors” are relative to whatever frame of reference/convention we choose. You can account for this “error” exactly but ONLY after assuming a convention. You can make the “error” arbitrarily small (slow clock transport) but ONLY with respect to a chosen convention. Other conventions would have the “error” significantly larger (in terms of the speed of light it could be infinitely off with another convention; simultaneity on the other hand is bounded by the two-way speed of light).
The one-way speed of light is literally chosen by convention in our mathematics. If it does have a definite value for a specific reference frame like both SR AND LET claim then we simply have no way to measure it.
Post by: David Cooper on 04/08/2017 21:52:33
I have spoken of two errors, one of which is larger the faster you move one clock while not moving the other clock (which you assume to be at rest). That error is real and predictable, so it can be corrected for.
There is no "error."
If a clock runs slow because it's moved, it fails to record all the time that has passed for it, and that results in an error in its timing. The faster you move it, the bigger that error is.
Quote
Even from a LET framework all reference frames still work just fine even if ε=1/2 only for one of them. Furthermore, LET doesn't give you the option to know a true rest frame so you can't "correct" for the “error.”
I don't know if you understand how reasoning works, but it's generally conditional using IF and THEN clauses. E.g. IF the system is stationary, THEN a clock moving through the system runs slow. While we are discussing things under that condition ("IF the system is stationary"), everything said is governed by that condition. When we switch to a different condition such as "IF the system is moving at 8.866c", everything we then say is governed by that new condition. The fact that we can't tell which of the cases is true does not negate the truth (conditional truth) of what is said about that case on the basis that it's true if the condition is true and may not be true if the condition is false.
Quote
You first must do one thing... CHOSE A CONVENTION.
No, you choose a frame of reference. Choosing a convention then gives you the same result no matter which valid convention you go for.
Quote
Everything else you show is a result of this choice including time dilation.
Everything I show is a result of which frame you choose to use.
Quote
Unless you're God or you know how to break Lorentz Invariance, there is no error just choice of convention.
You are choosing a frame, and you are almost always choosing the wrong one. Your results will seem just as valid as any others because you can't tell who's right, but the underlying mechanism must be a rational one and must hold a truth about what is happening which it doesn't reveal to us. That doesn't stop us looking at the way the mechanism works though by working through things on a conditional basis.
Quote
The one-way speed of light is set BEFORE we even consider time dilation by choice of convention.
It's the choice of frame that selects a proposed one-way speed of light relative to the system.
Quote
The whole business of trying to measure the one-way speed of light necessarily brings in the idea of an absolute frame if you imagine that light can travel relative to you at a speed other than c, so of course we have to explore this on that basis.
No, Einstein just chose ε =1/2. He chose it because it made the math easier, but he could have chosen ε =1/4, ε =1000, or ε =1/1000. You could have a convention where you always choose ε = 1/4 for your point of view. You could even make a block universe where ε =1/4 for your own viewpoint.
You choose a frame of reference and thereby conditionally assert that the speed of light is the same relative to that frame in all directions. That makes the speed of light not equal to c relative to objects moving through that frame in most directions and provides a different theory as to the reality of the situation to any of the theories based on using different frames (all of those theories being in contradiction of each other as only one of them can be true).
Quote
That ε can be arbitrarily chosen is good enough. I don't need to have the extra assumption that ε is different in an absolute sense for every frame. SR believers simply do not believe this at all. I know you like LET which is fine but you're opening an entire can of worms that is unnecessary to prove that we can't measure the one-way speed of light WITHOUT referring to an arbitrary convention.
Your choosing a convention is simply selecting a frame to act as an absolute frame and thereby setting yourself up to measure the speed of light relative to that frame as c.
Quote
Now you can personally think that one convention is "true" but you cannot prove it.
There can only be one truth for the universe regardless of whether we can identify it or not.
Quote
Now I personally think it's weird that people automatically assume ε=1/2 for them no matter what (often in an absolute sense) forcing them to look at other frames with ε ≠ 1/2 at least from their chosen perspective. However, I can't stop them from doing this because it mathematically works. Shoving LET down their throats doesn't work. I can point out that ε =1/4 etc would also work and that ε=1/2 is arbitrarily chosen in SR.
If you restrict yourself to ε=1/2, you are selecting the frame of reference in which the system is at rest, and that sheds no light on anything. It's only when you work things through using at least two different reference frames that you can gain a real understanding of what's going on.
Quote
If we assume that the
You mean if you assume a convention? Stop, that's all you need to say to prove the one-way speed of light is unknown without a convention.
It's much easier to understand that you're choosing a particular frame of reference, and that's all your convention actually is, so why are you objecting to me calling a spade a spade instead of burying it in obfuscation?
Quote
Now, here's the problem. If the clocks are moving so slowly that there is no error of the second type creeping in (due to different time dilations applying to different clocks while they're being moved apart), they must stay in sync in BOTH frames. They cannot possibly be ticking simultaneously in both frames though, so how can they get out of sync in the absolute frame where we watch the system moving past us?
You're invoking an absolute frame again when all anyone must do is show that ε is arbitrarily chosen. I don't care if you use LET or SR both set ε arbitrarily. Both assume a framework we can't verify. One by forming a block universe where ε=1/2 everywhere locally and the other via an absolute rest frame where ε=1/2 absolutely for only one frame. The underlying reason behind our ability to choose is we have no way to tell what ε equals because whatever we choose it doesn't alter experiments.
What I've done is point out that infinitely slow transport (which can't be done because infinitely slow will never separate the clocks at all, but if it could by magic be done...) would lead to the separated clocks remaining in sync in all frames (which is impossible) rather than just one, but you don't seem to have taken that on board.
Quote
We CHOOSE a plane of simultaneity.
Yes - a frame of reference.
Quote
Sure, clocks moving in other reference frames time dilate moving in one direction but ONLY after we assume our choice of convention.
All frames of reference apply to every scenario, so most of them need time dilation to act on your "infinitely slowly moving" clocks, which means they can't be moving infinitely slowly relative to the "stationary" clock (or relative to another "infinitely slowly moving" clock "moving" in the opposite direction) if the time dilation differences are able to act. The idea of moving them infinitely slowly and having no time dilation act on them at all requires the synchronisation to remain in place for all frames, and that's impossible - that's why you should be banned from using it as an any kind of explanation of what's going on.
Quote
t'/t = f'/f = (1 - v/c) / γ = γ / (1 + v/c) = (1 - a/c) / (1 + b/c) γb/γa where v = (a + b) / (1 + a b /c²)
Time dilation could be : τ = t / γ or τ = γ t or τ = γb/γa t these are all different. Given a t, τ could be 0 to infinity.
LET says we can't locate the absolute rest frame so it also chooses a convention based exactly on the math above. SR does the same thing based on the math above.
It's nothing more than choosing a frame of reference.
Quote
QuoteI have spoken of two errors, one of which is larger the faster you move one clock while not moving the other clock (which you assume to be at rest). That error is real and predictable, so it can be corrected for. Even if you move the clock extremely slowly, an error of that kind will remain - all you can do is decrease its size until it becomes small enough that you have less need to bother making a correction. In denying the existence of that error, you are only going to confuse people who can see that it must exist.
Why do you keep bringing in "errors of the second type?"
What? In that bit you've quoted which is all about the first type? The second type of error is the unidentifiable one that's left over once you think you've corrected for the first type.
Quote
If an absolute rest frame exists such that ε=1/2 only absolutely relative to that reference frame, then clocks moving at v still work normally. They may run slower but that's not an "error" as the clocks are working as they should.
If they are attempting to measure time, they are failing to record all of the time that has passed for them, so they are building up an error. They are counting cycles and they are correctly counting the number of cycles that have run through, so in that sense they are not producing an error. It therefore depends on what you expect of them as to whether you call it an error or not, and I call it an error on the basis that they are failing to measure all the time that's passed for them. That is a perfectly sound basis to work upon.
Quote
There aren't two sources of errors there's time dilation and that's it. As an object moves at v with a specific time dilation then the clocks would get out of sync. How much they get out of sync one-way depends on distance at a specific v AFTER we choose the "rest frame."
What I have done in dividing things up into two errors is fully sound. The first type of error is the component which you attempt to correct for on the basis that the system is not moving, and I separated it away from the total error in order to show how all the different speeds of travel for moving the "moving" clock can easily be corrected for to provide the same synchronisation as each other. If you move the clock fast, you make a big correction, and if you move it very slowly you make a tiny correction, but the result is the same. The point of doing this was to show that all speeds of movement for the clock are equivalent to just sending a signal at the speed of light to synchronise two clocks that are already separated and making a correction to that in the same way.
Quote
t' = (t - v x/c²) / γ Let t = 0 then we have t' = v x/c² / γ → t' is proportional to x as v → c γ → 0
The above isn't a "second error." Time dilation gets clocks out of sync regardless. You're assuming a "first error" relative to an arbitrarily set absolute rest frame (at least from our point of view) and a second error relative to another arbitrary frame moving at velocity v. Both “errors” are relative to whatever frame of reference/convention we choose.
My two errors can be regarded as a two parts of a single error if you like, in which case we can rename the first kind of error as one component of the error (the part we can attempt to correct on the basis that the system isn't moving) and another component of the error which would only be corrected for if we then adjust to the absolute frame. There can be situations where the attempt at correcting the first component actually takes it away from the correct value to a wrong one. But the whole point of dividing the error into these two categories is to correct for the first one to produce the same end value regardless of which speed was used to move the moving clock away from the stationary clock and have the same degree of synchronisation for the infinitely slow clock transport as for sending a signal at c. It's all about showing the equivalence of these methods so that it becomes clear that no matter how slowly you move your clock, you might as well just send a light signal to set up the clock timings and then use those clocks to time another flash of light over the same course.
Quote
You can account for this “error” exactly but ONLY after assuming a convention.
Which is an obfuscated way of saying that you can account for it exactly only after choosing a specific frame of reference to work with.
Quote
You can make the “error” arbitrarily small (slow clock transport) but ONLY with respect to a chosen convention. Other conventions would have the “error” significantly larger (in terms of the speed of light it could be infinitely off with another convention; simultaneity on the other hand is bounded by the two-way speed of light).
Which is an obfuscated way of saying, using other frames of reference as your base would lead you to use different correction values. All you're really doing here is objecting to my clear use of language and trying to impose your obfuscated language on me instead, but you're not going to get your way. I prefer to call a spade a spade because it leads to greater understanding. And once the first component of the error has been corrected for (usually on the basis that the system is stationary), there remains an error which is unidentifiable to us depending on which frame is the actual frame in which the speed of light is c relative to it in all directions.
Quote
The one-way speed of light is literally chosen by convention in our mathematics.
= The one-way speed of light is assumed to be c relative to the frame of reference chosen for the calculations.
Quote
If it does have a definite value for a specific reference frame like both SR AND LET claim then we simply have no way to measure it.
And I have made no claim that it can be measured by anything (other than the universe itself).
Post by: Bored chemist on 05/08/2017 12:12:02
If you're doing this on one planet and your cousin is doing the same thing on another planet moving relative to yours, both of you are making the same claim to be stationary, and at least one of you is being fooNo, I'm stationary from my PoV and he's stationary from his.
led.
But, since these viewpoints are different there's no contradiction.
Nobody is being "fooled"
As I have pointed out before, I know that other people who are moving WRT me will see things differently- so it's no surprise that they will interpret the experiment I'm doing differently and will think the one-way speed of light I measure is different.
I know that.
But, as I pointed out before, they won't even agree with me about the speed of the bus into town, so I don't expect them to agree with me about the one way speed of light.
I'm only interested in measuring it in my frame of reference.
ymmv
Post by: David Cooper on 05/08/2017 18:43:24
If you're doing this on one planet and your cousin is doing the same thing on another planet moving relative to yours, both of you are making the same claim to be stationary, and at least one of you is being fooled.
No, I'm stationary from my PoV and he's stationary from his.
But, since these viewpoints are different there's no contradiction.
Nobody is being "fooled"
Of course someone is being fooled. Let's put your two experiments closer together so they're sharing the same space. We can call your clocks A and B and your cousin's clocks A' and B'. You've both separated them and are ready to time light moving from A to B (or A' to B'). Clock B' passes clock A before you send the light signal out that you want to time. Indeed, clock A' is right alongside clock A when the two signals are sent. Your signal reaches clock B a second later (if you're the one who's stationary). His signal has not reached clock B' yet and has to go a long way further before it can. So if he thinks his light signal took one second to go from A' to B', he's wrong. If he's right, then he must be stationary and you must be the one that's moving.
Quote
As I have pointed out before, I know that other people who are moving WRT me will see things differently- so it's no surprise that they will interpret the experiment I'm doing differently and will think the one-way speed of light I measure is different.
I know that.
But, as I pointed out before, they won't even agree with me about the speed of the bus into town, so I don't expect them to agree with me about the one way speed of light.
I'm only interested in measuring it in my frame of reference.
In which case, you must be aware that you almost certainly aren't measuring the real speed of light relative to you.
I was wrong about all these methods measuring light on a round trip though - you're certainly getting the same result as if you were measuring it on a round trip, but it might not quite be that. If you were to move your clock at the speed of light, for example, that would be the same as sending light from position A to B to synchronise the clocks and then sending light from A to B to see how long it takes to cover that course as judged by those clocks, which is practically the same thing as using a light signal to time itself over the course, so there is nothing two-way about it. If you move the clock at speeds a bit less than c, it's slightly different because some cycling is taking place in the clock (each tick involving something moving from one place to another and back - with the clock moving, the cycling thing won't move all the way back). The slower you move the clock, the closer these cycles are to being complete round trips. Infinitely-slow clock transport, if it was possible, would involve complete round trips for each cycle.
Post by: Bored chemist on 05/08/2017 18:57:03
My cousin lives in France, I live in England.
If someone asks us "what's the name of the Capital city" we will give different answers- but nobody is being "fooled" are they?
Post by: David Cooper on 05/08/2017 23:00:43
It's not that anyone is wrong. it's a different point of view.
My cousin lives in France, I live in England.
If someone asks us "what's the name of the Capital city" we will give different answers- but nobody is being "fooled" are they?
They're answering different questions, just as they would if asked for the name of their mother. The issue with relativity is really very simple. If light is passing you at c relative to you and you then accelerate towards it, it cannot still be passing you at c relative to you. Anyone who believes it can be is buying into magic rather than science. The only model that can get round this issue is the eternal static block universe model where light has no speed as nothing moves at all, but that model also depends on magic for its existence because it can't account for how it was generated without switching to different laws of physics including an absolute frame of reference and Newtonian time.
Post by: Bored chemist on 06/08/2017 09:17:46
They're answering different questions,Fine.
The two questions being asked are what's the one way speed of light as BC determines it and what's the one way tipped of light as BC's cousin determines it.
Why would you expect the answers to always agree?
Post by: jeffreyH on 06/08/2017 09:45:21
Post by: David Cooper on 06/08/2017 19:58:12
They're answering different questions,Fine.
The two questions being asked are what's the one way speed of light as BC determines it and what's the one way tipped of light as BC's cousin determines it.
Why would you expect the answers to always agree?
The questions being asked are, what's the apparent one-way speed of light relative to the apparatus as BC determines it based on the assumption that he isn't moving and setting up his apparatus to measure it as c, and what's the apparent one-way speed of light relative to the apparatus as BC's cousin determines it based on the assumption that he isn't moving and setting up his apparatus to measure it as c. Obviously they will both come up with the answer c, but at least one of them is not measuring the one-way speed of light relative to them.
Post by: dutch on 06/08/2017 20:45:23
If a clock runs slow because it's moved, it fails to record all the time that has passed for it, and that results in an error in its timing. The faster you move it, the bigger that error is.
The difference is in the rate the clocks tick. It's still not an error because the amount of time that passed for the clock is exactly the number the clock reads. All clocks work the same down to the subatomic scales (in every experiment ever done). I know exactly what you're trying to say but calling it an "error" is just wrong.
Quote
it fails to record all the time that has passed for it
The above is especially wrong. The time that's passed for it is exactly equal to what its clock reads (proper time). The clock is measuring the number of ticks that take place and there is no error for a moving clock. Clocks moving relative to an absolute rest frame would simply tick slower. This slower tick rate is no more invalid than the faster tick rate of "stationary" clocks.
E.g. IF the system is stationary, THEN a clock moving through the system runs slow. While we are discussing things under that condition ("IF the system is stationary"), everything said is governed by that condition. When we switch to a different condition such as "IF the system is moving at 8.866c", everything we then say is governed by that new condition. The fact that we can't tell which of the cases is true does not negate the truth (conditional truth) of what is said about that case on the basis that it's true if the condition is true and may not be true if the condition is false.
I tend not to believe the "block universe" model but it's still mathematically valid. Your logic is only true from the 3D LET perspective and is not true from a completely 4D "block" perspective. The reason why LET and SR still both remain valid is because we can't set ε absolutely to distinguish the two. The two certainly use a CONVENTION or an agreed upon set of rules to explain what ε is. This convention goes beyond simply setting a single reference frame. However, for the last 110 years countless geniuses arguing fiercely have not set ε in a theory beyond using a convention.
You keep pushing that LET or some version of it must be true and SR's 4D concept is wrong. I personally tend to not like the fully 4D conceptualization of SR but I don't need to choose between LET and SR here. All I need to do is show that ε is chosen arbitrarily. I've done this multiple times.
The Bored chemist keeps saying from his perspective he could measure c one-way. However, his perspective is chosen by assuming ε =1/2 then he makes his measurement (completely circular reasoning). He couldn't offer one shred of proof that ε =1/2 and he simply chooses it by CONVENTION. I could do the same thing while choosing ε =1/4.
Even the idea that ε ≠ 1/2 means that you're moving at velocity v is assumed via convention.
It's the choice of frame that selects a proposed one-way speed of light relative to the system.
OK. And theories like SR and LET simply set up ε and therefore "choice of frame" via convention. The entire way they view ε is through convention.
You choose a frame of reference and thereby conditionally assert that the speed of light is the same relative to that frame in all directions. That makes the speed of light not equal to c relative to objects moving through that frame in most directions and provides a different theory as to the reality of the situation to any of the theories based on using different frames (all of those theories being in contradiction of each other as only one of them can be true).
Yes, one (or at least one convention) is most definitely right and all others are probably wrong. However, we have no way to prove what ε is so we simply create theories that form an agreed upon way to choose ε. These agreements are called conventions. The agreements are not called reference frames.
You choose a frame of reference and thereby conditionally assert that the speed of light is the same relative to that frame in all directions. That makes the speed of light not equal to c relative to objects moving through that frame in most directions and provides a different theory as to the reality of the situation to any of the theories based on using different frames (all of those theories being in contradiction of each other as only one of them can be true).
In a completely 4D universe you can still have ε =1/2 for all frames and have them all right locally. In a 3D LET framework it can't work. I know you don't like the fully 4D concept and I don't like it either but I'm not going to argue against its math. However, Einstein still set ε to a certain value arbitrarily in his theories.
If you restrict yourself to ε=1/2, you are selecting the frame of reference in which the system is at rest, and that sheds no light on anything. It's only when you work things through using at least two different reference frames that you can gain a real understanding of what's going on.
Einstein locally chose ε=1/2 and reference frames moving at velocity v relative to any point are seen as "rotated" in a 4D structure in the fully 4D conceptualization. ε appears to be something other than 1/2 when using the Lorentz Transformation (which comes from LET) but it does not in the fully 4D structure. This is similar to how a car would look shorter when its going up a steep hill when viewed from above. However, the car is not truly shorter. Again you can choose to believe either SR or LET as both match every experiment ever done (either can extend to a general theory). SR is easier to work with because its just simpler to assume ε=1/2 as a convention.
You keep saying I'm obfuscating things. However, I'm simply not trying to get a simple question bogged down by a pro LET or pro SR sideshow.
The simple answer:
We can ONLY measure the one-way speed of light via an arbitrarily set convention because we arbitrarily set ε.
Post by: David Cooper on 06/08/2017 23:54:38
If a clock runs slow because it's moved, it fails to record all the time that has passed for it, and that results in an error in its timing. The faster you move it, the bigger that error is.
The difference is in the rate the clocks tick. It's still not an error because the amount of time that passed for the clock is exactly the number the clock reads. All clocks work the same down to the subatomic scales (in every experiment ever done). I know exactly what you're trying to say but calling it an "error" is just wrong.
It's what you've just said that's wrong because you're assuming that the amount of time that's passed for the clock is equal to the amount of time it's recorded. When a light clock is stationary, it ticks at maximum speed because the round trip distance is shortest. When you move it, the round trip distance increases, so the clock records fewer cycles in a given length of time. If you move a clock backwards and forwards at the right frequency and with the right timing, you can shorten the round trip for the light and make the clock tick faster than normal, but again it is not recording the amount of time that has passed for it as it is exaggerating the amount of time that has gone by. Move it backwards and forwards a different way and you can make it record less time passing than has actually passed. Any movement of a clock leads to an error in the amount of time it records. Why would anyone be fooled by one kind of failure for a clock to record the right amount of time that's passed for it while not being fooled by another? In all cases, the light is moving at the same speed through space without being slowed by any kind of slowing of time.
Here's another case that shows up the truth. Imagine a powerful distant source of gamma rays that damages DNA. Perpendicular to the direction these rays are coming, we run the twins "paradox" experiment, having one twin travel at very high speed and the other travel slowly. Both are exposed to the same amount of radiation, and the moving twin has interacted with it with greater intensity throughout. That twin can be "younger" but genetically more damaged. This business of him supposedly being younger is really no different from putting some food in the freezer while identical food rots outside the freezer and then claiming on defrosting the food from the freezer that it's younger. It isn't - it's merely had its functionality slowed and has decayed less.
Quote
Quoteit fails to record all the time that has passed for it
The above is especially wrong. The time that's passed for it is exactly equal to what its clock reads (proper time). The clock is measuring the number of ticks that take place and there is no error for a moving clock. Clocks moving relative to an absolute rest frame would simply tick slower. This slower tick rate is no more invalid than the faster tick rate of "stationary" clocks.
The light in the light clock which has recorded less time has travelled the same distance as the light in the clock that was stationary. Time wasn't slowed for the moving clock - it merely took more time for it to complete each tick due to the lengthened cycle distance. Why would you be taken in by slowed functionality? We understand exactly how the functionality is slowed, so it's daft to ignore that understanding and to assert instead that time has slowed for anything. All that has slowed is the rate of cycle completions.
Quote
tend not to believe the "block universe" model but it's still mathematically valid. Your logic is only true from the 3D LET perspective and is not true from a completely 4D "block" perspective.
There are eight different models worthy of mention, four of them being 3D and four being their 4D equivalents. (Other models are possible beyond the eight, but they are always either obfuscated versions of the eight which can be written off as a result or they are equivalent models with extra dimensions added for no relevant gain.) Two of the eight models are static eternal blocks which were never generated in past to future order because the future was always pre-existing, so all the apparent causation tied up in their content is rendered fake, meaning that they instead depend on so much luck to account for their state that they are actually relying on magic. The other six models can optionally involve block universes too, but, if they do, they are attempting to account for the generation of the block rather than doing imaginary physics inside the block after all the construction-phase has been completed. One pair of these models moves all objects through time in such a way that no clocks run slow, but that results in event-meshing failures which again disqualify these models (or require extra complexity to be brought in to tolerate and correct those failures, which requires a changing history of events at individual Spacetime locations under Newtonian time). The remaining four models come in two pairs, one pair producing infinite numbers of contradictions (which leaves them relying on magic for their functionality) and the other pair eliminating the contradictions by having an absolute frame. With this last pair, one of them has a time dimension which adds no useful functionality over the model that uses Newtonian time alone, but both are viable.
Quote
The reason why LET and SR still both remain valid is because we can't set ε absolutely to distinguish the two.
They do not both remain valid - all SR models have either been shown not to function in a viable manner, or in the case of the static block model have been shown to lack real causation because no effects have can have been caused by their apparent causes.
Quote
The two certainly use a CONVENTION or an agreed upon set of rules to explain what ε is. This convention goes beyond simply setting a single reference frame. However, for the last 110 years countless geniuses arguing fiercely have not set ε in a theory beyond using a convention.
How does it go beyond choosing a frame of reference?
Quote
You keep pushing that LET or some version of it must be true and SR's 4D concept is wrong. I personally tend to not like the fully 4D conceptualization of SR but I don't need to choose between LET and SR here. All I need to do is show that ε is chosen arbitrarily. I've done this multiple times.
I don't say that the 4D concept is wrong - I say that two versions of it are viable, but one of them has to be able to tolerate event-meshing failures and the other has to have an absolute frame whose Newtonian time coordinates the slowing of any clocks regarded as being at rest in other frames.
Quote
OK. And theories like SR and LET simply set up ε and therefore "choice of frame" via convention. The entire way they view ε is through convention.
Well, it's fine for you and others to call it a convention, but that isn't as clear in meaning as describing it as choosing a frame of reference to use as the base for the analysis.
Quote
Yes, one (or at least one convention) is most definitely right and all others are probably wrong.
That claim is not compatible with SR where there is asserted to be no absolute frame. If it was accepted by the SR camp, we wouldn't be arguing about anything.
Quote
However, we have no way to prove what ε is so we simply create theories that form an agreed upon way to choose ε. These agreements are called conventions. The agreements are not called reference frames.
They are selections of convenient reference frames.
Quote
In a completely 4D universe you can still have ε =1/2 for all frames and have them all right locally. In a 3D LET framework it can't work. I know you don't like the fully 4D concept and I don't like it either but I'm not going to argue against its math. However, Einstein still set ε to a certain value arbitrarily in his theories.
You can only do away with it in a model that is so broken that real causality is eliminated.
Quote
Einstein locally chose ε=1/2 and reference frames moving at velocity v relative to any point are seen as "rotated" in a 4D structure in the fully 4D conceptualization. ε appears to be something other than 1/2 when using the Lorentz Transformation (which comes from LET) but it does not in the fully 4D structure. This is similar to how a car would look shorter when its going up a steep hill when viewed from above. However, the car is not truly shorter. Again you can choose to believe either SR or LET as both match every experiment ever done (either can extend to a general theory). SR is easier to work with because its just simpler to assume ε=1/2 as a convention.
Any change in frame of reference involves changing the speed of light across objects relative to those objects, and this applies in the 4D models just as in the 3D ones. It's only in the static block that you have the illusion of it working because nothing is moving at all. Go to the construction phase instead and then look at the speed of light relative to objects and you find a different story.
Quote
You keep saying I'm obfuscating things. However, I'm simply not trying to get a simple question bogged down by a pro LET or pro SR sideshow.
The simple answer:
We can ONLY measure the one-way speed of light via an arbitrarily set convention because we arbitrarily set ε.
Which is no different from saying that you're selecting a frame of reference and then using the assumption that light moves relative to it at c as a basis for measuring the speed of light as c. Of course, if you move a clock very slowly, you hide from yourself the fact that you're choosing a specific frame of reference if you don't understand how the time it's recording is going out of sync with the time recorded by the other clock, and that's the important thing here that needed to be explained.
Post by: dutch on 07/08/2017 01:47:03
It's what you've just said that's wrong because you're assuming that the amount of time that's passed for the clock is equal to the amount of time it's recorded. When a light clock is stationary, it ticks at maximum speed because the round trip distance is shortest. When you move it, the round trip distance increases, so the clock records fewer cycles in a given length of time. If you move a clock backwards and forwards at the right frequency and with the right timing, you can shorten the round trip for the light and make the clock tick faster than normal, but again it is not recording the amount of time that has passed for it as it is exaggerating the amount of time that has gone by. Move it backwards and forwards a different way and you can make it record less time passing than has actually passed. Any movement of a clock leads to an error in the amount of time it records. Why would anyone be fooled by one kind of failure for a clock to record the right amount of time that's passed for it while not being fooled by another? In all cases, the light is moving at the same speed through space without being slowed by any kind of slowing of time.
The time a clock measures is due to its internal ticking. In LET moving reference frames are just as valid as stationary ones to those observers so moving clocks work just as well. Sure their ticking is slowed relative to the absolute rest frame in LET but they otherwise function the same. They measure the time as it shows on the clocks just like clocks in the "rest frame" do and they match every other comoving clock. The "rest frame" in LET could have a uniform gravitational field in the entire observable universe making the clocks tick slower in our corner of the greater universe. This would not negate the fact that the clocks we have do measure something very real. They measure the local time (proper time).
Here's another case that shows up the truth. Imagine a powerful distant source of gamma rays that damages DNA. Perpendicular to the direction these rays are coming, we run the twins "paradox" experiment, having one twin travel at very high speed and the other travel slowly. Both are exposed to the same amount of radiation, and the moving twin has interacted with it with greater intensity throughout. That twin can be "younger" but genetically more damaged. This business of him supposedly being younger is really no different from putting some food in the freezer while identical food rots outside the freezer and then claiming on defrosting the food from the freezer that it's younger. It isn't - it's merely had its functionality slowed and has decayed less.
Like I've shown a dozen times on this thread:
t'/t = f'/f = (1 - v/c) / γ = γ / (1 + v/c) = (1 - a/c) / (1 + b/c) γb/γa where v = (a + b) / (1 + a b /c²)
The frequency f' is symmetric. The same thought experiment you have above must also work if most of the stuff in the universe was moving relative to the absolute rest frame while the twin was not. In this case everything in the universe except the twin would be younger but the twin would still be fried because f' would still be the same. Your thought experiment does not work because t', f', and energy are symmetric between reference frames. All observables are symmetric between reference frames so no thought experiment like this works. Your thought experiment shows that moving towards something blueshifts the light and away redshifts the light. This would be readily apparent to a 19th century physicist and anyone who studies the Classical or Relativistic Doppler Shift.
Quote
This business of him supposedly being younger is really no different from putting some food in the freezer while identical food rots outside the freezer and then claiming on defrosting the food from the freezer that it's younger. It isn't - it's merely had its functionality slowed and has decayed less.
Except if you were to go to bed and I would freeze you solid or even significantly lower you body temperature that would be very noticeable to everyone. If you were on a spacecraft and it accelerated slowly while you slept you would be able to act normally when you woke up.
Quote
All that has slowed is the rate of cycle completions.
If I take every kind of clock I could imagine and put them in a room. Next I find they all tick proportionally to each other in all experiments I could do if they're not accelerating relative to each other (the higher frequency clocks ticking faster allowing for a more accurate measurement). You know how I would define time? I would define it by the ticks of my clocks. Even in an absolute rest frame time is still measured by the ticking of clocks.... I don't know how you're defining time. Sure, I got it in LET that there's a frame where the ticks are locally the fastest. OK. So?
Quote
They do not both remain valid - all SR models have either been shown not to function in a viable manner, or in the case of the static block model have been shown to lack real causation because no effects have can have been caused by their apparent causes.
I know others would disagree. I know you don't like SR got it.
Quote
Quote
Yes, one (or at least one convention) is most definitely right and all others are probably wrong.
That claim is not compatible with SR where there is asserted to be no absolute frame. If it was accepted by the SR camp, we wouldn't be arguing about anything.
That's why you don't understand what a convention is. SR uses a convention to arbitrarily set ε =1/2 locally for all reference frames. This is ONE convention and SR sets ε by this one convention (we must believe in a truly 4D spacetime to do this). LET also sets ε by one convention but we must arbitrarily set the absolute rest frame (or absolute foliation in a general LET to do this).
Quote
It's only in the static block that you have the illusion of it working because nothing is moving at all
OK. So it works for the static block......... You're dragging this into a pro LET / pro SR debate again.
Quote
Which is no different from saying that you're selecting a frame of reference and then using the assumption that light moves relative to it at c as a basis for measuring the speed of light as c.
But you don't understand what a convention is.
Post by: guest4091 on 07/08/2017 16:50:31
I originally thought you understood spacetime drawings. If you don't, study this one, and the short math example.
It shows that regardless of setup, you will only measure light speed as c.
If you assume a rest frame for yourself, you accept the equality of out and back transit times.
https://app.box.com/s/z84l6wbpm4b291ve47i911ijnear6uqj
Post by: Bored chemist on 07/08/2017 20:19:05
regardless of setup, you will only measure light speed as c.If every possible experiment I could do to measure my mass indicated that it's about 70 Kg, would it be reasonable to conclude that my mass is about 70 Kg?
What's the difference between saying " no matter what the setup, you will always measure the speed of light as C"
and
" The speed of light is C"
?
Post by: David Cooper on 07/08/2017 22:41:45
The time a clock measures is due to its internal ticking. ... They measure the local time (proper time).
None of which negates the fact that they fail to record all the time that's passing for them if they're moving (and if they're in a gravitational field) and that the times they record are therefore out by an error.
Quote
The same thought experiment you have above must also work if most of the stuff in the universe was moving relative to the absolute rest frame while the twin was not. In this case everything in the universe except the twin would be younger but the twin would still be fried because f' would still be the same.
The moving twin may well be stationary on one leg of the tirp, but will then be moving at much higher speed on the other leg of the trip and will always end up "younger" than the stay-at-home twin, but the events involving encounters with gamma rays have continued at a high rate which do not speak of a slowing of time for the moving twin at all. Another experiment could put one twin near to a black hole and send the same radiation through them from a distant source - again the "younger" one can be more damaged at the end of the process, and indeed, the more extreme the reduction in growth ageing, the more extreme the overall damage will be.
Quote
Except if you were to go to bed and I would freeze you solid or even significantly lower you body temperature that would be very noticeable to everyone. If you were on a spacecraft and it accelerated slowly while you slept you would be able to act normally when you woke up.
Different methods of slowing functionality have different side-effects, and some have none, but the key point is that time is not being slowed. Cycles are being slowed. Functionality is being slowed. To say that time is slowed is taking a step into the irrational.
Quote
Even in an absolute rest frame time is still measured by the ticking of clocks.... I don't know how you're defining time.
No - that's a bad definition. Time should never be defined by cycle counters when the cycle length can lengthen without time running slow.
Quote
QuoteThey do not both remain valid - all SR models have either been shown not to function in a viable manner, or in the case of the static block model have been shown to lack real causation because no effects have can have been caused by their apparent causes.
I know others would disagree. I know you don't like SR got it.
Liking or disliking things doesn't come into it. It's about what is possible within the bounds of reason, and those people who think they have an SR model that works viably are badly mistaken. No SR model functions rationally - the one that comes closest to appearing to function properly (without adding features not specified [or banned] in the model description) can only account for imaginary physics in a static block where there is never any movement or change at all, and that means the model in completely incapable of accounting for causality as it gives it no room whatsoever to operate - no effects in this model can be caused by their apparent causes. Those who believe the static block model is sufficient are fantasists.
Quote
That's why you don't understand what a convention is. SR uses a convention to arbitrarily set ε =1/2 locally for all reference frames. This is ONE convention and SR sets ε by this one convention (we must believe in a truly 4D spacetime to do this). LET also sets ε by one convention but we must arbitrarily set the absolute rest frame (or absolute foliation in a general LET to do this).
I see, so you don't call it selecting a frame of reference in the 4D models even though it's still selecting a frame of reference.
Quote
QuoteIt's only in the static block that you have the illusion of it working because nothing is moving at all
OK. So it works for the static block......... You're dragging this into a pro LET / pro SR debate again.
No, it doesn't work for the static block - it merely gives the illusion of working. It's a broken model that has no way of generating the block without switching to different laws of physics.
Quote
But you don't understand what a convention is.
A convention can be many things, but in this case it clearly means selecting a frame of reference.
One important point to look at though is what happens to the speed of light in those 4D models where movement is possible and causality can be real. In all of these models light shrinks every single path it takes to zero length and it therefore has no speed at all. In one of the 4D models where "time" never runs slow for any clocks, that means that light travels the whole way from the start of the universe (timewise) to the end in an instant, failing along the way to interact with any of the objects it's supposed to encounter because they aren't there yet as it takes them longer to reach the same Spacetime loactions (longer under a Newtonian time which must be brought into the model to make it possible for clocks never to run slow relative to each other). In the other 4D models, light covers all its zero-length paths in >0 lengths of Newtonian time (which again isn't part of SR but has to be brought in to make the models function viably). The amount of time (of the Newtonian variety) that it takes to cover any given path will vary though depending on the frame of reference chosen to govern the running of the model. The SR models have all been shown to be incapable of generating a real universe without bringing in Newtonian time and a frame of reference to coordinate the unfolding of events, and it's high time people pushing SR's dogma woke up to the fact that their models are broken and dysfunctional. What they do though is point at different incompatible broken models to account for different aspects of the universe while they make out that they have a single viable model. They are experts in self delusion. The only viable models are radical departures from SR.
Post by: guest4091 on 08/08/2017 18:30:33
" The speed of light is C"I'm agreeing with you, and on the basis of a degree of synchronization that presents no significant difference. We can't use the ideal conditions, we don't have ideal clocks. I'm also discouraging anyone with a complex or simple setup thinking they can somehow circumvent the light postulate.
?
Post by: Bored chemist on 08/08/2017 18:43:43
OK from the PoV of a passing astronaut, I get the wrong answer- but his view of everything would be different.
Certainly, the expression here for the error in timekeeping
https://en.wikipedia.org/wiki/Time_dilation#Simple_inference_of_velocity_time_dilation
tends to zero for slow transport of the clock.
So I should be able to have two clocks, separated in space, but still essentially synchronised.
I can record when a flash of light reaches them.
And if one is "near" and the other "far" from the flash I can establish a time difference, and a distance difference.
Post by: David Cooper on 08/08/2017 23:42:46
Certainly, the expression here for the error in timekeeping
https://en.wikipedia.org/wiki/Time_dilation#Simple_inference_of_velocity_time_dilation
tends to zero for slow transport of the clock.
It only tends to zero for one frame of reference. For all other frames, it tends to a different value, but we're talking about a hidden error, so you can't detect whether it applies to your frame or not. If you happen to be stationary and move your clock into position very slowly, your clocks will remain almost exactly in sync, but if you happen to be moving at very high speed instead, the further you move the clock, the further out of sync the two clocks will become (and you won't notice because they'll always look in sync to you as you move along with them, which means you'll always think the error tends to zero for you even when it doesn't in the underlying reality). The result will be that you record the speed of light from one clock to the other as c no matter how long it really takes the light to make that trip.
Post by: dutch on 09/08/2017 19:16:49
I'm quite happy to accept that I'm wrong, but nobody seems to have come up with a viable reason yet.
OK from the PoV of a passing astronaut, I get the wrong answer- but his view of everything would be different.
Certainly, the expression here for the error in timekeeping
https://en.wikipedia.org/wiki/Time_dilation#Simple_inference_of_velocity_time_dilation
tends to zero for slow transport of the clock.
So I should be able to have two clocks, separated in space, but still essentially synchronised.
I can record when a flash of light reaches them.
And if one is "near" and the other "far" from the flash I can establish a time difference, and a distance difference.
Say you've got 100 red and green apples and only a blind man can count all of them. The blind man confirms there's 100 apples. You also know at least one apple is red and at least one apple is green.
The equation: R + G = 100 R and G are integers > 0
You could set R = 1/2 G and use this convention for all apple counts. You could even claim this is your "point of view." If the blind man counts 500 apples you could proclaim 250 of them are red and 250 are green.
Because we can't get any more information than the total count and the fact that we know at least one apples is red or green we would never be wrong to our knowledge to use the convention R = 1/2 G. However, R = 4 G is also valid as is any R = α G for all α where both R and G form integers > 0.
In this case of R = 4 G and R + G = 100, G = 20 and R = 80.
We can confirm the two-way speed of light and get everyone to agree on it (barring GR curvature). There's math that allows the one-way speed of light to take on any value from 1/2 to ∞ relative to a reference frame. We have nothing absolute to set our clocks to that we can find. We can select ANY valid value for c- and c+.
The valid values relative to our reference frame are:
c± = 1/(1 ± κ) where κ any value 0 to 1
Attributing ε =1/2 to "our point of view" of our own reference frame is a CONVENTION. A standardized agreed upon way to apply ε (that goes beyond choosing a reference frame). LET agrees to apply a different ε to each reference frame absolutely as shown in the Lorentz Transformation (forming an absolute rest frame where ε =1/2 only in one frame; with LET there's an infinite number of different possible conventions) and SR/GR agrees to locally apply ε =1/2 to all reference frames (seemingly requiring a 4D block universe to work). Within a convention you can measure the one-way speed of light exactly (for LET you need to know the absolute rest frame) but this convention may or may not be correct. The value for the one-way speed depends on convention.
The one-way speed of light is simply impossible to measure without applying an arbitrary convention by any known means.
Post by: Bored chemist on 09/08/2017 21:37:26
"But m'lord, from my point of view, the car was stationary; the police helicopter caught up with me so, from his point of view I was actually going backwards and so it's only from the unique perspective of the arresting officer that I was actually doing more than 70 MPH".
"Yes- but his is the viewpoint that counts"
Any two items in relative motion are moving- or not- depending on your point of view.
So, almost nothing has a well defined speed - it's always a matter of viewpoint.
For light it's different- everyone measures the speed as C.
Now there's this strange world where I say that I can measure the speed of light as it makes a one-way trip. And I explain how.
And I get the answer C
And you tell me it's wrong, because someone else- who is moving- would disagree.
Well, how is that different from, for example the points of view of the police and me, giving rise to different views on the speed of my car?
Of course it's an arbitrary point of view.
All measurements of speed are based on an arbitrary point of view.
So, as you say:
The one-way speed of
Post by: dutch on 10/08/2017 00:17:56
"Yes- but his is the viewpoint that counts"
Any two items in relative motion are moving- or not- depending on your point of view.
So, almost nothing has a well defined speed - it's always a matter of viewpoint.
For light it's different- everyone measures the speed as C.
If I define the "velocity" v of an object with mass as a certain f'/f (= t'/t = (E'/h)/(E/h)) it is symmetrically defined between any two reference frames. It's an observable between reference frames. We can use a radar gun to define the speed of another object as v via f'/f and that other object will also report the same exact v because the Doppler Shift is symmetric. It doesn't matter what reference frame or convention you choose you'd expect the same f'/f. If the cop has a 500 MHz light source and it shifts to 499.9 MHz then the same thing would happen to your light source. When you collide with the cop both will agree on how severe the impact was.
Light does not Doppler Shift itself but rather there is a Doppler Shift from source to receiver. The source and receiver are objects with some mass m. This Doppler Shift is symmetric (Doppler shift is independent of which one's the source) REGARDLESS of convention or reference frame choice.
Again...
Quote
Like I've shown a dozen times on this thread:
t'/t = f'/f = (1 - v/c) / γ = γ / (1 + v/c) = (1 - a/c) / (1 + b/c) γb/γa where v = (a + b) / (1 + a b /c²)
The absolute round trip speed of light c is VERY well defined for everyone. The velocity v between two objects when defined by a certain f'/f = (E'/ h)/(E/ h) is also well defined and symmetric by anyone's viewpoint.
An absolute speed of an object isn't defined without convention and neither is the one-way speed of light. You can use the very observable Doppler Shifts to define a very non-arbitrary v between any two objects.
If you Doppler Shift from point X to Z through Y via the below (let X to Y =a and Y to Z = b)
f (1 - a/c) / γa * (1 - b/c) / γb
The above is exactly the same as
f (1 - v/c) / γv = f (1 - a/c) / γa * (1 - b/c) / γb
Solve for v
v = (a + b) / (1 + a b /c²) = Relativistic Velocity Addition Formula
This v is defined not by how long it takes to get from point A when the clock starts to point B when the other clock stops but rather by the shift in frequency, observable shift in t', and therefore the shift in energy.
We cannot pin down the absolute start time nor the absolute end time for ANY spatially separated clocks at all. We can only choose one via convention but we can pin down the shift in frequency and shift in energy.
Quote
"But m'lord, from my point of view, the car was stationary; the police helicopter caught up with me so, from his point of view I was actually going backwards and so it's only from the unique perspective of the arresting officer that I was actually doing more than 70 MPH".
Everyone can agree on the shift in frequency between the ground and the car. Defined this way we have a definite v. We can't say in an absolute sense when the car started its journey or ended it (or if there is or isn't an absolute time). A traditional view of velocity where we don't choose a convention needs to know these values. However, we can define f'/f, t'/t, and E'/E.
The light may have frequency ratio f'/f in one direction but it may take 1 million years to make a certain journey (from another perspective we could choose or a hidden absolute rest frame). In the other direction it may also have frequency f'/f but it takes only an instant to make the journey. Defining v with f'/f is really measuring a two-way speed. The v we measure is also a very real two-way speed. I never claimed the constant c wasn't exactly defined nor did I ever say a "v" couldn't be exactly defined. However, both are only defined without choice of convention two-way.
Trying to measure frequency shift (f'/f -1), energy shift (E'/E -1), momentum shift (k'/k -1), observable time shift (t'/t-1) is EXACT. Trying to pin down what "now" is for two spatially separated clocks is only done via convention. Without knowing what now is in two different locations (and we can't; Relativity is a local theory) we have NO idea what a one-way speed is in the classical sense. Many have stated "now" is a meaningless concept in the physics we can run experiments on unless you're discussing a "now" at a single event.
Define v as:
v = c (1 - (f’/f)²) / (1 + (f’/f)²) frequency
or v = c (1 - (E’/E)²) / (1 + (E’/E)²) energy
or v = c (1 - (t'/t)²) / (1 + (t’/t)²) time
or v = c (1 - (κ’/κ)²) / (1 + (κ’/κ)²) wavenumber
or v = c (1 - (x’/x)²) / (1 + (x’/x)²) distance
or v = c (1 - (ρ’/ρ)²) / (1 + (ρ’/ρ)²) momentum
All the above three are defined with "two-way" measurements.
Post by: dutch on 10/08/2017 18:57:06
c± = c / (1 ± κ) for κ = 0 to 1
t = ½ ( x/c- + x/c+) = x/c → two-way speed of c
Define v+ as:
v+ = c/(1 + κ) (1 - (f’/f)²) / (1 + (f’/f)²) frequency
or v+ = c/(1 + κ) (1 - (E’/E)²) / (1 + (E’/E)²) energy
or v+ = c/(1 + κ) (1 - (t'/t)²) / (1 + (t’/t)²) time
or v+ = c/(1 + κ) (1 - (κ’/κ)²) / (1 + (κ’/κ)²) wavenumber (non-angular wavenumber k = 1/λ)
or v+ = c/(1 + κ) (1 - (x’/x)²) / (1 + (x’/x)²) distance
or v+ = c/(1 + κ) (1 - (ρ’/ρ)²) / (1 + (ρ’/ρ)²) momentum
Define v- as:
v- = c/(1 - κ) (1 - (f’/f)²) / (1 + (f’/f)²) frequency
or v- = c/(1 - κ) (1 - (E’/E)²) / (1 + (E’/E)²) energy
or v- = c/(1 - κ) (1 - (t'/t)²) / (1 + (t’/t)²) time
or v- = c/(1 - κ) (1 - (κ’/κ)²) / (1 + (κ’/κ)²) wavenumber (non-angular wavenumber k = 1/λ)
or v- = c/(1 - κ) (1 - (x’/x)²) / (1 + (x’/x)²) distance
or v- = c/(1 - κ) (1 - (ρ’/ρ)²) / (1 + (ρ’/ρ)²) momentum
For example:
f'/f = (1-0.99)/(1-0.99^2)^0.5 = .070888
v = (1 - (f’/f)²) / (1 + (f’/f)²) = .99
Let κ = .6
(1 - (f’/f)²) / (1 + (f’/f)²) /(1+0.6) = .61875 = v+
(1 - (f’/f)²) / (1 + (f’/f)²) /(1-0.6) = 2.475 = v-
t (two-way trip)= 1/2 * ( x/v+ + x/v-) = 1/2 * ( x/.61875 + x/2.475) = 1.010101 x
velocity = distance/time = x/t
1/1.010101 = v = .99
The v is the well-defined round trip average speed by ANYONE'S perspective (assuming a relatively flat region of spacetime). We can assume ε = 1/2 where κ =0 if we wish to simplify the math. This is just a convention, nevertheless the value v as a two-way average is very real for all perspectives.
There is a whole lot of symmetry going on here. HOWEVER, nothing tells us the one-way speed. We only assume it.
Post by: Bored chemist on 10/08/2017 19:19:20
So,
How do I determine the one way speed of Usain Bolt?
I look forward to being told this is impossible.
Post by: dutch on 11/08/2017 04:43:56
On a related note, all the arguments put forward for my measurement of the one way tipped of light seem independent of the fact that it was light.
So,
How do I determine the one way speed of Usain Bolt?
I look forward to being told this is impossible.
Do you understand the math or what I wrote? Do you understand how I defined velocity?
And no you can't measure the one-way speed of anything without making assumptions. We don't know what "now" is somewhere else so we can only do two-way measurements. Did I ever say any different? This thread was about the one-way speed of light......
The below has three variables that give a v we can define and it's not that hard to understand.
v = c (1 - (f’/f)²) / (1 + (f’/f)²)
c is the well understood and directly measured two-way speed of light. Very few people dispute this value (unless they're wearing tin foil hats). f' is the output frequency of the Relativistic Doppler Shift which is symmetric regardless of viewpoint and we can locally measure the f' we receive from another reference frame. f is the frequency measured within one's own reference frame. f is locally measured and f' is symmetric regardless of viewpoint chosen (and locally measured). f and f' don't give any one-way information and neither does the two-way speed of light c.
We can define a very non-arbitrary v as I've done but it's NOT one-way. It's the average of the two-way speed. I already gave all the math for this.
Read this:
Quote
Although the average speed over a two-way path can be measured, the one-way speed in one direction or the other is undefined (and not simply unknown), unless one can define what is "the same time" in two different locations.
https://en.wikipedia.org/wiki/One-way_speed_of_light
Why are you going against physics? I've never heard of a rational well-educated physicists say anything other than the one-way speed of light (or anything) isn't defined without resorting to convention. Relativity is a LOCAL theory. One-way speeds are inherently non-local and they don't have any definite meaning. You are free to choose ε = ½ because either:
1) We can't tell what the right ε is but it doesn't matter in any experiments we've done so were free to choose.
2) ε actually is ½ so we're right. Good for us.
3) It simply doesn't matter because it doesn't have a true meaning.
Could it possibly be that Relativity showed us that we don't know what now is in two different locations? I thought this was old news. This means we can't measure the one-way speed of anything no matter how much we think we can. We do what we do best... we make useful shortcuts to rationalize the world and many don't easily see these shortcuts for what they are.
You keep on saying the same thing but you give no sources or math whatsoever.
Tell me where the math or logic is wrong... Give me some source or relativistic math that backs you up.
Post by: guest39538 on 13/08/2017 13:04:23
We don't know what "now" is somewhere else
Now here is the same now as somewhere else. Now is a universal simultaneous event always.
Einstein never considered the two way journey of light in his ideas . If he had , he would of known and realised that simultaneity is nothing to do with different now's or different rates of time.
In example lets look at the sun, it takes approx 8 minutes and 24 seconds for the light to travel distance X. We can say that we see the Sun 8 minutes 24 seconds after the first wave-packets have left the Sun.
However if we look at the reverse and simultaneous the events. The Light from us takes approx 8 minutes and 24 seconds to reach the Sun.
An observer on the Sun and the Earth in this instant observe each other at the same time. Now remains synchronous.
+ve=8 mins 24 seconds
-ve=8 mins 24 seconds
Vector analysis shows now remains synchronous , the present now is the present now of the entire Universe and always synchronous, regardless of Einsteins 1 way thinking and the mythology involved as the outcome of this.
Quote
This means we can't measure the one-way speed of anything no matter how much we think we can.
I disagree, using tP we could , it would be very accurate.
Post by: Bored chemist on 13/08/2017 14:33:58
you can't measure the one-way speed of anything without making assumptions.
OK, but we do it all the time- Mr Bolt being one of the better known examples.
So, using the same assumptions as we use in the 100 metres, can we measure the 1 way speed of light?
Re this- (which you asked me to read)
" unless one can define what is "the same time" in two different locations.".
I went to some lengths to define "the same time in two different locations.".
Did you not notice?
All that stuff about indefinitely slow bicycles and long flat roads?
Post by: dutch on 13/08/2017 16:02:26
Vector analysis shows now remains synchronous , the present now is the present now of the entire Universe and always synchronous, regardless of Einsteins 1 way thinking and the mythology involved as the outcome of this.
Quote
This means we can't measure the one-way speed of anything no matter how much we think we can.
I disagree, using tP we could , it would be very accurate.
Thebox... your entire analysis shows that you don't understand Relativity. Please read up on it. There's too many mistakes to correct.
you can't measure the one-way speed of anything without making assumptions.
OK, but we do it all the time- Mr Bolt being one of the better known examples.
Yes, that's the human condition to make assumptions all the time. So what? We make shortcuts to make our lives easier and often don't even realize it. How does this change the fact that we cannot measure the one way speed of light without convention? This is what I've said since the start.
Are you saying we can measure the absolute one-way speed of light? If so then you are very much wrong. We only measure the one-way speed of light via arbitrary convention.
Re this- (which you asked me to read)
" unless one can define what is "the same time" in two different locations.".
I went to some lengths to define "the same time in two different locations.".
Did you not notice?
All that stuff about indefinitely slow bicycles and long flat roads?
You aren't defining the "same time" in two different locations. You are assuming what the same time is in two different locations based on convention. Conventions don't define something absolute they are an agreement to assume something or some system as standard (like always choosing ε = ½ for your own point of view). Defining what the same time is in two locations would require you to know what absolute time is and absolute time may or may not exist. Definitions are definite and cannot rely on an arbitrary agreed upon convention.
Why can't I decide to use ε = ¼ for my own point of view? I get all the correct answers for everything observable but I have different one-way speeds.
All that stuff about indefinitely slow bicycles and long flat roads?
Do you really understand any of this? I don't care about slow bikes. If κ → 1 in the below:
v- = c/(1 - κ) (1 - (f’/f)²) / (1 + (f’/f)²) → v- = ∞ c (1 - (f’/f)²) / (1 + (f’/f)²)
v- → ∞ even if (f’/f)² goes arbitrarily close to one. Even a hair above/below one would still bring v- → ±∞.
"Slow" bikes simply don't matter.
Again you gave no math and no links to support your claims.
Post by: Bored chemist on 13/08/2017 16:25:27
Someone did that for us.
It's something to do with caesium atoms.
And the point is that (at least ideally) any caesium clock defines time locally exactly- by definition. (as long as nothing upsets it locally- if you happen to have a black hole in your lab, you need to allow for that- but even in that case, the clock is right, but only for its own position)
Now, we know that two clocks in different gravitational fields will tick at different rates. But then again, I said that (by the amusing magic of a thought experiment) we know that gravity is the same all across the experimental area.
We also know that moving clocks don't run at the right speed, but we know that the extent of that "wrongness" falls to zero if the speed is zero. (And, if we like, we can move them quickly, calculate the error, and allow for it).
So, since there's only one thing perturbing the clock, and we can make that perturbation as small as we like - and then allow for it- we do know when "now" is at a a distant location.
I know when the distant clock say 12 o'clock- because it's the same as when my local clock says 12 (give or take a small calculable correction which I can make as small; as I like, then allow for).
Post by: guest39538 on 13/08/2017 18:33:47
Vector analysis shows now remains synchronous , the present now is the present now of the entire Universe and always synchronous, regardless of Einsteins 1 way thinking and the mythology involved as the outcome of this.
Quote
This means we can't measure the one-way speed of anything no matter how much we think we can.
I disagree, using tP we could , it would be very accurate.
Thebox... your entire analysis shows that you don't understand Relativity. Please read up on it. There's too many mistakes to correct.
And quite clearly you do not understand reality, there is so many faults in relativity there is too many mistakes to correct. However you are not willing to listen to the mistakes. You want to continue the discussion blindly under some sort of subjective illusion. I am objective, you are not being objective at all. Please try to read up on reality , I have made enough posts about it.
Start with time, I have it correct, Einstein had it wrong. Please find appropriate thread.
Post by: dutch on 13/08/2017 19:22:01
And quite clearly you do not understand reality, there is so many faults in relativity there is too many mistakes to correct. However you are not willing to listen to the mistakes. You want to continue the discussion blindly under some sort of subjective illusion. I am objective, you are not being objective at all. Please try to read up on reality , I have made enough posts about it.
Start with time, I have it correct, Einstein had it wrong. Please find appropriate thread.
I know the limits to what I can absolutely say about reality in this case. OUR view is subjected to a convention because we can't pin down ε in experiments. Please tell me what ε I should apply, why, and prove to me its the only possible ε I could possibly apply. If you can't then at least our view is subjective. I've treated LET and SR equally in this thread. I don't care if you think Einstein's convention is right or wrong we are still free to use it (or not to use it). If you think differently please provide the experimental evidence.
I don't define the time at all.
Someone did that for us.
Unless it was God (and you can prove it) or an ε was experimentally proven then it doesn't matter. Einstein and his convention is not God nor does his choice of convention result from experiment. If it did it wouldn't be a convention.
It's something to do with caesium atoms.
How enlightening...........
And the point is that (at least ideally) any caesium clock defines time locally exactly- by definition. (as long as nothing upsets it locally- if you happen to have a black hole in your lab, you need to allow for that- but even in that case, the clock is right, but only for its own position)
Yes, you can define clocks locally. So? Relativity is a local theory.
We also know that moving clocks don't run at the right speed, but we know that the extent of that "wrongness" falls to zero if the speed is zero. (And, if we like, we can move them quickly, calculate the error, and allow for it).
By what convention do we know this? I gave you very clear math you fail to use.
So, since there's only one thing perturbing the clock, and we can make that perturbation as small as we like - and then allow for it- we do know when "now" is at a a distant location.
I know when the distant clock say 12 o'clock- because it's the same as when my local clock says 12 (give or take a small calculable correction which I can make as small; as I like, then allow for).
And how do you know what it says in some distant location without arbitrarily picking ε? Can you send a message to that location instantly? No? Go back and read my classical thought experiment with the Doppler Shift in this thread.
After we arbitrarily set ε then we can know the clock de-synchronization to any level our equipment allows. We still must choose first and our choice is circularly giving us the one-way value of c.
Post by: Bored chemist on 13/08/2017 19:53:11
By what convention do we know this? I gave you very clear math you fail to use.We know it buy observation. The "clock on a jet plane" experiment.
And how do you know what it says in some distant location without arbitrarily picking ε?
because it's a godforsaken clock. It's going to tell the same times as the local one because there's no reason for it not to, and that's what clocks do.
If you like I can (in this thought experiment,
Set my watch to the first clock, walk to the distant clock check that they agree (to an arbitrary degree of precision as long as I walk slowly enough, then walk back and check that my watch still agrees with the first clock.
The two clocks and my watch all stay arbitrarily close to synchronised (My watch, is, of course also a "perfect" clock.)
Post by: guest39538 on 13/08/2017 20:44:13
εYou are asking me what is epsilon? If I knew in what context you were asking , I might be able to provide an answer.
Quote
I don't care if you think Einstein's convention is right or wrong we are still free to use it (or not to use it). If you think differently please provide the experimental evidence.
You are free to use all the subjective thinking you like, however this will not give the objective answers . What error would you like me to show?
The problem all starts with time, an objective and logical truth about time shows relativity to be mostly a pile of rubbish.
Most of relativity is based on time, if the version of time collapses so does the after thought.
You know very well that time forward is directly proportional to time passed. You also know very well that time is continuous and not in discrete packets of 1.s increments. You also know very well that Einstein did not consider time passing at small increments such as time Planck (tP).
All this adds up to the conclusion that time can not slow down or speed up. Quite clearly relativity fails once the interpretation of time is corrected. I do not need a single experiment to show this. The explanation is logically a 100% axiom with no errors. My definition of time is 100% correct and an axiom
time: A quantifiable measurement directly proportional to change
p.s I did provide vector maths in which you ignored or do not have the knowledge to read. But in case you did not get it!
v=c
=1.s=1.s(a) and (b) observe each other simultaneous. i.e (a) now is always (b) now
=1.s=1.sIT IS NOT
from
and
c is directional proportional in t/dx
Post by: Bored chemist on 13/08/2017 21:25:51
The problem all starts with time, an objective and logical truth about time shows relativity to be mostly a pile of rubbish.
It works.
Post by: guest39538 on 13/08/2017 21:59:02
I never said it did not work, I would be more than happy to accept it all if the interpretation was correct. I.e the mechanics of relativity is timing and timing can slow down or speed up relative to the observers measurement.The problem all starts with time, an objective and logical truth about time shows relativity to be mostly a pile of rubbish.
It works.
p.s Of course Newtons absolute time would have to be brought back also , that would be correct. t=ΔtP
Post by: dutch on 13/08/2017 23:14:17
We know it buy observation. The "clock on a jet plane" experiment.
:o No... The Twins Paradox (tested with the "clock on a jet plane" experiment) requires a round trip and I already explained at length round trip average velocities are well-known and independent of our choice of ε. Two-way speeds don't tell us anything about a one-way speed. Did you completely miss all the equations?
We know t (our own time), we know t' (time observed via signal sent to us from another frame moving relative to us). We do NOT know τ (time dilation) without choosing an ε. Are you even attempting to understand the math?
Quote
Again...
Like I've shown a dozen times on this thread:
t'/t = f'/f = (1 - v/c) / γ = γ / (1 + v/c) = (1 - a/c) / (1 + b/c) γb/γa where v = (a + b) / (1 + a b /c²)
with the same t and t', τ/t= γb/γa where v = (a + b) / (1 + a b /c²) 0 < τ/t < ∞
because it's a godforsaken clock.
Great argument...
If you like I can (in this thought experiment,
Set my watch to the first clock, walk to the distant clock check that they agree (to an arbitrary degree of precision as long as I walk slowly enough, then walk back and check that my watch still agrees with the first clock.
The two clocks and my watch all stay arbitrarily close to synchronised (My watch, is, of course also a "perfect" clock.)
No... slow clock transport and light synchronization are identical. I do NOT... in ANY possible way care how slow you move the clocks. I already gave all the math for this. I even worked out examples of how the math works. Again what is your problem with the math? Why are you writing the same nonsense?
ε
You are asking me what is epsilon? If I knew in what context you were asking , I might be able to provide an answer.
It doesn't matter the context. Can you prove how to apply ε to every frame in a definitive way? If not.., then our view IS subjective regardless of whether you believe there is an objective reality behind the scenes (or what they reality looks like, "block universe or LET universe etc). Do you understand the concept that we humans don't know everything? When we don't know everything we often use conventions to fill in the gaps. It's OK to use conventions as long as we remember they're conventions.
You know very well that time forward is directly proportional to time passed. You also know very well that time is continuous and not in discrete packets of 1.s increments. You also know very well that Einstein did not consider time passing at small increments such as time Planck (tP).
All this adds up to the conclusion that time can not slow down or speed up. Quite clearly relativity fails once the interpretation of time is corrected. I do not need a single experiment to show this. The explanation is logically a 100% axiom with no errors. My definition of time is 100% correct and an axiom
time: A quantifiable measurement directly proportional to change
p.s I did provide vector maths in which you ignored or do not have the knowledge to read. But in case you did not get it!
v=c
=1.s
=1.s
(a) and (b) observe each other simultaneous. i.e (a) now is always (b) now
=1.s
=1.s
IT IS NOT
from
and
c is directional proportional in t/dx
Please stop embarrassing yourself.
Post by: guest39538 on 13/08/2017 23:28:16
Please stop embarrassing yourself.
I am not embarrassed about being correct. It is 100's of years of subjective belief that is the worlds embarrassment , not mine.
I know my vector analysis is correct. If you do not understand it then I suggest you learn something about analysis.
1=1 in any language . It is rather a huge embarrassment for all these years to not spot that time does not slow down or speed up. I am the one who discovered and explained this, I know what I have done.
p.s ε=0 and 1
Try my 3d energy charge matrix
charge matrix.jpg (23.52 kB . 1015x625 - viewed 4941 times)Post by: dutch on 14/08/2017 02:17:34
I am not embarrassed about being correct. It is 100's of years of subjective belief that is the worlds embarrassment , not mine.
Relativistic theories which include LET and Einstein's theory of SR/GR definitely work and match experiment. The world should not be embarrassed about this at all. The equations work to incredible accuracy. However, one has to look closely at the equations to remember that SR/GR utilize an arbitrary convention designed to simplify calculation (which is very helpful) and other theories also must use arbitrary conventions unless they prove a definitive way to apply ε to all reference frames.
Just because we humans can't identify an objective value of ε does not mean one does not exist. It could imply that we just don't know everything.
It is rather a huge embarrassment for all these years to not spot that time does not slow down or speed up.
Really? How do you define time? I define it by the ticks of clocks. What other experimentally viable way do you define time? Even if there is an absolute rest frame where clocks tick the fastest (and I'm not saying there isn't) how do YOU find it? If you can't find it definitively then what else but observable clocks define time? It you want to discuss time then you need to discuss some sort of clock.
I am the one who discovered and explained this, I know what I have done.
Really? Prove it to me.
1=1 in any language .
Are you trolling me? I want to get real and important points across but what I get back..............................
p.s ε=0 and 1
Why? Why does ε=0 and 1 at the same time? Prove it to me....
Post by: guest39538 on 14/08/2017 12:31:01
Really? How do you define time? I define it by the ticks of clocks
Ok. let us start here with your first mistake. The ticks of a clock define the measuring of time, the clock suppose to be an equal and equivalent measurement of time. However your clocks fail and are a variant measuring device. Counting time slow of fast does not change the ''speed'' of time. A clock and the tick is not time. The tick as the only use of the practitioner.
When you understand this I will move onto your other questions.
Do you understand the tick has nothing to do with time?
Post by: guest4091 on 14/08/2017 17:09:33
I have not seen any tables for td when slow transporting clocks.
Here is one to consider.
https://app.box.com/s/v722vkyrscqo4v5lye0j4nit05gglocy
Post by: Bored chemist on 14/08/2017 19:55:58
That is impossible if you understand relativity.It's possible if they are all in the same place.
(or, if you prefer, it's possible to get arbitrarily good synchronisation for small enough clocks.)
Are we in the solar system? How fast is the solar system spinning? Are we in a galaxy? How fast is the galaxy spinning? Are you going with the spin or against the spin? How do you determine not moving?
I solved that one earlier when I destroyed the rest of the universe (for the purposes of a thought experiment)
Post by: Bored chemist on 14/08/2017 20:00:32
Bored chemist;Thanks, that's the closest anyone has yet got to answering the question I asked several pages ago.
I have not seen any tables for td when slow transporting clocks.
Here is one to consider.
https://app.box.com/s/v722vkyrscqo4v5lye0j4nit05gglocy
I consider 30m/s (nearly 70MPH) rather fast for a bike.
I also considered continental drift as a possible transport mechanism...
Post by: Bored chemist on 14/08/2017 20:02:50
Please stop embarrassing yourself.I might not agree with Dutch about many things, but he's spot on with regard to Thebox.
Post by: guest39538 on 15/08/2017 10:38:19
What is embarrassing is adults on a science forum who carry on discussing fairy tales as if fact and reality. Now I know I do not fall into that category because I have a brain in my head.Please stop embarrassing yourself.I might not agree with Dutch about many things, but he's spot on with regard to Thebox.
Post by: dutch on 16/08/2017 02:17:46
Quote from: Bored chemist on 14/08/2017 20:02:50
Quote from: dutch on 13/08/2017 23:14:17
Please stop embarrassing yourself.
I might not agree with Dutch about many things, but he's spot on with regard to Thebox.
What is embarrassing is adults on a science forum who carry on discussing fairy tales as if fact and reality. Now I know I do not fall into that category because I have a brain in my head.
Do you even know the basics of what's being discussed in this thread?
Quote from: phyti on 14/08/2017 17:09:33
Bored chemist;
I have not seen any tables for td when slow transporting clocks.
Here is one to consider.
https://app.box.com/s/v722vkyrscqo4v5lye0j4nit05gglocy
Thanks, that's the closest anyone has yet got to answering the question I asked several pages ago.
I consider 30m/s (nearly 70MPH) rather fast for a bike.
I also considered continental drift as a possible transport mechanism...
That's for ε = ½. Now prove to me that ε ≠ ¼ etc.
Every single value of ε could be used to make a perfectly viable view of the entire universe (and does not do so for just one reference frame as we can meticulously prove the ENTIRE universe makes sense from any valid foliation/reference frame as is done in SR and GR). ε = ½ for the local frame is merely a CHOICE via convention.
For example:
phyti's equation is L = d/a * ( 1 - γ )
With the above if someone is assuming the gamma affects time it's implied that I ε = ½ for my reference frame and ε ≠ ½ for all other reference frame at least from "my point of view." WHY MUST THIS BE TRUE? Why does the universe give a blank about your "point of view."
Why can't my original reference frame have time dilation AND length contraction? If this is true and I accelerate to velocity v I may have NO length contraction and NO time dilation. Now one would ask: why would it take less time to travel from point A to B if there is no time dilation? Answer: Because the original reference frame is length contracted (by the exact same γ) and it takes less time to traverse the contracted distance when moving at v with no time dilation and when non contracted. The car fitting into the garage paradox in Relativity has more than one mechanism depending on the ε chosen for the frame.
Why would clock B have synchronization to clock A with the assumption ε = ½ even when ε ≠ ½ BECAUSE WE ASSUMED ε = ½ and we have no idea what ε equals. We are free to assume ANY valid convention. We are merely humans and can only know what we can prove in experiment. When infinite valid solutions exist we can't say one must be right.
We know the output t' to the entire Lorentz Equation. We do NOT know parts of it and time dilation is only a PART which includes time dilation, length contraction, changes in simultaneity, and relativistic aberration (the last one when the LT is in its entirety and includes all angles). We do NOT know any of these parts on their own because they are non-local but rather only the whole. t' is the observable output which is symmetric (t' does not equal dilated time). We are perfectly able to apply an ε where the one-way speed of light is NOT c if we wish. Given an infinite number of answers that all make sense it's only convention that we choose to use one of them locally. The choice is not handed down by a God nor does it come from experimental evidence given how Relativity works.
The below explains the twin paradox
https://en.wikipedia.org/wiki/Twin_paradox#/media/File:Rstd4.gif
Quote
In 1913, Henri Poincaré posthumous Last Essays were published and there he had restated his position: "Today some physicists want to adopt a new convention. It is not that they are constrained to do so; they consider this new convention more convenient; that is all.[/b]
Again.........
t'/t = f'/f = (1 - v/c) / γ = γ / (1 + v/c) = (1 - a/c) / (1 + b/c) γb/γa where v = (a + b) / (1 + a b /c²)
τ/t= γb/γa where v = (a + b) / (1 + a b /c²) 0 < τ/t < ∞
The observable output t' is the same for the same v in each form above regardless of a or b. However, the mechanism, length contraction, time dilation, simultaneity, and relativistic aberration are VASTLY different.
Now much of the above is in the context of LET (although all the same math is still used in SR) and one could argue that a block universe (fully 4D universe) does not have "real" length contraction, time dilation etc but only apparent because of rotations in a 4D structure and 3D frames are snapshots of the 4D structure. However, even then how do we know ε = ½? Why not have ε = ¼ for the block? Why couldn't we apply ε = ¼ locally to all reference frames? We definitely can.
Einstein simply chose ε = ½ because it's the easiest convention to use.
one convention's ease of use ≠ other conventions are wrong
Please tell me how a particular convention becomes definite by experimental evidence. If you know how to do this where is your Nobel Prize?
Post by: guest4091 on 16/08/2017 17:16:15
The example you described is shown in the drawing with an arbitrary distance d.
B is moving at an arbitrary speed (.5c) relative to A. Simultaneous signals from the origin (blue) reflect from mirrors M and M'. The red curve shows the standard time unit increasing by γ as a function of speed. The length d is contracted by 1/γ, as a function of speed. The return time at D is equal to 2t.
This is part of the principle of relativity, that an observer in a moving inertial frame may consider themselves at rest, and the description of physical laws (propagation of light) are the same in any inertial frame.
https://app.box.com/s/sx7ir687lkcd89z3uqyiunw52ecv19lk
Post by: guest39538 on 16/08/2017 17:49:29
Quote from: Bored chemist on 14/08/2017 20:02:50
Quote from: dutch on 13/08/2017 23:14:17
Please stop embarrassing yourself.
I might not agree with Dutch about many things, but he's spot on with regard to Thebox.
What is embarrassing is adults on a science forum who carry on discussing fairy tales as if fact and reality. Now I know I do not fall into that category because I have a brain in my head.
Do you even know the basics of what's being discussed in this thread?
Yes indeed, my thread has been high jacked is what is the basics to this thread now. I have already said how to measure the one way speed of light. Time dilation playing no part in my notion.
But never mind, if people can't be bothered to start their own thread, well what can I say.....
Post by: Bored chemist on 16/08/2017 18:43:13
That's for ε = ½. Now prove to me that ε ≠ ¼ etc.What is epsilon?
You haven't explained it.
Also, I have explained exactly what I propose to do in my thought experiment.
Are you saying that the outcome isn't fixed and that if I repeat it I might get a different answer, or that there's some parameter (ε) I have missed.
Well, what is it?
Can I buy some more of it at my local supermarket?
Post by: guest4091 on 17/08/2017 15:10:31
Thanks, that's the closest anyone has yet got to answering the question I asked several pages ago.The limit of td is zero only if you don't move the clocks! To verify your experiment within life expectancy, NASA will (for a fee) place your clocks in space. You can then synch the clocks in a few seconds and be done. Think of the time you'll have for other things.
I consider 30m/s (nearly 70MPH) rather fast for a bike.
I also considered continental drift as a possible transport mechanism..
Post by: guest4091 on 17/08/2017 15:23:34
Quote
Why would clock B have synchronization to clock A with the assumption ε = ½ even when ε ≠ ½ BECAUSE WE ASSUMED ε = ½ and we have no idea what ε equals. We are free to assume ANY valid convention. We are merely humans and can only know what we can prove in experiment. When infinite valid solutions exist we can't say one must be right.
This sounds so familiar! If one is right, the others are wrong. Who said that?
Why the concern of path ratios?
If Einstein is promoting the idea that A can assume a pseudo rest frame, then it's logically consistent that the time out and back are equal, thus his definition.
If A knew his absolute speed in space, he would know the ratio of the light paths out and back, yet he can establish relative simultaneity without knowing it.
An object at absolute rest cannot be found, but we can imagine an absolute rest frame (arf) U for the purpose of showing the differences relative to a moving frame. Einstein then develops the coordinate transformations using c-v and c+v, i.e. light speed relative to a moving object, which can only be observed outside the moving frame.
Expressing events in the moving frames A and B in terms of U events, then allows elimination of U, and expressing B events in terms of A, and the reverse. Neither A nor B have to be an arf, but can serve that purpose if their measured speed of light is c.
The gif link in #141, shows it makes no difference if the light paths are equal or not. The pseudo rest frame is equivalent to an arf.
Post by: dutch on 17/08/2017 18:59:39
This sounds so familiar! If one is right, the others are wrong. Who said that?
The Board Chemist....
Why the concern of path ratios?
Do you mean ε? Isn't that variable the entire point when discussing one-way speeds of light? No one is contesting the two-way speed of light independent of choice of ε so any variance in the one-way speed corresponds to different ε.
If Einstein is promoting the idea that A can assume a pseudo rest frame, then it's logically consistent that the time out and back are equal, thus his definition.
If A knew his absolute speed in space, he would know the ratio of the light paths out and back, yet he can establish relative simultaneity without knowing it.
Please allow me to rewrite this with more accurate language:
If Einstein is promoting the idea that A can (but does NOT have to. remember can ≠ must) assume ε = ½ for their own reference frame, then it's logically consistent that the time out and back are equal under this assumption (which is completely circular but OK), thus his CONVENTION.
If A knew his true value for ε (if such a thing exists), he would know the true one-way speed of light (if such a thing can be absolutely defined), yet even if he doesn't know ε he can use a convention that assumes any ε he pleases.
To prove to me the one-way speed of light is c you must either:
1) Synchronize clocks with an instantaneous light signal.
2) Provide a way to synchronize clocks not based on convention.
You must prove what a "now" is definitively in two spatially separated locations experimentally.
We must have FTL signaling to say anything further on the one-way speed of light (or anything for that matter). We simply form a convention for one-way speeds nothing more.
What is epsilon?
You haven't explained it.
I explained it, I gave an equation for it, I gave links to references discussing it, and I used it multiple times in many posts. I'm not explaining it again so you can just ignore it.
How does anything anyone's written change the answer I originally gave in my first post in this thread?
Post by: Bored chemist on 17/08/2017 19:22:51
"Energy is the capacity to do work" does.
So, the equations don't actually explain epsilon.
Setting that aside for the minute, As I said earlier (and you don't seem to have noticed) I'd really like an answer to my question.
If I did the experiment I proposed,
and then did it again,
one of two things would happen.
I'd get the same answer both times, or I wouldn't.
Which would you expect?
Would the experiment be repeatable?
Post by: David Cooper on 17/08/2017 23:42:54
QuoteWhen infinite valid solutions exist we can't say one must be right.
This sounds so familiar! If one is right, the others are wrong. Who said that?
There aren't infinite valid solutions - there are merely infinite potentially-valid solutions, all of which contradict each other and only one of which can actually be a representation of the actual reality.
Post by: dutch on 18/08/2017 01:13:49
Quote from: phyti on Yesterday at 15:23:34
Quote
When infinite valid solutions exist we can't say one must be right.
This sounds so familiar! If one is right, the others are wrong. Who said that?
There aren't infinite valid solutions - there are merely infinite potentially-valid solutions, all of which contradict each other and only one of which can actually be a representation of the actual reality.
Maybe and I personally would like to think so. However, we can't prove any particular solution correct but we can point out that Einstein Synchronization where ε = ½ for our own frame is an agreed upon choice AKA a convention.
https://en.wikipedia.org/wiki/One-way_speed_of_light There's 49 different sources on this wiki page and I've seen many more.
Quote
The two way speed of light in a vacuum as measured in two (inertial) coordinate systems moving with constant relative velocity is the same regardless of any assumptions regarding the one-way speed.[48][/b]
Even from Einstein's convention ε ≠ ½ for all other frames given ε = ½ for our reference frame from our view. Yet surprisingly (sarcasm)... the laws of physics still work for all frames.
It's not enough for me to accept Einstein Synchronization as anything more than convention unless all other conventions are shown to be invalid. Without having a unique synchronization or instantaneous signaling I'm not about to commit to ANY ε and thus ANY value for the one-way speed of light for any reference frame. I often use Einstein Synchronization simply because it's convenient.
Post by: Bored chemist on 18/08/2017 10:57:47
and then did it again,
one of two things would happen.
I'd get the same answer both times, or I wouldn't.
Which would you expect?
Would the experiment be repeatable?
Post by: guest39538 on 18/08/2017 11:42:29
If I did the experiment I proposed,If your experiment was set up correctly the same as my experiment would need to be, then you should expect repeat results if c is constant that was an identical result every time.
and then did it again,
one of two things would happen.
I'd get the same answer both times, or I wouldn't.
Which would you expect?
Would the experiment be repeatable?
However, the atmosphere is not a vacuum. You need to do it in a vacuum.
Post by: Bored chemist on 18/08/2017 14:28:42
That's a start.If I did the experiment I proposed,If your experiment was set up correctly the same as my experiment would need to be, then you should expect repeat results if c is constant that was an identical result every time.
and then did it again,
one of two things would happen.
I'd get the same answer both times, or I wouldn't.
Which would you expect?
Would the experiment be repeatable?
However, the atmosphere is not a vacuum. You need to do it in a vacuum.
I wonder if Dutch agrees.
If I do the experiment of synchronising two clocks (next to each other) then moving them slowly then using them to time the arrival of a flash of light- with all the details I previously specified.
And then I repeat it.
Will I get the same answer twice?
Post by: guest39538 on 19/08/2017 01:05:14
So, as you say:
The one-way speed oflighteverything: whether it's light, or the number nine bus is simply impossible to measure without applying an arbitrary convention by any known means.
When you fix the problem of t=speed/d to something independent instead, then you can measure the one way speed of anything.
Post by: dutch on 19/08/2017 04:06:24
That's a start.
I wonder if Dutch agrees.
If I do the experiment of synchronising two clocks (next to each other) then moving them slowly then using them to time the arrival of a flash of light- with all the details I previously specified.
And then I repeat it.
Will I get the same answer twice?
Before I answer your question again... let me ask one of my own.
If I have the equation X + Y = A and X and Y could be anything what is X?
The answer you will give based on your history in this thread is X = Y. X and Y could be anything so without extra information this could be correct and maybe it is. Perhaps X always equals Y... perhaps. HOWEVER, there are infinitely many other answers. Without more information we could just make the equation easier by saying X = Y and thus 2X = A but this is just a convention.
Now onto your question:
For the hundredth time you are confusing t' with τ. Watch the math carefully:
I could say t' = γ t = 1/.8 √(1 - .8^2) = .75
Or I could say
t' = ( t - v x ) / γ = (1/.8 - .8 * 1)/√(1 - .8^2) = 2.083333 - 1.3333333 = .75
Wait would you look at that! They're EQUAL.
The time dilation on the first one is γ and the second one is 1/γ. The τ are γ t and t/γ which are NOT the same. The t' IS the same. The two forms above are COMPLETELY different mechanistically.
The entire point of the v x /c² / γ term is to account for frames of different ε which relativity is forced to do (even if they push them to "other" reference frames). Now watch:
½ ( x γ / ( c + v ) - x γ / ( c - v ) ) = ½ x γ * [ (c - v) - (c + v) ] / (c² - v²)
= - ½ x γ 2 v / (c² - v²)
= - v x γ / c² / [ (c² - v²)/c² ]
= - v x / c² / γ (this is the fudge factor or the time added subtracted to a clock to keep it synchronized as viewed
from an ε = ½ frame)
The above gives the EXACT same answer. Let's define ε here as:
ε = t1 / (t2 + t3) = x γ / ( c - v ) / [ x γ / ( c - v ) + x γ / ( c + v ) ]
= 1 / ( c - v ) / [ 1 / ( c - v ) + 1 / ( c + v ) ]
= 1 / ( c - v ) / [ ( c + v ) / (c² - v²) + ( c - v ) / (c² - v²) ]
= 1 / ( c - v ) / [ 2c / (c² - v²) ]
= (c² - v²) / [ 2c (c - v) ]
= ½ c (c² - v²) / [ c² (c - v) ]
= ½ c γ² / ( c - v )
= ½ c² γ² ( c + v ) / [ c ( c² - v² ) ]
= ½ γ² ( c + v ) / [ c γ² ]
= ½ ( 1 + v/c )
This is just ONE formula for ε given a v and there are infinitely many more that can give ANY ε for any v. (generalized equation found in link below)
https://en.wikipedia.org/wiki/One-way_speed_of_light
Why can't I choose another valid ε than ε = ½? Where does my formula for t' fail? If it does not fail then why can't I use it?
Relativity says I CAN always choose ε = ½ for any reference frame locally but it does NOT say I can't choose any other ε. It simply forms a nice convention which greatly streamlines calculations.
The ONLY way I'm going to agree with you is if you prove I MUST choose ε = ½ and all other ε are invalid. Otherwise I must conclude one-way speeds which require a definitive way to synchronize two spatially separated clocks (or send an instantaneous signal) are undefined outside of a convention. "Relative" synchronization via an arbitrary convention is just not good enough.
I ALREADY showed the term -v x / c² / γ and I said it explained how I could choose other ε. I already explained how it depends on x. Considering this term is straight out of the Lorentz Transformation and in both LET and SR you can't deny it's authenticity. You also can't deny that ε ≠ ½ for one of the two frames in the transformation. Nothing stops me from choosing one ε from infinitely many ε.
Considering we do NOT know how to send signals instantaneously and infinitely many planes of simultaneity (foliations in GR) exist and ALL can individually explain the universe we CANNOT know what "now" is in two spatially separated locations. If we don't know what "now" is beyond convention then we don't know one-way speeds (don't forget how I defined v as a two-way average velocity in prior posts).
I also don't care about "slow clock transport" there's a multitude of reasons (many I already gave) on why slow clock transport should be the same as fast clock transport as experiments show. This point you keep trying to make has nothing to do with my freedom to choose ε.
I will never agree with you unless someone gets a Nobel Prize for ending a 110 plus year old debate. I already gave links to all of this and equations. Don't confuse a cute convention with something absolute.
Post by: Bored chemist on 19/08/2017 11:28:39
The answer to this question is "yes" or "no"
If I do the experiment of synchronising two clocks (next to each other) then moving them slowly then using them to time the arrival of a flash of light- with all the details I previously specified.
And then I repeat it.
Will I get the same answer twice?
Post by: dutch on 19/08/2017 13:53:31
Here's a hint.
The answer to this question is "yes" or "no"
If I do the experiment of synchronising two clocks (next to each other) then moving them slowly then using them to time the arrival of a flash of light- with all the details I previously specified.
And then I repeat it.
Will I get the same answer twice?
What is your problem now? I've already given multiple equations for t'. The t' you show doesn't prove what you think.
The question of X + Y = A and we know A does NOT have anything to do with a statement X = Y. You want ε = ½ and I'm saying it could be BUT it does not have to be. You are NOT synchronizing clocks beyond convention because the term - v x / c² / γ tells you that your synchronization is off via the perspective chosen and exactly how much it's off. Other equations for ε also exist and I can assume any ε I wish for any frame I wish. Just because you can choose ε = ½ for your frame does NOT mean you have to. This does not prove Einstein's postulate wrong because a postulate means that you can assume something and always get an answer that works. The postulate does not necessarily mean you can't make other assumptions and scientists have shown you can (and no one has ever shown you can't).
You must be looking at the situation classically where all four relativistic changes (length contraction, time dilation, change in simultaneity, relativistic aberration) do not occur. Repeating your question when I've answered it a dozen times with math and links isn't going to go anywhere for you.
Do you KNOW what happens if an instantaneous signal is sent?
How do you KNOW what a one-way speed is beyond convention if you don't know what happens with an instantaneous signal? We've never experimented with instantaneous signals so we don't know what now is in two different locations. I don't make judgement without experimental evidence. Do you know of any experiment proven to send any information faster than light? If not then you can't provide me anything more than an answer based on convention. What is wrong with the answer "gee we just don't know?"
What is your problem with the statement below?
We can measure the one-way speed of light (or anything) to significant accuracy but only with respect to our choice of convention.
Post by: Bored chemist on 19/08/2017 16:24:08
Well, I have said that if you press the two "reset" buttons on the clocks against one another it is one action and it is local to both clocks and, since it's the same act it is simultaneous with itself for all observers because the alternative would be a violation of causality.
And I have said that , if you have two perfect clocks next to each other, set to "zero" at the same time, they will stay synchronised.
And I have said that, if you move one of them, it will run slow, but if you move it slowly it will not lose much time (and someone kindly provided a table of how slow it would be).
So, since you know how slow it is, you can allow for that.
You keep going on about conventions; well I have tried to define mine.
You keep telling me that the apparent speed depends on epsilon.
I keep asking you if the apparent speed of light I measure will be consistent and, rather than saying yes or no, you keep telling me that instant messaging isn't possible.
Well, I know that- and I never said it was.
So, yet again
If I do the experiment of synchronising two clocks (next to each other) then moving them slowly then using them to time the arrival of a flash of light- with all the details I previously specified.
And then I repeat it.
Will I get the same answer twice?
Post by: dutch on 19/08/2017 17:04:18
You keep going on about conventions; well I have tried to define mine.
So it's a convention. CASE CLOSED my first post stands correct. Good bye.
Post by: guest4091 on 19/08/2017 17:55:25
Quote
Einstein never considered the two way journey of light in his ideas . If he had , he would of known and realised that simultaneity is nothing to do with different now's or different rates of time.
Do more research.
1905 paper, par. 1, 2; A. Einstein:
We have to take into account that all our judgments in which time plays a part are always judgments of simultaneous events.
We have so far defined only an ``A time'' and a ``B time.'' We have not defined a common ``time'' for A and B, for the latter cannot be defined at all unless we establish by definition that the ``time'' required by light to travel from A to B equals the ``time'' it requires to travel from B to A.
So we see that we cannot attach any absolute signification to the concept of simultaneity, but that two events which, viewed from a system of co-ordinates, are simultaneous, can no longer be looked upon as simultaneous events when envisaged from a system which is in motion relatively to that system.
Post by: guest39538 on 19/08/2017 17:57:10
I have never claimed that an instant signal is sent.You can simply put your reset button of the two clocks exactly in the middle, the time it takes the signal to travel to both clocks will be synchronous if the wires are the same length from each clock. , this will allow both of your clocks to start ''counting'' time , synchronous.
Well, I have said that if you press the two "reset" buttons on the clocks against one another it is one action and it is local to both clocks and, since it's the same act it is simultaneous with itself for all observers because the alternative would be a violation of causality.
And I have said that , if you have two perfect clocks next to each other, set to "zero" at the same time, they will stay synchronised.
And I have said that, if you move one of them, it will run slow, but if you move it slowly it will not lose much time (and someone kindly provided a table of how slow it would be).
So, since you know how slow it is, you can allow for that.
You keep going on about conventions; well I have tried to define mine.
You keep telling me that the apparent speed depends on epsilon.
I keep asking you if the apparent speed of light I measure will be consistent and, rather than saying yes or no, you keep telling me that instant messaging isn't possible.
Well, I know that- and I never said it was.
So, yet again
If I do the experiment of synchronising two clocks (next to each other) then moving them slowly then using them to time the arrival of a flash of light- with all the details I previously specified.
And then I repeat it.
Will I get the same answer twice?
However you don't need a clock to time the one way speed of light. You need a strobe set to one flash per second. You then need a detector distance x apart and the detector read out speed to be 5cm a second.
This will firstly test that c is c.
dx=dy
ok?
Post by: guest39538 on 19/08/2017 18:02:57
The box #121;And he is talking about sight, think about it.QuoteEinstein never considered the two way journey of light in his ideas . If he had , he would of known and realised that simultaneity is nothing to do with different now's or different rates of time.
Do more research.
1905 paper, par. 1, 2; A. Einstein:
We have to take into account that all our judgments in which time plays a part are always judgments of simultaneous events.
We have so far defined only an ``A time'' and a ``B time.'' We have not defined a common ``time'' for A and B, for the latter cannot be defined at all unless we establish by definition that the ``time'' required by light to travel from A to B equals the ``time'' it requires to travel from B to A.
So we see that we cannot attach any absolute signification to the concept of simultaneity, but that two events which, viewed from a system of co-ordinates, are simultaneous, can no longer be looked upon as simultaneous events when envisaged from a system which is in motion relatively to that system.
Imagine you are on Earth and I will be on Saturn and we are both observing the Sun, we are both seeing the Sun at different times due to the nature of how sight/light works.
However your next increment of time is immediately ahead of you, the same as mine, our times are synchronous and remain synchronous although we see things at different times.
That would be the conventional understanding of simultaneity of events. However , when we look at the vector analysis of the light involved, we see each other synchronously as well.
Δt=tP adds absolute significant
vector analysis of light between two observers using the distance of L=299 792 458m
Vector
=v+(c)1.sVector
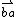=v-(c)1.snet difference t = 0t
net difference.jpg (22.3 kB . 1015x625 - viewed 4588 times)Because X amount of time Planks = 1.s = 299 792 458m
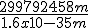=1.855e+43 tP's / secondAll observers anywhere in the Universe experience 1.855e+43 tP's/second because c is constant. My clock is very accurate.
In time dilation theory and the Lorentz length contraction, this is not accounted for, the shorter slower time being exactly that, a short measurement that has not travelled 1.855e+43 tP's/second .
Post by: Bored chemist on 19/08/2017 20:41:08
You can simply put your reset button of the two clocks exactly in the middle, the time it takes the signal to travel to both clocks will be synchronous if the wires are the same length from each clock. , this will allow both of your clocks to start ''counting'' time , synchronous.No.
However you don't need a clock to time the one way speed of light. You need a strobe set to one flash per second. You then need a detector distance x apart and the detector read out speed to be 5cm a second.
This will firstly test that c is c.
dx=dy
ok?
Sorry, but it's not OK.
You can't synchronise two clocks unless they are in (essentially) the same place.
And the rest makes no real sense.
Post by: Bored chemist on 19/08/2017 20:43:37
ByeYou keep going on about conventions; well I have tried to define mine.
So it's a convention. CASE CLOSED my first post stands correct. Good bye.
Pity you didn't have time to answer my question before you went.
Post by: guest39538 on 19/08/2017 22:24:55
Huh? you suggested the reset button to synchronise the clocks, I just told you too put your reset button an equal length apart from each clock, i.e in the middle.You can simply put your reset button of the two clocks exactly in the middle, the time it takes the signal to travel to both clocks will be synchronous if the wires are the same length from each clock. , this will allow both of your clocks to start ''counting'' time , synchronous.No.
However you don't need a clock to time the one way speed of light. You need a strobe set to one flash per second. You then need a detector distance x apart and the detector read out speed to be 5cm a second.
This will firstly test that c is c.
dx=dy
ok?
Sorry, but it's not OK.
You can't synchronise two clocks unless they are in (essentially) the same place.
And the rest makes no real sense.
Added - I tell you what my friend lol, you can use the clock I am using if you want to , a Planck light clock.
Δt=
=cI think you will find it very accurate and constant in any inertia frame of reference or in motion.
You can use the value 1.855e+43 tP's = 1 second
Post by: Bored chemist on 20/08/2017 19:25:23
If you are stood next to one clock a and you see the other as reading the same time , you might say they are synchronised.
But if you go to the other and look back you will say that they no longer agree.
Synchrony only exists locally.
Post by: guest39538 on 20/08/2017 23:29:00
The clocks have to be in the same place in order for "synchronisation" to make sense.Only if you are using a crap clock such as the caesium atomic clock. It is the clock that is faulty not the synchronisation of time.
If you are stood next to one clock a and you see the other as reading the same time , you might say they are synchronised.
But if you go to the other and look back you will say that they no longer agree.
Synchrony only exists locally.
You quite clearly ignore my notions , but if you accepted my notions and used the Planck light clock, then you would not have a problem of synchronising clocks to worry about .
Post by: David Cooper on 21/08/2017 00:08:53
Pity you didn't have time to answer my question before you went.
The answer is that if you repeat your experiment, you'll get the same result, and if the whole system has accelerated in between the original experiment and the repeat, you'll still get the same result. You will think you've kept the clocks in sync each time regardless of whether they are really still in sync or not.
Post by: guest4091 on 21/08/2017 16:52:07
And he is talking about sight, think about it.Most of our sensory input is via sight, and he surely thought about it. If you don't understand the theory, just say so. We are all ignorant of something.
Post by: guest4091 on 21/08/2017 17:05:57
The clocks have to be in the same place in order for "synchronisation" to make sense.Einstein described the clock synch method since there was no universal time,or common time for A and B. The idea is not to see the other clock indicate the same as the one next to you, but after the distant clock signal arrives, you deduct the transit time, and conclude the distant clock was indicating the same time when/while/simultaneusly you were viewing the one next to you.
If you are stood next to one clock a and you see the other as reading the same time , you might say they are synchronised.
But if you go to the other and look back you will say that they no longer agree.
Synchrony only exists locally.
The synch convention does not require adjacent clocks. That's why you use light signals. Yes the simultaneity is local, since it depends on the speed of the frame.
Post by: guest39538 on 22/08/2017 15:38:32
What is to understand?And he is talking about sight, think about it.Most of our sensory input is via sight, and he surely thought about it. If you don't understand the theory, just say so. We are all ignorant of something.
Let us look at the Wiki explanation.
Quote
According to the special theory of relativity, it is impossible to say in an absolute sense that two distinct events occur at the same time if those events are separated in space. For example, a car crash in London and another in New York, which appear to happen at the same time to an observer on Earth, will appear to have occurred at slightly different times to an observer on an airplane flying between London and New York. The question of whether the events are simultaneous is relative: in the stationary Earth reference frame the two collisions may happen at the same time but in other frames (in a different state of motion relative to the events) the crash in London may occur first, and in still other frames the New York crash may occur first. However, if the two events could be causally connected (i.e. the time between event A and event B is greater than the distance between them divided by the speed of light), the order is preserved (i.e., "event A precedes event B") in all frames of reference.
Of course I am clueless. Relative to C and D the event is absolute where relative to A and B the event happened at different times,
L(xy)≠L(x)
L(yx)≠L(x)
clueless.jpg (37.1 kB . 1015x625 - viewed 4404 times)No idea me .....
v-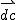
=v+
≠v-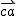
p.s of course when I look at the truth of this and consider my own notions on the nature of light, the notions fail and the reference frame is always absolute to the observer. I.e simultaneously .
My model rubs out the lines between events, the only change we observe is of the body itself in its exact location.
transparent.jpg (21.21 kB . 1015x625 - viewed 4426 times)Because light and dark only exists of bodies. I observe the entire length of space between my eye and object. I observe the objects colour in its exact geometrical position relative to me, I can measure this , I can move towards the object and the object will occupy my present, I can move away from the object the object is my past geometrical position but remains in my present always , I can go back to the object to prove this over and over again .
Time can not slow down if I return to the present or the object returns to my present, I do not see objects in the past I see them in the present a distance away, an entire distance we can as a part of the whole we can see, we observe the entire universe simultaneously.
However I can not force anybody to believe this although I am being totally objective to what I observe. I observe visible light to be only that of substance, the same as dark and light is only that of substance, the reality is that all bodies are existing in absolute nothingness , absolute nothingness is where time , light or dark do not exist without physical substance.
https://en.wikipedia.org/wiki/Relativity_of_simultaneity
And as far the Lorentz contractions I have also shown that to be false in my diagrams in my paper using tP (time Planck).
In the beginning there was absolute nothingness 0∞, where time , light and dark did not exist.
Post by: Bored chemist on 22/08/2017 18:37:13
The thing about, for example, a caesium clock, is that it tells the time.The clocks have to be in the same place in order for "synchronisation" to make sense.Only if you are using a crap clock such as the caesium atomic clock. It is the clock that is faulty not the synchronisation of time.
If you are stood next to one clock a and you see the other as reading the same time , you might say they are synchronised.
But if you go to the other and look back you will say that they no longer agree.
Synchrony only exists locally.
You quite clearly ignore my notions , but if you accepted my notions and used the Planck light clock, then you would not have a problem of synchronising clocks to worry about .
If your "clock" doesn't agree with it then it isn't really a clock.
Post by: Bored chemist on 22/08/2017 18:40:07
I did specify that gravity was the same throughout the experimental arena.Pity you didn't have time to answer my question before you went.
The answer is that if you repeat your experiment, you'll get the same result, and if the whole system has accelerated in between the original experiment and the repeat, you'll still get the same result. You will think you've kept the clocks in sync each time regardless of whether they are really still in sync or not.
Since you can't distinguish gravity from an acceleration...
If I was accelerating I'd know about it (in principle).
I'm not.
So, I should get the same answer each time.
Right?
Post by: David Cooper on 22/08/2017 20:40:41
If I was accelerating I'd know about it (in principle).
I'm not.
So, I should get the same answer each time.
Right?
Yes, you'll get the same answer each time. My point was that even if you accelerate in between, you'll still get the same answer, unless you try to account for the acceleration, at which point you could base things on the original frame of reference in which you were at rest and determine that the second measurement gives you a speed of light relative to the clocks that isn't c, or alternatively you might reassess your first measurement on the basis that you're now at rest, in which case you'll decide that your first measurement gave you a value different from c.
Post by: guest39538 on 22/08/2017 22:25:09
The thing about, for example, a caesium clock, is that it tells the time.The clocks have to be in the same place in order for "synchronisation" to make sense.Only if you are using a crap clock such as the caesium atomic clock. It is the clock that is faulty not the synchronisation of time.
If you are stood next to one clock a and you see the other as reading the same time , you might say they are synchronised.
But if you go to the other and look back you will say that they no longer agree.
Synchrony only exists locally.
You quite clearly ignore my notions , but if you accepted my notions and used the Planck light clock, then you would not have a problem of synchronising clocks to worry about .
If your "clock" doesn't agree with it then it isn't really a clock.
How absurd, the Caesium atom is no more than a measuring tool , we count the amount of cycles to equal 1 second of time passed. The Caesium does not tell the time period.
Quite clearly you have no response to my axiom notions and are clutching at straws with false beliefs. Like it or not I am correct about time.
Post by: guest4091 on 23/08/2017 17:37:12
My point was that even if you accelerate in between, you'll still get the same answer,SR clock synch is relative to the frame speed. If the frame increases speed, the clocks will be out of synch.
Post by: Bored chemist on 23/08/2017 18:34:27
Well, that's nice.If I was accelerating I'd know about it (in principle).
I'm not.
So, I should get the same answer each time.
Right?
Yes, you'll get the same answer each time. My point was that even if you accelerate in between, you'll still get the same answer, unless you try to account for the acceleration, at which point you could base things on the original frame of reference in which you were at rest and determine that the second measurement gives you a speed of light relative to the clocks that isn't c, or alternatively you might reassess your first measurement on the basis that you're now at rest, in which case you'll decide that your first measurement gave you a value different from c.
It means that, whatever epsilon may be, it doesn't matter.
For the moment, I'm leaving out other complications like a passing spaceman or nearby black holes.
Post by: David Cooper on 23/08/2017 20:50:31
My point was that even if you accelerate in between, you'll still get the same answer,SR clock synch is relative to the frame speed. If the frame increases speed, the clocks will be out of synch.
If you do the experiment, then accelerate, then do the experiment again, clearly doing the experiment again involves reuniting the clocks and making sure they're in sync before separating them again.
____________________________________________________________________
Well, that's nice.
It means that, whatever epsilon may be, it doesn't matter.
It does matter, because whenever you do your experiment, you are using epsilon=1/2 without realising it.
Post by: Bored chemist on 23/08/2017 21:04:56
Is that the same value they use for measuring the speed of Usain Bolt?My point was that even if you accelerate in between, you'll still get the same answer,SR clock synch is relative to the frame speed. If the frame increases speed, the clocks will be out of synch.
If you do the experiment, then accelerate, then do the experiment again, clearly doing the experiment again involves reuniting the clocks and making sure they're in sync before separating them again.
____________________________________________________________________Well, that's nice.
It means that, whatever epsilon may be, it doesn't matter.
It does matter, because whenever you do your experiment, you are using epsilon=1/2 without realising it.
Post by: guest4091 on 24/08/2017 15:44:56
If you do the experiment, then accelerate, then do the experiment again, clearly doing the experiment again involves reuniting the clocks and making sure they're in sync before separating them again.For some strange reason, I misread his original description. Mind must be wandering!
Post by: guest4091 on 24/08/2017 15:49:08
In the A-frame, the right drawing, the round trip time is the same, whether the relative speeds c±v or c is used. The only uncertainty is time of reflection, R2 or (R2). This can not be verified if there is no absolute speed for the A-frame. The speed in the example is only the perception of the U-frame, and would be different for other frames of reference. Motion is relative to a reference object, and only has meaning in that sense.
Where the SR convention presents a problem, is composition of velocities
.https://app.box.com/s/c4zwx1aym3oi6924y0dzojkjwyf5z66q
Post by: David Cooper on 24/08/2017 21:02:36
Is that the same value they use for measuring the speed of Usain Bolt?
Yes - they measure his speed relative to the track, and, thanks to the maths of relativity, it doesn't matter how fast the track is moving. If we can ever find a way to identify the absolute frame though, all records for absolute speed might have to be set in the same week or even day of the year on the equator at altitude, but run a 100m race in the wrong direction and the crowd will be faster than the athletes while sitting down.
Post by: GoC on 25/08/2017 13:31:04
Just like there is no preferred frame there is different values for the measurement's of Planck's length for a frame. Plank's length is related to Planck's time in every frame.
Post by: guest39538 on 26/08/2017 13:53:27
TheboxHuh ? planck time is the time it takes light to travel a plank length , however I am not timing it , the light travelling the length is my time I am using.
Just like there is no preferred frame there is different values for the measurement's of Planck's length for a frame. Plank's length is related to Planck's time in every frame.
Post by: guest39538 on 26/08/2017 13:57:14
Is that the same value they use for measuring the speed of Usain Bolt?
Yes - they measure his speed relative to the track, and, thanks to the maths of relativity, it doesn't matter how fast the track is moving. If we can ever find a way to identify the absolute frame though,
All speed is absolute to the absolute reference frame I have already explained before but nobody listens. Never mind I am out of here, sick of talking to the wall now , death ears.. I think science is a branch of religion, that is the only thing that makes any sense to why science does not want to listen to me. I kill God and they don't like that to much.
Post by: guest4091 on 26/08/2017 18:50:33
Is that the same value they use for measuring the speed of Usain Bolt?It's the only value you would use for a rest frame. There is no reason light speed would vary over the same course if space is uniform in density.
Recalling the train experiment, you toss an object across the aisle to someone opposite you, and they catch it. You don't need to know the train is moving since all objects in the train have the trains velocity. If it is added, it can easily be subtracted.
I.e. any experiment in any inertial frame is independent of what the universe is doing outside that frame.
Post by: GoC on 01/09/2017 11:49:22
The relative physical laws are the same in every inertial frame but the conditions of the different inertial frames are not. The relative energy we measure as time is affected with an increase in velocity. So reaction times differ like your synapsis not firing as fast in greater inertial speed. In this way you do not recognize any difference in reaction rates. Timing changes with your synapsis so the conditions remain the same physical laws relative.
Post by: The Spoon on 01/09/2017 13:28:01
Death ears! Brilliant. Where can I buy some?Is that the same value they use for measuring the speed of Usain Bolt?
Yes - they measure his speed relative to the track, and, thanks to the maths of relativity, it doesn't matter how fast the track is moving. If we can ever find a way to identify the absolute frame though,
All speed is absolute to the absolute reference frame I have already explained before but nobody listens. Never mind I am out of here, sick of talking to the wall now , death ears.. I think science is a branch of religion, that is the only thing that makes any sense to why science does not want to listen to me. I kill God and they don't like that to much.
Post by: guest39538 on 01/09/2017 14:30:58
Death ears! Brilliant. Where can I buy some?Is that the same value they use for measuring the speed of Usain Bolt?
Yes - they measure his speed relative to the track, and, thanks to the maths of relativity, it doesn't matter how fast the track is moving. If we can ever find a way to identify the absolute frame though,
All speed is absolute to the absolute reference frame I have already explained before but nobody listens. Never mind I am out of here, sick of talking to the wall now , death ears.. I think science is a branch of religion, that is the only thing that makes any sense to why science does not want to listen to me. I kill God and they don't like that to much.
Whoops! I did it again
Sorry I meant deaf, I type as I am thinking it, a sort of ''live'' feed to my thoughts, that is why sometimes it is a bit ''gargled''.
Post by: The Spoon on 01/09/2017 15:32:11
English must be very confusing when it is obviously not your first language! Hence the hilarious use of 'gargled' instead of garbled!Death ears! Brilliant. Where can I buy some?Is that the same value they use for measuring the speed of Usain Bolt?
Yes - they measure his speed relative to the track, and, thanks to the maths of relativity, it doesn't matter how fast the track is moving. If we can ever find a way to identify the absolute frame though,
All speed is absolute to the absolute reference frame I have already explained before but nobody listens. Never mind I am out of here, sick of talking to the wall now , death ears.. I think science is a branch of religion, that is the only thing that makes any sense to why science does not want to listen to me. I kill God and they don't like that to much.
Whoops! I did it again
Sorry I meant deaf, I type as I am thinking it, a sort of ''live'' feed to my thoughts, that is why sometimes it is a bit ''gargled''.
Post by: guest39538 on 01/09/2017 16:55:13
I kind of think that at times the readers are reading my posts as if I am gargling out the words, mumbling my sentences. This is because at times I am not focused on what I am writing, I am focused on the thought and ''jotting'' it down .English must be very confusing when it is obviously not your first language! Hence the hilarious use of 'gargled' instead of garbled!Death ears! Brilliant. Where can I buy some?Is that the same value they use for measuring the speed of Usain Bolt?
Yes - they measure his speed relative to the track, and, thanks to the maths of relativity, it doesn't matter how fast the track is moving. If we can ever find a way to identify the absolute frame though,
All speed is absolute to the absolute reference frame I have already explained before but nobody listens. Never mind I am out of here, sick of talking to the wall now , death ears.. I think science is a branch of religion, that is the only thing that makes any sense to why science does not want to listen to me. I kill God and they don't like that to much.
Whoops! I did it again
Sorry I meant deaf, I type as I am thinking it, a sort of ''live'' feed to my thoughts, that is why sometimes it is a bit ''gargled''.
The problem is though, my brain seems endless in thoughts. However the way I write things, does not really affect the ideas. I do explain a lot better these days .
Post by: xersanozgen on 21/07/2020 15:24:16
1- White box is a remote control unit buttons. Connections are obtained with cables (lengths must be equal).
2- Led/light markers are on the monitors of atomic clocks.
3- Atomic clocks are on the same altitude and temperature and isolated from magnetism. (It can be used the corner points of a stadium)
4- Button 1 begins the video cameras.
5- Button 2 shots led/light markers.
6- Button 3 ends the experiment.
7- The moments T i are read on video films for first or last moments of light markers.
8- The difference of syncronisation can be interpreted.
9- The image of left clock on right top camera is the moment Tı and the image of right clock on right lower camera is the moment T2.
10- İnverse readings are for confirmation.
Note top cameras are televideocameras (e.g. 150x - 500x).
My experiment solves all problems.
The atomic clocks are placed on the corners of a stadium ( L = 100 meters).
led markers flash at a same moment due to cables (their lengths are equal).
Even if the atomic clocks are not syncronized, left and right videos provide correcting possibility.
The theoretical essence of this experiment (https://vixra.org/abs/2006.0224) allows to detect the expanding speed of universe; thereby a person who performed this exp. may be candidate for NOBEL prize.