Post by: Dubbelosix on 27/08/2017 16:55:09
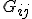is symmetric - I tried to argue a proportionality of terms from the tensor - but we must keep in mind what Matti has said because it is important to remember.The commutation relationship is (in a usual convention)
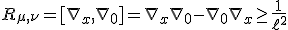
Here we have explicitly wrote out the connections as having commutative properties satisfying our desired inequality. Writing the whole commutation out to find the christoffel symbols, (using differential notation) reveals the following and using general indices:
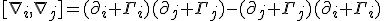
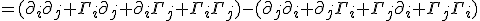
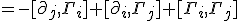
Pulling it out of its differential notation form, what we really have is
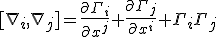
It is one that follows the spacetime relationship
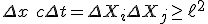
An application of the commutator can be found from parallel transport, in which one can obtain the identity
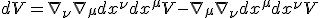
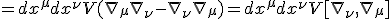
Consider now, the Riemann tensor with torsion. It is basically a commutator acting on some vector field
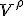
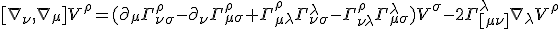
The full Reimann tensor is
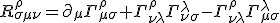
The last two terms in
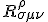display antisymmetry in the commutators. Again the commutation arises from the derivatives of the connections,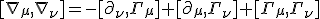
This was the exact identity of the two commutators for derivatives concerned in space and derivatives in time - it's much more simple in the construct than the full Riemann tensor would suggest. The Riemann tensor vanishes, if we are in any coordinate system
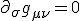
Then the Christoffel symbols are zero
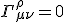
and
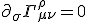
and so
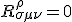
Clearly, we are looking into cases though in which
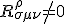
In which curvature does not vanish, but has a specific meaning and relationship with spacetime.
So far, what we have learned, it is the last two terms in Riemann tensor is antisymmetric:
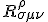. We want to deal in spaces, maybe even two dimensional cases that are not locally Euclidean - ie. a vanishing Riemann tensor concerned with a commutation between connections describing the space and time derivatives. Hopefully we have clarified any misunderstanding of the commutators role in this and how they are interpreted as an anti-symmetric part of the Riemann tensor. I will continue the work with new ideas later.
Post by: Dubbelosix on 27/08/2017 23:42:11
Spacetime non-commutativity is defined by replacing the canonical variables with commutation relationships - it seems also non-trivial that the connections of the gravitation field in question have dimension of
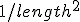and so, it seems very natural to assume maybe gravity will follow the same dynamics on the Planck scale. This application of uncertainty into the equations requires a full interpretation. The preliminary investigation which leads to this idea of some unification between gravity and the quantum structure of spacetime came from an investigation into a quantum interpretation of the Geon particle. This required an interpetation where the geometry could be larger than a specified wavelength imposed by the spacetime uncertainty. These uncertainties in spacetime, which is just a reinterpretation of the usual uncertainty principle between energy and time, can be thought of as corrections on a manifold that are deviating it from the classical world. Using this understanding, nothing seems more natural than to look for such non-trivial spacetime relationships and see how they would (directly) relate to gravity - if they can. This may be a key point of how we may be thinking about it wrongly; as Susskind suggested, 
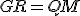though it has been suggested not to be taken as a literal equality, there may already be cases which hint that gravity already has commutation possibilities to describe why these corrections are imposed at a Planck length.We know what that relationship is, we defined it as taking the form of an antisymmetric tensor
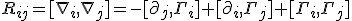
How do we interpret this, without delving into the mathematics too deep this time around?
One interpretation may come from Von Neumann actually suggested that a point in quantum phase space is meaningless because of the uncertainty principle - there may be undertones or preferrably, direct relationships of this with regards to relativity. In a way, general relativity already had concluded from base concepts that points in themselves, are not actually physical. General relativity found a solution by treating not only the interaction of a system but also their worldlines. Notice though, in the Von Neumann universe, this becomes a non-problem, because points in space themselves are simply not physical systems when you appropriately correct them using the commutation.
We can intrepret maybe further, as you converge into the quantum Planck scales, you diverge from the classical theory and must be described by the corrected theory, which does involve a concept of the non-commutation. There are other things we must remain vigilant about such theories: Such as any possible unitary violations that can be understood simply as
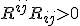
After some reading, I found an author https://arxiv.org/pdf/hep-th/0007181v2.pdf who has applied the uncertainty identical to me, but hasn't looked at the theory from the same perspective. They find for the equality term ~
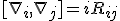
And they identify
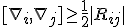
Which is a very useful construction to remember. Eventually I might find an author who has investigated it directly as I have. My idea was based on dimensional grounds only, so we investigated likely only one small corner of this field.
Post by: Dubbelosix on 30/08/2017 13:14:06
It is well known from Pythagoras' theorem that there exists the spacetime inequality ~
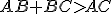
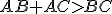
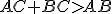
Is it possible to apply a spacetime commutator inside of this inequality? Yes I think so! Or at least, this occurred to me.
For a scalar product defind on a vector space the length of vector is determined by
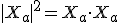
With some invesigation (see references) a spacetime inequality can indeed satisfy the following relationship
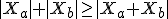
Squaring both sides also yields
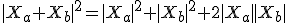
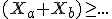
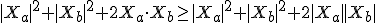
from which it follows
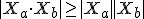
which is known as the Cauchy Schwartz inequality which can be thought of as a direct interpretation of a spacetime uncertainty. Another important identity whicch further can be identified from the spacetime relationships is
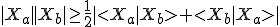
If you have trained your eye on all my previous work into gravity, this looks like the structure of commutators!
In a Hilbert space, you can define new vectors
\sqrt{| < \Delta X_A^2 > < \Delta X_B^2>|} \geq \frac{1}{2} i < \psi |X_A X_B| \psi > + i < \psi |X_B X_A| \psi > = \frac{1}{2} < \psi |[X_A, X_B]| \psi >
(system here can't deal with the latex ^^^ translate it for yourself if you can in code
The left hand side calculates the deviation of the derivative from the mean of the derivative, at least, that is how it would be interpreted in the approach we took to the quantization of gravity. We will use these solutions as a benchmark into how to treat this commutivity in spacetime from the connections we solved.
ref http://rocs.hu-berlin.de/qm1415/resources/Lecture_Notes_10_11_12.pdf
Post by: Dubbelosix on 30/08/2017 13:55:51
To give a hint in how to do this unification attempt, we have three key equations,
1.
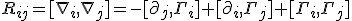
These are the exact Christoffel symbols of the antisymmetric tensor indices
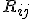.2.
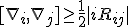
This was an equation derived by another author, finding the relationship in a different form argued from quantum mechanics. As you will see in key equation 3. the form has similarities to application of a Hilbert space ~
3.
\sqrt{|<\Delta X_A^2>< \Delta X_B^2>|} \geq \frac{1}{2} i(< \psi|X_AX_B|\psi > + <\psi|X_BX_A|\psi>) = \frac{1}{2} <\psi|[X_A,X_B]|\psi>
Again, this is a Hilbert spacetime commutation relationship of operators which has to translate into the gravitational dynamics dictated by key equation 1.
So let's put it altogether, its just like a jigsaw puzzle now. Implemented the Christoffel symbols in approach 1. into approach 2. we get
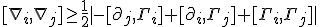
In the framework of the Hilbert space it becomes - assuming everything has been done correct, takes the appearance of ~
\sqrt{|<\nabla_i^2>< \nabla_j^2>|} \geq = \frac{1}{2} i(< \psi|\nabla_i\nabla_j|\psi > + <\psi|\nabla_j\nabla_i|\psi>) = \frac{1}{2} <\psi|[\nabla_i,\nabla_j]|\psi> = \frac{1}{2} <\psi | R_{ij}| \psi > = \frac{1}{2} < \psi |- [\partial_j, \Gamma_i] + [\partial_i, \Gamma_j] + [\Gamma_i, \Gamma_j]| \psi >
without imaginary number on
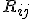
Post by: Dubbelosix on 05/09/2017 17:39:11
Since we used an antisymmetric object identical to the antisymmetric indices of a Reimann tensor, the Riemann tensor will still be symmetric under an interchange of its first two indices with its last two. We have argued that the Riemann tensor
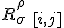where we use a notation to denote the antisymmetric part 
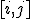. In a valid approach, we have also assumed dynamics satisfying: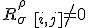
Bianci idenities are to be studied now - they are related to the vanishing of a Reimann tensor in the sense it is related to the vanishing of the covariant derivative - the quantum Bianchi identity is to assume there is a quantum, non-zero interpretation of the commutation of two the two connections,
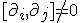
In general relativity, this relationship is usually given as zero - its not difficult to understand, why if we are talking about quantum deviation from a classical theory, why a non-zero theory may be important.
We can argue (maybe) that only points are unphysical and lead to the vanishing of the derivatives
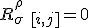, or even only for classical theory, or both. Of course, the statement''if it is true in one coordinate system it must be true in any coordinate system,''
Is hard to argue with - but there is more to play with here than just coordinates - by assuming a spacetime relationship at quantum scales by satisfying the spacetime noncommutativity - so scale is an important factor here when talking about gravity, and the spacetime uncertainty needs to be a phenomenon regardless of the coordinate of the system! When we think about Von Neumann operators and phase space, we expect a deviation from the classical way of thinking anyway...
The spacetime relationship
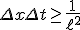
is a model of discretized spacetime - leading to a Planckian spacetime dynamic. The non-zero value of the derivatives implies we have a description of gravity at a quantum scale related to fundamentally to the structure of space. The vanishing of the Riemann tensor is actually related to the same idea connected to the contraction of the Bianchi identities, which are only zero if they permit a symmetric theory of gravity.
If we think about the vanishing of a metric in terms of the vanishing of an action, the action vanishes because it is invariant under general coordinate transformations - that is, general covariance means there is an invariance of the form of physical laws under any arbitrary differentiable coordinate transformations. But I note again, coordinates in a quantum domain to coordinates in the classical domain, may not change the coordinate but definitely the situation. - notably positions are affected by momentum in phase spaces - something classical space time and the classical objects inside of it are so different.
Post by: Dubbelosix on 05/09/2017 19:21:06
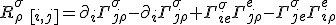
The curvature and torsion is given by
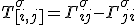
When torsion is non-zero, the Riemann tensor becomes a matrix/object describing the torsion. Though torsion remains a possible way to create a non-vanishing theory of the Riemann curvature, I still prefer a new ''look'' on how we view things - that ''new look'' on things was an argument that quantum domains and classical domains yields different understanding of the physics.... though the statement, ''the laws of physics are true in every coordinate frame'', is correct, I don't dispute this, but the idea that this should transcend into phase space with the same value is hypothesis. In fact, we argue there is a non-vanishing structure to spacetime itself!
For particles that do not have radii, (point particles) we can argue something happens in two ways:
1) Relativity implies as R decreases, the curvature increases and as it approaches zero, approaches infinity: Whether or not a point actually implies infinite curvature is for philosophers, for me, it just implies a non-physical situation. A singularity. You can also argue that self-energies become divergent as well.
2) If on the other hand, we are led to believe that electron particles are not actually pointlike, then this avoids infinite curvature and infinite energy and we save a definition of the electron which must have a radius-structure and therefore a curvature R and a stress energy T and a non-vanishing curvature in Riemann geometry.
Post by: Dubbelosix on 06/09/2017 02:32:43
The first term doesnt matter, the indice can be covariant or contravariant. The identity satisfies sign changes in the order of the last three indices
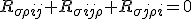
To create the first Bianchi term is easy, contract a definition of the curvature with the metric tensor
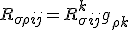
Using the same principles, you can form the other three, now all three are, assuming I have done this right
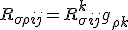
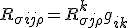
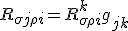
There is a commutation relationship it seems between the metric and the connections. Using the formulation above though, we can see an equivalent form then of the Bianchi identity is
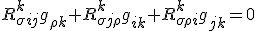
Or simply as
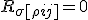
In which the bracket denotes the antisymmetric part of the tensor, which arises from the antisymmetry in
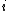and 
and 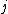the definition of 
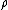is entangled into it.
Post by: Dubbelosix on 06/09/2017 03:30:47
It's also nice to note, this last identity can be seen to be related to the Jacobi triple vector product
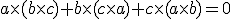
In which case, we understand it from the following relationship using basis vectors:
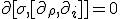
Post by: Dubbelosix on 06/09/2017 04:05:06
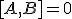you will know this by now as the commutation relation.Classical it will be zero, but quantum mechanics tells a different story in which the difference is measured by
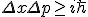
This shows there are no quantum observables corresponding to the action. Understanding why though this means we have entered the quantum realm is unclear. Even in modern references I have looked for.
Usually when you see something like
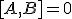
It can also be taken as a statement of conservation. Clearly
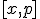does not equal zero in the quantum domain and the presence of the quantization 
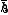is not an indication of a breakdown of any conservation law. Isn't it interesting though, we have been speaking about the non-commutation between space and time - this suggests three possible uncertainty relationships with time by using the three space dimensions.
However, in quantum mechanics, objecfs like commutators are made up of observables. Does this expose a flaw in the understanding of the physics, since time is not an observable? Time doesn't even have a non-trivial operator. So how can time be seen as or like an observable, in some phase space, when it isn't?
This is a good question and I may not have the best of answers, - only than to say, we need to remember, while it seems natural to call it a spacetime uncertainty relationship, its actually just a reinterpretation of the usual energy time relationship.
So while it may seem like we are forced to deal with an object which isn't an observable, technically-speaking, its about the energy-time relationship and the large uncertainties in the momentum of scattered paricles implies that the number of particle states in the short distance of region satisfies
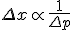
So this is not a true modification but is rather an interpretation, according to Yoneya.
Post by: Dubbelosix on 06/09/2017 19:18:48
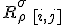
which has been well-established now it has antisymmetric indices. It also has to be true that the following commutation properties hold
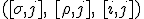
That is the time deriative anti-commutes with the rest of the space derivatives.
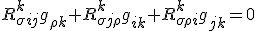
Is a form of the Bianchi identity. It may be a good question to ask, whether the first and last Riemann terms have commutation between the metric term at the end. We'll work that out in time. We seem to have ''partially'' created a quantum Bianchi identity by understanding the commutation written in the form
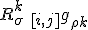
So question is, what notation do we use to express commutation on the first and last cyclic Riemann terms? This serves as a lead forward.
Post by: jeffreyH on 06/09/2017 20:59:56
http://mathworld.wolfram.com/ChristoffelSymboloftheSecondKind.html
Post by: Dubbelosix on 06/09/2017 22:09:56
Those darn symbols and their affine connections!
http://mathworld.wolfram.com/ChristoffelSymboloftheSecondKind.html
Indeed, I just checked back as well and found two wrong indices, in wrong places! best to check everything.
Post by: Dubbelosix on 06/09/2017 23:02:10
The first term is the first cyclic form of the Riemann tensor is
which has been well-established now it has antisymmetric indices. It also has to be true that the following commutation properties hold
That is the time deriative anti-commutes with the rest of the space derivatives.
Is a form of the Bianchi identity. It may be a good question to ask, whether the first and last Riemann terms have commutation between the metric term at the end. We'll work that out in time. We seem to have ''partially'' created a quantum Bianchi identity by understanding the commutation written in the form
So question is, what notation do we use to express commutation on the first and last cyclic Riemann terms? This serves as a lead forward.
Let's make a clearing in the forest with some work. I have now written out the full form of the Bianchi identities. Doing so, I was hoping to see if it reveals anything.
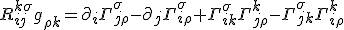
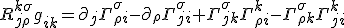
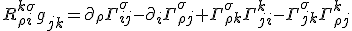
Again, this needs to satisfy a Bianchi identity
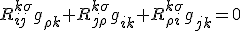
which we recognize as one of the forms of the spacetime uncertainty locked in equation 2. In the last Cyclic Riemann tensor, is a
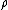and 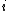indice - note this is an edited correction for right form, check next post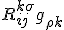
Without the metric, this is just
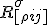
and the brackets and the indices inside of them denotes the antisymmetric parts which involves
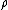and no other space derivative interestingly, at least, from the first definition. Notice then also, when we worked out the Bianchi identities in full form, we could see commutation relations between the time and the space indice -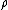 
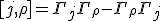
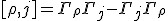
Maybe there is a connection there, maybe there isn't - but its nice to write them down and identify some of the commutation relationships leading to those quantum Bianchi identities.
Post by: Dubbelosix on 08/09/2017 03:41:52
It seems I have done this last Bianchi identity incorrectly ... when you do it right (I mixed up the last indice wrong) then you do not get commutation with
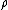and 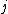- another good reason why double checking your indices is a good idea. The form this Bianchi identity takes is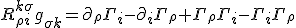
So be mindful of this mistake and that it has been fixed.
Post by: Dubbelosix on 08/09/2017 03:50:35
It seems I have done this last Bianchi identity incorrectly ... when you do it right (I mixed up the last indice wrong) then you do not get commutation with
So be mindful of this mistake and that it has been fixed.
The full corrected form is
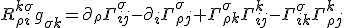
Post by: Dubbelosix on 08/09/2017 04:01:10
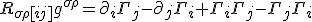
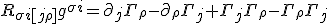
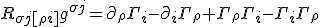
You can write these three relationships out in the Bianchi identity, we can write the commutation again, on the indices
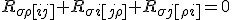
The order of the commutation with respect to indices we have looked at have revealed their commutation in the last two indices.
Post by: Dubbelosix on 10/09/2017 02:49:20
Now we can move on to the three important identities we looked at and they will give a quantized look at the identities.
You can write these three relationships out in the Bianchi identity, we can write the commutation again, on the indices
The order of the commutation with respect to indices we have looked at have revealed their commutation in the last two indices.
Considering, that from the first quantum Bianchi identity we created, with extra indices, it is common to construct a 1/2-tensor
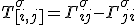
Which we identified much earlier on is an object which describes the curvature and even implies a torsion. Is it possible to construct similar tensors from the cyclic quantum Bianchi identities?
Post by: Dubbelosix on 10/09/2017 02:59:50
Post by: Dubbelosix on 11/09/2017 03:47:08
In a similar theory, a superpositioning of a mass acts like a static gravity. Wave function in Hilbert space allows a superpositioning of geometry!! This approach requires that there exists a form of a static Schrodinger equation. The lack of any acceleration for a geometrical theory is important for the pre-collapse state. Stationary Schrodinger states do exist. Consider a wave with derivatives in space and derivatives in time,
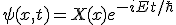
The probability is
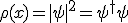
You can identify the relationship:
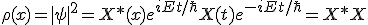
The location of the particle, and its mass, will tend around the absolute square value (collapse). One reason to see this as a stationary solution, is because for the very fact it is time-dependent. You can create an operator:
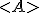
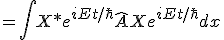
Which is an expectation value and has a domain
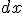and has used the time evolution operator 
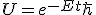. In which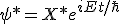
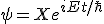
The Problem of Time Dependence
A stationary theory of the gravity does lead to a problem if we consider there is a special non-trivial spacetime relationship (which hints at a time dependence). In which case, we expect there to be a relationship of the form
(unable to put into dirac notation due to site sensitivity to latex)
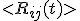
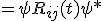
(some notation latex here does not like)
This physically doesn't make sense, because the dependence of time invites that the geometry is changing with time, when by a restriction of physics, it has to be static.
The purely static case of the expectation value of
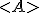
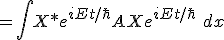
(in which X is a function associated to spatial derivatives). would reduce to just the spatial derivatives
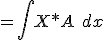
The static solutions are nothing but the time-independent Schrodinger equation (!), which is just
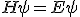
A suitable attempt would be to look for time-independent Hamiltonians
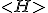
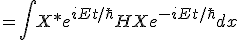
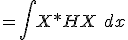
We know what
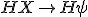. This gives simply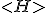
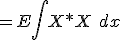
If the wave function is normalized, the last terms
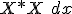come to 
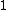. That is, the expectation is just the rest energy of the system of the stationary system. Consider the square of the operator:
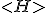
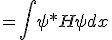
This will give
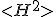
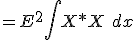
Which leaves the square of the energy. If we understand this as an operator of the form
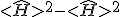then we have unearthed an important feature about the static system. The difference of the square of the energy yields there is no uncertainty in the system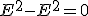
Notice we have uncovered there is no uncertainty in the geometry of spacetime (if this previous solution holds) for a static theory.
So we have some important questions.
1. Is quantum gravity time-dependent?
2. Do superpositioning of particle states give rise to stationary systems?
To understand why the first question is important, is because if we are arguing for a non-trivial spacetime solution then the geometry is necessarily time-dependent (which may in hindsight appear like an odd thing to say), but the issue of time is a non-trivial one itself - some argue that it doesn't exist.
The static field depends though on a situation: The static theory depends that there is a perfect equilibrium in the system. However, it must also be noted that the particles mass is not quite evenly distributed. In fact, the actual mass of the system will tend around the square of the absolute value of its wave function, so we could argue that there cannot be a true equilibrium.
Can we interpret the square of its wave function as the center of mass in which small variances occur? It would be interesting if gravity coupled to a superpositioning principle for matter may lead to a gravitationally-induced collapse of the system (an idea no less) that Penrose himself has peddled since around 1995.
I found an interesting article that seems closely related to our discussions:
''Even though there is an essential uncertainty in the
energy of the superposition of different space–time geometries,
this kind of energy uncertainty is different in nature from the
energy uncertainty of unstable particles or unstable states in
quantum mechanics (Gao, 2010).''
http://doi.org.ololo.sci-hub.bz/10.1016/j.shpsb.2013.03.001
The article further says:
''The former results from the ill-definedness
of the time-translation operator for the superposed
space–time geometries, while the latter exists in a definite space–
time background, and there is a well-defined time-translation
operator for the unstable states.''
We too covered a problem when transposing our theory of gravity to a Hilbert space, that a stationary theory of superpositioning won't hold for the spacetime uncertainty principle. We have argued also though, that maybe there is no true perfect equilibrium in the system.
Certainly, for the static case of a wave function around a nucleus, it cannot exist as a true static system because the atom has to give up its energy eventually (unless subjected to a Zeno effect). Though Bohr has attributed it to a special orbit, this is very vague explanation of an otherwise, interesting phenomenon. Most people generally believe for instance, the radiation of an electron to a lower orbital is a spontaneous phenomenon. In all my investigations of quantum mechanics over the years, nothing in physics has made me convinced anything is by chance. There will be an underlying physical reason why an atom will give up its energy eventually, a phenomenon we know as quantum decay.
Post by: Dubbelosix on 11/09/2017 04:09:56
Post by: Dubbelosix on 11/09/2017 05:33:21
''The superposed lump plays the role of the Schrodinger’s cat. Supposing the gravitational field of the lump and that each lump location separately represents a stationary state and that energy in each case is the same, can we conclude that the quantum superposition of the two lump locations is a stationary state? Penrose using the profound conflict between general covariance principle and superposition principle, asserts that gravity is responsible for an objective reduction of quantum states, accordingly such superposition is not stationary and collapses (Penrose 1996).''
'' General covariance principle implies that in absence of any spatial inhomogeneity in the background potentials, there is nothing in the intrinsic nature of the lump location that allows us to distinguish it from any other lump location, whereas to sense the quantum superposition of lump locations, those locations must be distinguishable. In other words, to have just a single Schrodinger equation governing the evolution of the superposed quantum system, we have to identify those two space–times and according to the general covariance principle there is no canonical way of asserting which point of one space–time is to be regarded as the same point in another. ''
https://link.springer.com/article/10.1007/s40995-016-0024-9
Post by: Dubbelosix on 11/09/2017 20:20:00
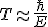
And in the Penrose model, the energy is given as
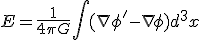
We can derive a more general case that can be used to measure the density variations of spacetime. Deriving the gravitational binding between any coherent gravitational superpositioning state can be given the following way:
The gravitational field inside a radius
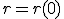is given as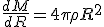
and the total mass is
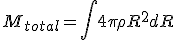
and so can be understood in terms of energy (where
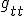is the time-time component of the metric),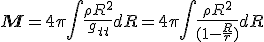
The difference of those two mass formula is known as the gravitational binding energy:
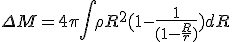
Distribute c^2 and divide off the volume we get:
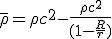
Were we have used a notation
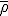for the energy density. Fundamentally, the equations are the same, just written differently. Notice that 
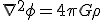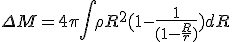
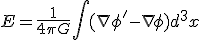
from Poisson's formula, in which we notice the same terms enteringSo while Penrose suggests calculating the binding energy directly from the gravitational potential
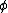there are ways as shown here, to think about it in terms of the gravitational energy density and the gravitational binding between the two. Now, J. Anandan has postulated an equation with dimensions of energy
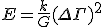
He postulates a fluctuation of the connection
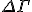and proposes the gravitational fields of the superpositioned states may be regarded as peturbations on the background Minkowski spacetime and suggests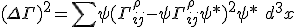
Where we have removed Dirac notation because of the sites sensitivity to certain symbols and format. It's an interesting equation that needs to be understood better for it shares formal similarities to the approach we took in a Hilbert space:
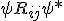
As an expectation value on curvature tensor. When we think of a connection like
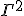really, what is being suggested, is a covariant derivative and a connection term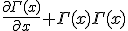
and with the indices and extra terms, it just becomes a more complicated object known as the curvature ternsor
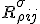. In theory, we should be able to replace 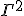for the curvature tensor. http://sci-hub.bz/10.1007/BF02105068
Post by: Dubbelosix on 11/09/2017 20:56:02
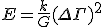
He postulates a fluctuation of the connection
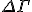and proposes the gravitational fields of the superpositioned states may be regarded as peturbations on the background Minkowski spacetime and suggests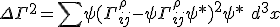
Where we have removed Dirac notation because of the sites sensitivity to certain symbols and format. It's an interesting equation that needs to be understood better for it shares formal similarities to the approach we took in a Hilbert space:
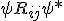....''Let's explore this first equation by Anandan by studying the dimensions. I thought what was supposed to be implied here from his 'proposed' constant of proportionality, was the speed of light to the power of four, which is an equation with dimensions identical to an energy of the form
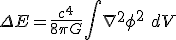
So while the author did not specify, did they set
to natural units and keep the definition of the Newtonian constant in there?The equation does have non-commutative properties in
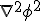it should be noted. Taking both equations and looking at the structure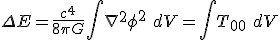
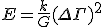
The equations are very similar.
Post by: Dubbelosix on 11/09/2017 23:01:59
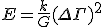
doesn't make much sense to me... I mean, I could very well be wrong or missing something. I did try and construct some kind of meaning out of it though.
So what is the difference between the two equations?
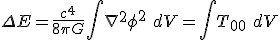
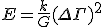
Firstly, I should have noted that the first equation uses a dimensionless interpretation of
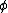which you can expand in a series, which can be thought of as ''gravitational corrections.'' Knowing that the operator has dimensions of inverse length squared 
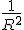and since the first term is a gravitational force 
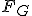, we end up with an equation (with dimensions of 
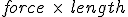which is exactly the dimensions of energy. Going to the second equation I am wondering if there is a typo in the equation and really what we want is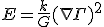
can be written also then as
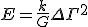
We may identify the squared value of the divergence
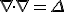is the Laplace operator. This means his equation can be written as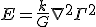
Now compare
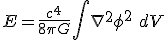
An integral on the RHS of the first equation will yield
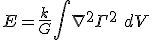
Which does have dimensions of energy iff the connection is of dimensionless form and the missing constant of proportionality is
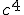to fix the dimensions. So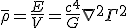
Is an energy density and the energy is simply
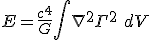
Is it possible that such a mistake occurred somewhere? Because the other form doesn't make much sense to me.
Post by: Dubbelosix on 12/09/2017 00:11:41
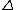may not be the Laplacian. It seems at least, from his fluctuation equation, it could be like a difference operator, in which case, we don't usually square it. The similarities though, were interesting. Even if it was a difference operator, the dimensions of his equations would not make sense to me. So... really, we can replace the ... inspiring
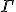for the curvature tensor itself. The difference in quantum geometries in a Hilbert space is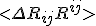
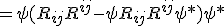
*Check this with the early construction!
Where we have used
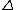as a difference operator, in the same manner it seems, as Anandan. In his equation, an element volume term is attached to it, why, I am not sure. We have kept it out of this definition. The equation just proposed, is the proving ground of unitarity and whether the system obeys it. This equation doesn't tell you whether it does.Post by: Dubbelosix on 12/09/2017 00:24:35
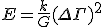
Is not treating
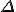as the Laplacian, but instead a difference operator, and if 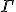now has conventional dimensions of 1/length then an integral yields a true energy equation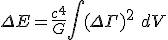
Which would make sense of the element volume attached to his curvature/geometry probability difference and in a case where he set
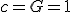. In which case, you should still be able to write the following: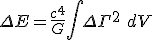
Where we do not square the operator this time.
Post by: Dubbelosix on 12/09/2017 01:29:20
Post by: Dubbelosix on 12/09/2017 02:32:17
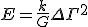
with
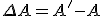as the difference operator.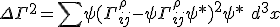 We have established, what is really meant with equation 1. is
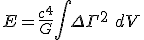
We have argued, that the squared component of the connection can be interpreted in terms of the curvature tensor. This is related to the difference of geometries and that is given now as a full energy equation with
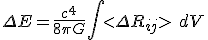
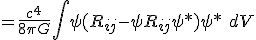
Post by: Dubbelosix on 13/09/2017 07:24:01
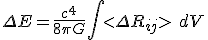
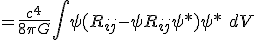
Shares the difference between two expectation values of the system:
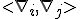
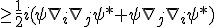
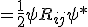
That coefficient of
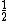may indeed attach to that energy, just like a kinetic energy term. So really, when you saw this object: 
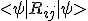as we have shown, we had already calculated this identity very early on in the work. So the energy equation is compatible in a Cauchy-Schwarz interpretation of spacetime.
Post by: Dubbelosix on 15/09/2017 11:52:53
In terms of a Laplacian, it was possible to construct an equation of the form: Again, some of these equations have been pulled out of their code because of site sensitivity to Dirac notation.
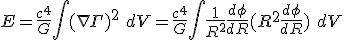
which does not have a squared value for the Laplacian
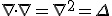. The funny thing is ... again, it all led to the same end anyway. Notice though, even if it was a Laplacian, you would not be squaring the Laplacian because dimensionally, that makes no sense. You could square the nabla operator and argue the wrong notation was used, but since the same notation crops up all over the internet, I must still assume it is a gap in my knowledge. (\Delta A)^2 = <\psi| A^2| \psi> - 2<A^2> + <A^2> = <A^2> - <A^2>
You can see the equivalent of equation 2. in the quote as
<A> = \sum_n <\psi | a_n > <a_n|\psi> a_n
= \sum_n <\psi | A | a_n><a_n|\psi > = <\psi| A (\sum_n |a_n ><a_n|) a_n |\psi> = < \psi| A |\psi>
Which makes use of the completeness theorem. To find the alternative version, you square and solve from the form involving eigenstates: Using their notation ~
(\Delta A)^2 = \sum_n <\psi | a_n > <a_n|\psi> ( a_n - <A>)^2
= \sum_n < \psi | a_n><a_n |\psi>(a^2 - 2a_n<A> + <A>^2)
= \sum_n <\psi| a_n> <a_n |\psi> a^2_n - 2<A>\sum_n <\psi |a_n><a_n| \psi> a_n + <A>^2 \sum_n <\psi|a_n> <a_n |\psi>
So that's how those strange extra symbols come into the game, even though they were never implied in the formulation of our Cauchy Schwarz spacetime.
Right... back to the work.
How do you vary the expectation value in the equation
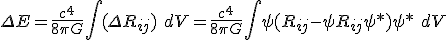
The total variation will split this part up
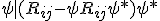
into
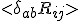
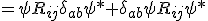
where the subscript of
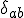denotes a ''two particle system.''
Post by: Dubbelosix on 15/09/2017 12:26:55
...
where the subscript of
Take careful note though, this last equation is only for one variation in one such term for the expectation
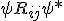- so you will end up with a four component equation in a superpositioned system of two particles or by calculating the binding energy, which also invites the differenece of two expectations.
Post by: Dubbelosix on 15/09/2017 12:34:21
But now the reference, or you won't know what the hell I am talking about.
http://physics.mq.edu.au/~jcresser/Phys301/Chapters/Chapter14.pdf
Post by: Dubbelosix on 16/09/2017 00:19:16
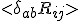
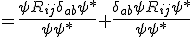
The reason why we would want to do this is because it would make the expectation independent of the normalization of the wave function. Also expect there to be a variation in curvature tensor on the right hand side. The variation could possible be written in the following way
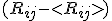.Post by: Dubbelosix on 17/09/2017 19:27:54
Right... back to the work.
How do you vary the expectation value in the equation
The total variation will split this part up
into
where the subscript of
Let's construct the full equation now. Expand the equation a bit on the right hand side and setting
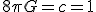and also taking 
as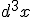 
, which seems to be a common practice,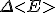
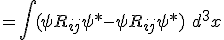
When you vary the wave function for each term, you get the full equation
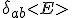
(again, devoid of Dirac notation due to site sensitivity to latex).
Even though we think about
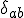as some differential change between two particle systems, in the context of the right handside, its actually the difference between two geometries of two particles - previous to the collapse state, that one particle is smeared though space. This has been the context of our investigations and how to view gravity.
Post by: Dubbelosix on 19/09/2017 02:26:31
Not sure if all these equations will show, the place seems sensitive to certain latex equations. If it doesn't work, I will take it out of its latex code so you can translate it.
To give a hint in how to do this unification attempt, we have three key equations,
1.
These are the exact Christoffel symbols of the antisymmetric tensor indices
2.
This was an equation derived by another author, finding the relationship in a different form argued from quantum mechanics. As you will see in key equation 3. the form has similarities to application of a Hilbert space ~
3.
\sqrt{|<\Delta X_A^2>< \Delta X_B^2>|} \geq \frac{1}{2} i(< \psi|X_AX_B|\psi > + <\psi|X_BX_A|\psi>) = \frac{1}{2} <\psi|[X_A,X_B]|\psi>
Again, this is a Hilbert spacetime commutation relationship of operators which has to translate into the gravitational dynamics dictated by key equation 1.
So let's put it altogether, its just like a jigsaw puzzle now. Implemented the Christoffel symbols in approach 1. into approach 2. we get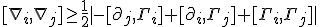
In the framework of the Hilbert space it becomes - assuming everything has been done correct, takes the appearance of ~
\sqrt{|<\nabla_i^2>< \nabla_j^2>|} \geq = \frac{1}{2} i(< \psi|\nabla_i\nabla_j|\psi > + <\psi|\nabla_j\nabla_i|\psi>) = \frac{1}{2} <\psi|[\nabla_i,\nabla_j]|\psi> = \frac{1}{2} <\psi | R_{ij}| \psi > = \frac{1}{2} < \psi |- [\partial_j, \Gamma_i] + [\partial_i, \Gamma_j] + [\Gamma_i, \Gamma_j]| \psi >
without imaginary number on
I was told by my friend my Hilbert space would be infinitely dimensional, I don't think this is the case at all, after more studying. The L^2 function implies finite results in the Hilbert space and L^2 space has functions which satisfy Cauchy Schwarz inequality. Since we formulated a spacetime theory using the Cauchy Schwarz inequality, it seems reasonable to assume this is finite dimensional.
http://mathworld.wolfram.com/L2-Space.html