Naked Science Forum

On the Lighter Side => New Theories => Topic started by: jeffreyH on 12/10/2017 13:00:39

Title: A quantum diary
Post by: jeffreyH on 12/10/2017 13:00:39

This is most definitely not going to be a theory. I am going to document my study of quantum mechanics. A sort of learn by teaching. Hopefully someone else may benefit.

Title: Re: A quantum diary
Post by: jeffreyH on 12/10/2017 17:48:26

In the mid 1920s when Werner Heisenberg was formulating his ideas on quantum mechanics, Max Born applied matrices to the problem and the result was matrix mechanics. An equation arose from these investigations.



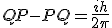
Here Q is a matrix representing position and P is a matrix representing momentum. The products of the two matrices do not commute. That is QP does not equal PQ. Behind this is the idea that if you can measure position exactly then there is no way of measuring momentum exactly. This may seem counter-intuitive but then that is quantum mechanics.

Title: Re: A quantum diary
Post by: jeffreyH on 12/10/2017 17:59:28

Matrix mechanics uses linear algebra. However, I am going to keep things simple. I won't be explaining linear algebra.

In the previous equation the letter i appeared. This represents 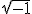which is an imaginary number. This is also used in the definition of complex numbers which have both real and imaginary parts. Both of these concepts are used in quantum mechanics.

Title: Re: A quantum diary
Post by: jeffreyH on 12/10/2017 18:15:32

When defining matrices it is usual to use uppercase Latin letters. As in A or B. Single numbers, called scalars, are represented by lowercase Latin letters as in x or y. Vectors can also be represented by lowercase letters but must be distinguished by something, like that.

Title: Re: A quantum diary
Post by: jeffreyH on 13/10/2017 21:46:00

After Heisenberg's original work Wolfgang Pauli defined a set of matrices that are used to determine particle spin and magnetic moment. They are as follows.







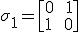
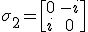
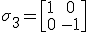
The latex leaves a lot to be desired so you can read more here.
https://en.m.wikipedia.org/wiki/Pauli_matrices

When each of these matrices are multiplied by themselves, that is squared, the result is a matrix known as the identity matrix. This is equivalent to the number 1 in terms of multiplication. Since multiplying any number by one leaves the number unchanged. Hence the name identity.

https://en.m.wikipedia.org/wiki/Identity_matrix

Title: Re: A quantum diary
Post by: jeffreyH on 14/10/2017 08:34:52

The Pauli matrices are used to represent the spin angular momentum or magnetic moment of an electron or proton or similar particle. These type of particles have spin 1/2. Spin angular momentum is a vector quantity. Its projections in 3 perpendicular directions are represented by the following matrices.









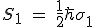
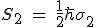
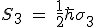
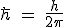
Here h is the Planck constant.
https://en.m.wikipedia.org/wiki/Planck_constant

Title: Re: A quantum diary
Post by: jeffreyH on 14/10/2017 09:06:18

So what do we and up with as the contents of our S matrices? Well all elements are multiplied by .







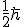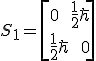
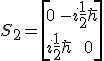
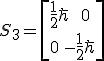
Notice that our second matrix includes the imaginary number i. This is important and is incorporated into the rules of quantum mechanics.

Title: Re: A quantum diary
Post by: jeffreyH on 14/10/2017 10:11:16

So how do we multiply matrices together? A matrix has columns and rows. Say we have the multiplication of matrices A and B. We can only multiply them when the number of rows in B equals the number of columns in A. Let's try multiplying the previously defined matrix S₁ with itself. It has 2 columns and 2 rows. So it obeys the rule. Let's break it down.

Multiplying the matrix by itself will result in another 2 by 2 matrix. So how do we get there? We take the first row of the first matrix and multiply its elements by those in the first column of the second array. Adding the individual products together.

S₁[0,0] x S₁[0,0] + S₁[0,1] x S₁[1,0]

If our new matrix is X then the above would give us the value of X[0,0]

The full set of 4 equations are as follows.

X[0,0] = S₁[0,0] x S₁[0,0] + S₁[0,1] x S₁[1,0]
X[0,1] = S₁[0,0] x S₁[0,1] + S₁[0,1] x S₁[1,1]
X[1,0] = S₁[1,0] x S₁[0,0] + S₁[1,1] x S₁[1,0]
X[1,1] = S₁[1,0] x S₁[0,1] + S₁[1,1] x S₁[1,1]

One important point to note. The indexes are [row, column].

So what do we get in our new matrix?



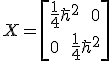
So what will we get if we square matrices 2 & 3?

Title: Re: A quantum diary
Post by: jeffreyH on 14/10/2017 11:26:19

Since, as mentioned above, any Pauli matrix that is squared results in the identity matrix. So all the S matrices squared will have X as their result. The identity matrix itself is considered a Pauli matrix itself so it too can produce an S matrix that we shall call S₀. When multiplied by our factor and squared this results in matrix X.

What does all this mean? Well it is a lesson in probability. It is also artificially contrived to demonstrate a point.

Matrices can be added together as well as multiplied. The equivalent elements of each matrix are added together to obtain the elements of the result. So for matrices A and B with two rows and two columns, adding them together to give X will be done as follows.

X[0,0] = A[0,0] + B[0,0]
X[0,1] = A[0,1] + B[0,1]
X[1,0] = A[1,0] + B[1,0]
X[1,1] = A[1,1] = B[1,1]

What would happen if we added our 4 S matrices together. The non zero elements have one quarter of a value in them. That is 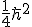so those values will sum to 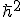. That is 100% of the value instead of the 25% in each element.

I said this example was contrived and we will see better examples soon but now it is time to look at probability.

Title: Re: A quantum diary
Post by: jeffreyH on 14/10/2017 11:53:14

For those with a more technical interest see here.
https://en.m.wikipedia.org/wiki/Spin_(physics) (https://en.m.wikipedia.org/wiki/Spin_(physics))

NOTE: If you have read through the above article you will have seen that spin is quantised in units of the Planck constant h.

Title: Re: A quantum diary
Post by: jeffreyH on 14/10/2017 22:08:21

A vector is a matrix with only 1 row or 1 column. As long as a 1 row matrix has more than one column and visa versa for the one column matrix. So if we have a vector x we can define it like this.

x[0] = 2
x[1] = 3
x[2] = 6

The magnitude of this vector is defined as follows.



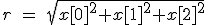
Now what has this got to do with probability? Well let's define some other values u₀, u₁ and u₂ and three equations.





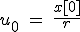
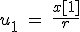
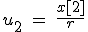
Then



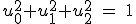
Let's try it by plugging in the numbers.





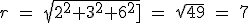
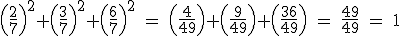
So all the parts add up to 1. That is 100%.

Title: Re: A quantum diary
Post by: jeffreyH on 07/11/2017 21:08:55

Since I am busy at the moment some light reading for those interested.
https://en.m.wikipedia.org/wiki/Matrix_mechanics

Title: Re: A quantum diary
Post by: jeffreyH on 29/11/2017 13:04:37

What is a Hamiltonian? Find out here.

https://en.m.wikipedia.org/wiki/Hamiltonian_(quantum_mechanics)
 (https://en.m.wikipedia.org/wiki/Hamiltonian_(quantum_mechanics))

Title: Re: A quantum diary
Post by: jeffreyH on 16/12/2017 11:18:10

The basic rules of quantum mechanics in matrix form involve the quantities describing physical systems. These include velocity, momentum, angular momentum and energy. Each one of these quantities is represented by a matrix. These matrices are all the same size so they can be added together or multiplied. An example is the equation for position and momentum discussed earlier.


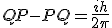
To quote from Quantum Mechanics in Simple Matrix Form by Thomas F . Jordan P 57
"Quantum mechanics makes a distinction between a quantity and its values. In any situation, depending on what has been measured, some quantities have definite values and others do not. Therefore algebraic equations relating different quantities are not generally written in terms of their values."

Why? Due to the uncertainty in measurement. To quote the next section from Jordan.
"We consider the state of the system in a particular situation, which means all the information about a particular system at a particular time. For each quantity there are probabilities for the different possible values. For a quantity that has a definite value, the probability is 1 for that value and 0 for the other possible values. For a quantity that does not have a definite value, there are nonzero probabilities for more  than one possible value. For every quantity there is a mean value corresponding to the probabilities."
We saw earlier how we can arrive at the value of 1 using vectors. Next I will discuss the mathematical form of the rules.