Post by: JH on 01/05/2020 13:44:24
This means that I must get it out of my system and into the public view. ‘Certainty’ is for those having all the answers, I do not have them all so I did the brave thing, I published online, everything I have got, oh dear.
Now I invite curious, skeptical passers by to poke holes in it, help with some necessary cleaning up, and hopefully further promote the insight, I alone can't fix it. It is not for everybody though, you probably have to suit up for a good hike, my imagination took me to lower earth orbit.
Let's see if this insight survives the criticism and seems ready to promote from ‘New theory’ to ‘Mainstream science’.
If you are interested to take a peek, and maybe even join the effort to falsify, I will be very happy to welcome you on my blog <link to personal site removed>.
Thank you for your kind attention, but don't let that friendliness keep you from uttering firm criticism. Slap on the shoulder is also appreciated ;)
Cheers, JH
Post by: Halc on 01/05/2020 14:10:17
State whatever arguments you wish to make here and don't make us go looking for them.
Post by: Bobolink on 01/05/2020 14:19:43
Let's see if this insight survives the criticism and seems ready to promote from ‘New theory’ to ‘Mainstream science’.Looking forward to seeing your ideas.
Post by: JH on 01/05/2020 23:12:39
@Bobolink Let me recompose myself from the previous ‘boo-boo link’ mishap for a moment. I feel like an amateur, but that seems to be the reason why I seek advice in the first place ;). Now “Looking forward to seeing your ideas.” is quite a daunting prospect, and I have to contemplate how to do so in an orderly fashion without merciless attempting to republish scripture in two breathless posts
I named de hypothesis 'On the Volume of Number'
Let's start with my initial observation that kicked of this journey, seems to make the most sense
The zeta function for s=2 is the infinite sum of reciprocal squares of the natural numbers :
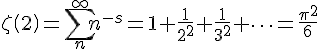
The sum formula adds up to
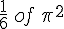. Note that the closed form 
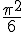indicates that the rational squares add up to a fraction of an irrational surface with sides 
.
Share Figure 1.1 The sum formula.GIF (9.91 kB . 648x255 - viewed 3298 times)It is in precisely this mapping that an alternative pathway for investigation presented itself.
Volume over zeta
A proportional symmetry, analogues to the inverse square law, exists between the result
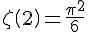and the spherical volume enclosed by a surface area 
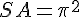, expressed as twice the radius of such a volume.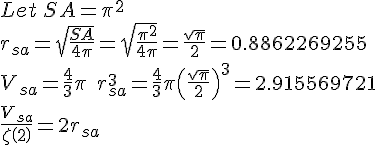
The structure of Volume over zeta
The value volume over zeta is exactly twice the radius calculated for a sphere with
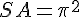. The function value 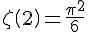represents a ratio which seems to sit in the middle of some dynamic process involving the expansion of a sphere. This becomes clear if we dissect the structure.The ratio
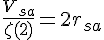has the form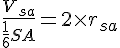
Assume that
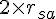is proportional to the radius of some next volume, the infinite sum of 
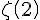can be interpreted as the process that completes the inflation (by doubling of radius) from 
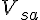up to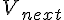 
. The assumed inflation has to start from some initial volume.Etc. etc.
So far my initial observation. From this I will construct a mapping function based on the triangular numbers, and in doing so already sketch an outline of the proposed solution ‘all non trivial zeros have real part one half’.
In the hypothesis I will construct a tool, the ‘Quadrature Geometric Framework’, this will be a geometric model of a complete convex set. Application of this model on a repository of potential will reveal how the QGF is emerging from excitation of the repository. The proposition is therefore that the QGF is the model for a first principle that allows structure to arise in an homogenous field that becomes excited.
The catch is that the QGF is NOT some real (Platonic) abstract object ‘out there’, it clearly is an abstraction derived from measurement of an existing physical system. 'Clearly' because in modeling the abstraction, the geometry of the QGF exceeds the bounds of the convex set, which is like exceeding the bounds of the physical universe, and therefore nonsensical.
If, however, the geometry is interpreted as bouncing back on ‘the boundary’ of this convex set, then we find a range of values, the geometric primes or density primes. These are not primes in the regular sense, but ‘behave’ as such, and show how this set can be envisioned to behave like primes in a physical sense.
That this must be true is because the set in numerical order of appearance does project 1 on 1 (slight adjustment in amplitude) with the Montgomery-Dyson pair correlation formula.
share of Figure 7.7 Geometric Primes and Pair correlation.PNG (218.06 kB . 1102x621 - viewed 3279 times)And thus corresponds to the non trivial zeros of the Riemann zeta function, coming there in a roundabout way. In fact, the distribution of the zeta zeros is geometrically ‘proven’, but to get there I have to convince the lot of you, in chapter 3, that Q=R, so I hope you do not leave the party at that point, and continue on with me (pun intended).
I know that I know nothing, but maybe also in a more literal sense. This is some intense confrontation, your all 'naked scientist' and I feel exposed.
I think I leave it at this, have to type with my left hand, bummer.
Post by: Bobolink on 02/05/2020 01:57:47
Let's start with my initial observation that kicked of this journey, seems to make the most senseI am not sure what I am supposed to get from this. In this first part are you just discussing the zeta function or is there some specific point? I could not view your .gif file, it came out garbage.
The zeta function for s=2 is the infinite sum of reciprocal squares of the natural numbers :
The sum formula adds up to . Note that the closed form indicates that the rational squares add up to a fraction of an irrational surface with sides .
Share Figure 1.1 The sum formula.GIF (9.91 kB . 648x255 - viewed 40 times)
It is in precisely this mapping that an alternative pathway for investigation presented itself.
Post by: JH on 02/05/2020 11:04:49
I could not view your .gif file, it came out garbageDo both figures, as also the Mathjax not render on your end? I downloaded both figures, they seem to open fine. Ah well, maybe something technical I am missing, being a newbie and all.
Your not missing much though, I merely observed that
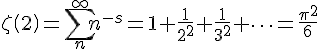, and that the function value can be graphically represented as depicted in inclosed Figure 1.1.Let's see what happens if I just choose the files and do not embed them manually.
Post by: Bobolink on 02/05/2020 13:55:40
OK. I still have this question: I am not sure what I am supposed to get from this. In this first part are you just discussing the zeta function or is there some specific point?I could not view your .gif file, it came out garbageDo both figures, as also the Mathjax not render on your end? I downloaded both figures, they seem to open fine. Ah well, maybe something technical I am missing, being a newbie and all.
Your not missing much though, I merely observed that
Let's see what happens if I just choose the files and do not embed them manually.
Post by: JH on 02/05/2020 14:56:07
It is in precisely this mapping that an alternative pathway for investigation presented itself.
I am not sure what I am supposed to get from this.
Well, what can I say, as deep as I guess light can travel on this issue ;)
Let me ponder on this formulation for a while, but I am afraid I reached my limit on literary skills.
Post by: Bobolink on 02/05/2020 17:16:51
Post by: JH on 05/05/2020 00:04:28
Presentation Title: On the Volume of Number
Research focus: Riemann hypothesis, alternative approach Quadrature Geometric Framework.
School: NA (Private research project)
Presentation Type: Blog [XXXXXXXX].com
Abstract (draft)
Euler found the closed form of the sum of reciprocal squares to be
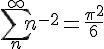and later observed that the sum over integers equalled a product over the primes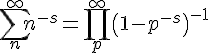 
Riemann found a way to extend this number theoretical problem into one that can be studied with the geometric tools of complex analysis, for which the notation
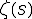is used, Zeta of s. The Riemann hypothesis states ‘All non trivial zeros have real part one half’, and has yet to be proven.The Montgomery-Dyson pair-correlation function indicates a correlation between the spacing of the zeta zeros, the eigenvalues of a random Hermitian matrix and, for instance, the energy levels in a heavy nucleus like U-238. These systems do adhere to a underlying mathematical structure that will be identified in this paper. Insight into the distribution pattern of the zeta zeros might lead to major advances in science by revealing something about quantum physical systems and the ‘unreasonable effectiveness of mathematics’ in science.
An analysis of the sum of inverse squares, lead to the discovery of an apparent underlying abstract spatial structure, with properties that further suggested the involvement of some dynamic process. These spatial aspects and the ‘dynamic’ process can not be properties of the abstract sum of inverse squares. The sum of inverse squares, i.e. mathematics in general, is hypothesized to be contingent on a physical state, and points to the existence of a first principle that emerges as direct consequence of the topology of given physical state.
A new geometric tool is introduced, the Quadrature Geometric Framework (QGF), based on the properties of a convex set.
Results
The model shows a clear distribution pattern of the zeta zeros, which pattern confirms the Riemann hypothesis.
The QGF density primes are a compressed subset of the zeta zeros, the distribution model of the zeta zeros is identified and the complete set of zeros is accounted for.
A counter argument for the continuum hypothesis is presented that shows a mechanism that appears to put the sets of
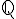in a one to one correspondence with 
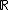. This mechanism is integral part of the QGF and defines the boundary condition for the convex set and is derived from the primorial function.Presented is a prime stack, based on the primorial function which gives insight on both the distribution of prime numbers, and a mechanism that models the boundary conditions of a shockwave traversing the repository of potential.
The shockwave acts as a phase shift, it presents an area of constant temperature and pressure which is recognized as zero point energy. The propagation wave is hypothesized as dissipating (entropy), the phase shift, however, is recognized as a repository of energy of fixed size, and underlies the local stability of matter, appearing to contradict entropy.
Conclusion
The QGF density primes can only exist in the context of a physical state. The QGF is modelling the underlying principle of spacing cq particle repulsion as predicted by the Montgomery-Dyson pair correlation formula. The QGF is a model for a physical instance of a complete convex set, the universe. The QGF does not have explanatory power concerning why there is something rather then nothing, but the QGF model is directly contingent on the instantiation of a physical state with elastic border conditions, which implies the preferred state of such a repository.