Post by: Eternal Student on 14/08/2021 02:01:38
This section of the forum has gone a bit quiet as of late. Here's a question that should be open to everyone who has studied Physics at school level. I'm interested in all answers and opinions. You can talk about what you know from University if you wish but the main focus (for me) is on what I can say or present to a school-age audience. What is the best way to answer questions like this from a child in school?
Background When you were at school you may have studied some Physics. How were you taught about gravitational potential energy? Did it seem sensible to you? You may have seen examples like the following:
/\
/ || \@
/ || \
||
This thing is a tree.
@ <--- This thing is an apple in the tree.
What follows next is a beautifully animated diagram of the apple falling from the tree and gaining kinetic energy as it falls....
(You just have to imagine that part).
It would have been said that the apple had gravitational potential energy while it was up high. This potential is converted to kinetic energy as it falls. OK, remember that?
- - - - - -
Questions to focus on:
(i) Were you taught that the gravitational potential energy was IN THE APPLE ?
(ii) Did you believe it? (I did while I was at school).
(iii) Was there anything different about the apple when it was up high or just that it was up high?
(iv) If the energy was in the apple, then did it have more mass when it was up high?
(v) You may have studied more physics since school. Where do you now think the gravitational potential energy is located?
(vi) How would you go about explaining this concept to a school-age student, maybe one of your own children if you have them? Suppose they ask directly "where is the gravitational potential energy stored?" - what will you tell them?
Thanks for your thoughts and opinions. Best Wishes to everyone.
Post by: Halc on 14/08/2021 05:02:34
It would have been said that the apple had gravitational potential energy while it was up high.I was taught that potential energy is negative, so it has greater magnitude negative energy after it falls to the ground.
Typically in early (7th grade) physics, concentration is on Earth-local environments where Earth is flat and the gravity is constant at all altitudes. In this environment, PE being negative has little meaning, but they still taught us that.
Quote
(Were you taught that the gravitational potential energy was IN THE APPLE ?I don't remember anybody trying to express it that way. The apple HAS potential energy, which is actually a relation between the apple and something implicit, but in the introductory phases, they didn't express it as a relation.
Quote
Was there anything different about the apple when it was up high or just that it was up high?Pretty much the latter.
Quote
If the energy was in the appleIt has negative energy up in the tree, and negativer (cool word!) energy sitting on the ground. That hardly seems like energy being in the apple.
Quote
then did it have more mass when it was up high?This was introductory Newtonian stuff. Energy mass equivalence was quite a ways off still.
If you drag that in, then the energy/mass is constant all the way since the total energy never changes, so Newton or not, the falling apple doesn't lose mass on the way down.
Quote
You may have studied more physics since school. Where do you now think the gravitational potential energy is located?Relations don't have a location, but the apple has coordinate mass that is a function of its proper mass plus its potential relative to something, plus kinetic/thermal/chemical energy that contribute to coordinate mass, and that mass has a center of gravity which for all practical purposes serves as a location for that PE. Where else would it be? It seems a reasonable answer to give to students.
Post by: Eternal Student on 14/08/2021 13:26:56
About negative p.e.:
Typically in early (7th grade) physics, concentration is on Earth-local environments where Earth is flat and the gravity is constant at all altitudes. In this environment, PE being negative has little meaning, but they still taught us that.7th grade in the US ≈ age 12-13 years ≈ year 8 in the UK.
I'm surprised. We were not taught to consider a negative potential energy until year 12 ≈ age 16-17 years.
None the less, it doesn't dodge the problem. Consider an apple at rest in the tree and also the same apple at rest on the ground. (The potential energy has been converted to heat and sound after the apple bounced about on the floor and that has definitely travelled away and left the apple). Now with both apples at rest the difference is only the potential energy they have. That difference in energy is not exhibited as a difference in mass of the apples.
I agree that mass-energy equivalence may not be on the school syllabus but it's still a little deceitful to suggest that the apple has more or less energy depending on its height. This is something that the students will have to un-learn later at university.
It has negative energy up in the tree, and negativer (cool word!) energy sitting on the ground. That hardly seems like energy being in the apple.I'm not clear on where you thought the energy was, or did you think that energy wasn't something that had to be located anywhere? This isn't meant to be a silly or annoying question - it may be best not to worry about where energy is located and it may be best to teach children that energy doesn't always have a location in space.
- - - - -
Relations don't have a location, but the apple has coordinate mass that is a function of its proper mass plus its potential relative to something, plus kinetic/thermal/chemical energy that contribute to coordinate mass, and that mass has a center of gravity which for all practical purposes serves as a location for that PE. Where else would it be? It seems a reasonable answer to give to students.Where else would it be? Well, for example, the potential energy could be stored in the earth rather than in the apple. We know that the earth exerts a force on the apple but the apple also exerts the same force on the earth.
If you were able to hold the apple still rather than let it fall then the earth would eventually move to the apple's location. The earth would have been the object that gained kinetic energy and seemed to lose potential energy in this case. If you don't like the idea of holding the apple still then make a minor adjustment to the usual model: We can imagine a really big planet-sized apple falling on to a very small apple-sized earth.
What is special about the apple that allows you to say that the apple has the potential energy? Even using your (Halc) complicated notion about everything being a relation based on positions - doesn't the earth also have that relationship, i.e. the earth also has the potential energy?
OK... I think it's reasonable for a child to suggest that the potential energy is stored in the earth rather then in the apple. If we make the situation more complicated then someone can suggest that the potential energy isn't stored in the apple or in the earth, instead it is stored in the field that exists between them. This is like opening a whole new can of worms (a colloquial phrase meaning - creating more problems as fast as any others are solved).
- - - - - - - -
More general discussion
Thanks for your time Halc. Anyone else have any views? Have we been teaching children about something that isn't tied down to any location and quite possibly just doesn't exist anywhere?
Is gravitational potential energy just a convenient book-keeping tool that allows for a conserved quantity (total energy) to be defined in simple mechanical systems?
Best Wishes.
Post by: Halc on 14/08/2021 14:36:45
Now with both apples at rest the difference is only the potential energy they have. That difference in energy is not exhibited as a difference in mass of the apples.Not in Newtonian mechanics, but in relativity, there very much is a difference in mass of the two.
Quote
I agree that mass-energy equivalence may not be on the school syllabus but it's still a little deceitful to suggest that the apple has more or less energy depending on its height. This is something that the students will have to un-learn later at university.I don't consider that un-learning any more than I had to un-learn how to add velocities when you do it the relative way. The approximations were enough to put a man on the moon. As an engineer, the apple still has the same mass in both places. As a physicist, they don't.
Quote
I'm not clear on where you thought the energy was, or did you think that energy wasn't something that had to be located anywhere?To reword, energy (like velocity) seems to be an abstract concept and abstractions don't necessarily have a location, but if it makes you comfortable to assign a location for the apple's energy (or velocity), what better place than the apple to assign it? But this is just for your own warm fuzzies. I cannot think of any part of physics where the location of energy needs to be entered into an equation to derive some physical description.
Quote
and it may be best to teach children that energy doesn't always have a location in space.I agree with that. As I said, I cannot think of an instance where this location would be meaningful.
Quote
Where else would it be? Well, for example, the potential energy could be stored in the earth rather than in the apple.Touche. PE is (usually) a relationship between two objects, so obviously if it could be in one object, it could also be considered to be located in the other. PE can also be a property of an object, but something like an apple has almost none of that, while Earth has plenty. It is the energy necessary to pull all the mass to zero potential relative to each other. I don't think a black hole has meaningful PE.
Quote
Even using your (Halc) complicated notion about everything being a relation based on positions - doesn't the earth also have that relationship, i.e. the earth also has the potential energy?In relation to what? It has different PE relative to the apple, the moon, sun, or Betelgeuse.
Quote
OK... I think it's reasonable for a child to suggest that the potential energy is stored in the earth rather then in the apple.Seems confusing to me. We've a hydro-energy storage facility out here. When there is excess (cheap) energy available, water is pumped from the river into a storage lake at the top of a hill. At times of high demand, that stored PE is used to meet that demand in excess of the capabilities of local generation plants.
If Earth stored that PE, anybody could extract it. But if the PE is in the water, then only those in control of the water can use it. Just an example where the apple seems the more intuitive place to assign the location of the energy if you feel the need for such an assignment.
Location of energy does sometimes matter. When speaking of a closed system, we're in violation of it being closed if energy leaves the system, so maybe there's a case where the location matters. It's still abstract, since the delimiting of 'systems', closed or not, is an abstraction.
Post by: Eternal Student on 14/08/2021 18:52:18
Thanks for your time, Halc. Feel free to slow down and do something else.
Not in Newtonian mechanics, but in relativity, there very much is a difference in mass of the twoYou may need to explain that to me.
In special or general relativity, inertial mass = gravitational mass = rest mass = the only mass worth worrying about.
How does the position of the apple change its mass?
- - - - - - -
I cannot think of any part of physics where the location of energy needs to be entered into an equation to derive some physical description.1. You mention closed systems at the end of your own post.
2. I can't think of many (or any) good school examples, however I can think of examples for university. A momentum-energy tensor for General relativity. To calculate the momentum-energy tensor for a continuous distribution of energy and momentum (e.g. an ideal fluid), you specify the various components of the 4-momentum flux at every point in space. One of those components is the energy density at that point in space. So, I would say you need to know where the energy is located and it certainly makes a difference - put the energy in a different place and you get a different tensor and then ultimately you will have a different system with its own evoution.
I supose you have the same need to know the location of energy and momentum when you construct a stress-energy tensor for use in fluid dynamics (without needing to include General Relativity in your work).
(I could say more but it's boring and people really don't have to read it. I'd be more interested in what others say).
Best Wishes.
Post by: Halc on 14/08/2021 20:23:42
Feel free to slow down and do something else.To hell with that. You're making me think, which is a rare treat on this site.
Quote
How does the position of the apple change its mass?It seems my comment was exceptionally poor in it wording. I said PE was a relation between two objects, and here I am giving the mass of that energy to one object and not the other.
Looking up some reliable (reviewed) sources, we have two systems: Earth with apple on tree, and Earth with apple on ground. The proper mass of both Earth and apple is the same in both systems, but the system mass of the former (as viewed from infinity) is greater than the system mass of the latter. That implies that any meaningful potential energy location is 'the location of the system' and not the location of the apple at all.
It also implies that the proper mass of Earth is less than the sum of the proper masses of all its components, the difference being the PE property of Earth.
See https://physics.stackexchange.com/questions/29570/does-the-mass-of-an-object-change-as-it-moves-away-from-the-earth
Quote
One of those components is the energy density at that point in space.There you go. Nice example. Energy can have a location. Does an ideal fluid have a PE density? I suppose it does if it is expressed as a deviation from the mean, but it is hardly a relation between discreet objects. The tensor arithmetic must be able to express that where the discreet relationship fails.
Post by: alancalverd on 14/08/2021 22:09:41
Not a serious omission. The potential energy of a spring is "stored" in the mechanical stress of the spring, and of the apple, in the tree that is holding it up. After all, the tree grew and raised the stuff needed to make the apple from the ground to the branch, so work was done that resulted in a downward stress on the branch.
Post by: Eternal Student on 15/08/2021 00:16:30
@alancalverd Wow, I like that idea. There is a mechanical stress or what might have been called elastic potential energy in the tree while the apple is hanging off it's branch. You must have been a fairly smart child to think that gravitational potential energy was stored in the tree. I wouldn't have done that and I've never seen it suggested before.
Sadly, I think you could quash that idea if you tried: When the apple does finally break off from the branch, that elastic potential is recovered in the branch (it moves about in something like damped harmonic motion for a short while). Meanwhile, the gravitational potential energy is still available and the apple will soon convert this to kinetic energy as it falls. You could go a bit further than this if you needed to: Stop the apple falling (by holding it up with a stick for a while or something), just wait for the branch to stop waving about. Now let the apple fall. The apple seems to gain kinetic energy as usual (from what would have been described as gravitational potential) and the tree shows no changes as the apple falls. You could fit stress gauges into the tree if you wanted to. Wherever the apple is getting it's kinetic energy from, it doesn't seem to be stored in the tree or dependant on stress in the tree.
@Halc I'll reply more later and examine that link you gave. I have some annoying things to do in the real world first :(
Best Wishes and thanks for everyones time.
Post by: evan_au on 15/08/2021 03:21:31
- I was taught that it was in the separation between the apple and the surface of the Earth (although it would be greater if you had a convenient nearby deep mine shaft):
- "E=mgh"; E=Potential energy, g=gravitational acceleration, h=height above ground (or wherever it was going to end up)
- Where it was assumed that g was the same all the way down (and up)
(ii) Did you believe it? (I did while I was at school).
- Yes, although I also knew about the inverse square law for gravity.
- Assuming constant g makes the calculations easier, especially before learning how to do calculus
(iii) Was there anything different about the apple when it was up high or just that it was up high?
- Not for apples
- But for other things, like experiments where we carried weights up to the next floor and dropped them, work went into the weight to lift them up high.
- And with the traditional museum demonstration of orbits (roll a coin into a plastic "gravitational well"), the interplay between kinetic and potential energy was visible (until friction swallowed your coin... :( )
(iv) If the energy was in the apple, then did it have more mass when it was up high?
- I did not worry about that
- although I was aware of the equivalence of mass and energy.
- E=mc2 only makes a measurable difference in hydrogen fusion (at least, potentially measurable by a High School student).
(v) You may have studied more physics since school. Where do you now think the gravitational potential energy is located?
- The gravitational well of the apple merges more closely with the gravitational well of the Earth when it falls.
- The gravitational well is a map of force or potential energy (depending on the units used)
(vi) How would you go about explaining this concept to a school-age student, maybe one of your own children if you have them? Suppose they ask directly "where is the gravitational potential energy stored?" - what will you tell them?
- I like the museum gravitational well: unlike the apple, it is (partially) reversible, showing the return of kinetic energy back into potential energy.
- The total energy of the system is conserved (if you account for sound and heat).
Q: If an apple tree falls in the forest and no-one is there to hear it, does it make a noise?
A: Yes. After the event, you can see the broken branches and scattered leaves. The energy of the falling apple tree is turned into broken branches, wind which tears off the leaves, plus heat and sound.
Post by: Eternal Student on 15/08/2021 03:48:13
OK, I've looked at Halc's reference.
Looking up some reliable (reviewed) sources, we have two systems: Earth with apple on tree, and Earth with apple on ground. The proper mass of both Earth and apple is the same in both systems, but the system mass of the former (as viewed from infinity) is greater than the system mass of the latter. That implies that any meaningful potential energy location is 'the location of the system' and not the location of the apple at all.I'm surprised at you Halc. You nearly always rush to say something is only a co-ordinate effect or that something is co-ordinate dependant - but you haven't done it here. If "system mass" depends on the observer and their reference frame then why are you concerned about it? Have some faith that the best theories (like my favourite - GR) was built with tensors to be as co-ordinate independent as possible.
1. I'm not entirely sure that a "system mass" is a useful concept. It seems like an attempt to return General Relativity to a Newtonian way of thinking about gravity. They (the people on your stack-exchange site) seem to be implying that a ray of light that passes close to this earth-apple system experiences a gravitational effect (e.g. takes a curved path) that is due to this "system mass". It's OK as far as it goes, if you must think of gravity in Newtonian terms then I suppose this "system mass" is required and is definable.
Meanwhile, General Relativity is not a blunt tool - it has no need to know or care about this "system mass". The location of the apple is information that is already known and made available to the theory of General relativity. The location of the apple is encoded in the stress-energy tensor since the distribution of mass has changed slightly if the apple is on the tree or on the ground. Just change the stress-energy tensor by inputting the new distribution of mass-energy. Then "turn the handle" on the machinery of General relativity and it will correctly tell you about the path taken by light as it passes close to the earth. It will be (ever so slightly) different when the apple is located in the tree rather than on the ground. You cannot and indeed must not input any extra mass anywhere - just change the distribution (location) of the masses. Any attempt to input some extra mass because the apple was up high in the tree will break the validity of your stress-energy tensor.
This may be worth phrasing another way... see item 2. below.
2. Conceptually, General Relativity is not a strap-on addition for Newtonian gravity, rather it is a total replacement of the Newtonian theory.
You have no model of gravity until AFTER the stress-energy tensor has been calculated and then the Einstein Field Equations can be applied. Therefore, you have no way of calculating gravitational anything (e.g. gravitational potential energy) until after the stress-energy tensor has been determined. Einstein was kind enough to make sure that gravitational potential energy was not a form of mass-energy that needed to be included in the stress energy tensor. Yes, it was likely that the distance between two masses would be important or more generally the spatial distribution of mass would be important but that information was directly captured by the stress-energy tensor.
[gravitational potential energy is not needed in the stress energy tensor ---> this is close to suggesting gravitational potential energy is fundamentally not required but I'll leave that for another day and another post].
- - - - - - -
I'm over-running again and should stop talking. I'm sorry for not liking your peer-reviewed information sources about system mass. It also looks like someone else has added a post and I'm interested to see what they learnt about gravitational potential energy.
Best Wishes.
Post by: Eternal Student on 15/08/2021 11:30:22
Thanks for your reply.
I was taught that it was in the separation between the apple and the surface of the EarthThat is interesting. The gravitational potential energy wasn't said to be in or any object and/or it wasn't implied that the gravitational potential energy was possessed by an object in some way.
The next section almost contradicts this:
Was there anything different about the apple when it was up high or just that it was up high?
- Not for apples
- But for other things, like experiments where we carried weights up to the next floor and dropped them, work went into the weight to lift them up high.
Force was applied at the object and this was moved through some distance. I think everyone would agree that work was done at the object's location. If I've understood what you've said then it seems the teacher presented the common view that this work (or energy) went into the object.
So the teacher gave you two different possible locations for the energy and everyone just went along with that? It was put into the weight (I'm going to call this "the object") you carried up one flight of stairs but it was stored in the space (the separation) for the apple. For example, they could have said that work was being done against the gravitational field and implied that the energy was being stored in the field or in the separation between the object and the floor as you progressed - but they didn't do that - they implied the work went into the object.
- - - - - -
Stopped, sorry I have to do some tasks for an elderly relative. I'll write more later and I need to re-read the section about the gravity-well merging idea. Bye for now.
Post by: alancalverd on 15/08/2021 11:45:04
Likewise Newton's apple tree was infinitely stiff so didn't bend as the apple grew.
Sorry to play the grumpy engineer in this, but you may recall one of the problems of laying undersea cables or dropping hydrophones to great depth is that you can't ignore the weight of the cable - it stretches as you drop it and whilst you can ignore the elastic energy of a fly fishing line, a deep trawl cable contains a lethal load of joules.
Post by: Eternal Student on 15/08/2021 21:47:45
Where do you now think the gravitational potential energy is located?This is an unusual and somewhat oblique description of where you now think gravitational potential energy is located. It seems that you only loosely associate a location to gravitational potential. The well is a map of potential and this is important. I think you're implying that the potential is in the field somehow and spread out in space a little but mainly centred around each object. (You could be suggesting that location just doesn't matter but I've discussed that later in this post).
- The gravitational well of the apple merges more closely with the gravitational well of the Earth when it falls.
- The gravitational well is a map of force or potential energy (depending on the units used)
You seem to have thought about gravitational potential in every way here Evan_au (that's obviosuly good).
1. It could be in the field, or in the space between objects.
2. It could be in the object.
3. It's location may not matter. It's just a store of energy.
- - - - - - - -
How would you go about explaining this concept to a school-age student, ......
- The total energy of the system is conserved (if you account for sound and heat).
Well I agree that this is important and it's got to be taught to school-age children. It's also on most examination syllabuses so there really isn't a choice about teahing this.
It also links with comments and ideas presented by many physicists.
Energy could be just a book-keeping tool. It doesn't represent anything real or tangible in the universe and it does not have to be located at a definite position in space. It just so happens that in all the best theories (Newtonian Mechanics, Quantum Mechanics, Special Relativity etc.) there is some quantity which can be identified and it seems to be conserved.
It is important to realize that in physics today, we have no knowledge of what energy is. - From The Feynman lectures, vol. I Chapt. 4, circa. 1963. (To put that quote in context - Feynman went on to say that the conservation of energy is just about all we do know about energy).
Please note that I don't agree with everything that was just said, I'm just sumarising one view about energy as a book-keeping tool or abstract quantity only.
- - - - - -
In Britain, schools have been changing the way they teach about Energy in physics over the last 10 years. We are not encouraged to suggest that energy has different forms. Instead the approach of suggesting that energy is just a book-keeping tool should be used. You don't talk about "transforming" energy anymore. Instead you just identify different stores of energy (but sometimes you just can't say where exactly the store is physically located - e.g. gravitational potential energy) and then talk about transferring this energy from one store to another. It may seem like just a change of terminology but it isn't. There is the suggestion that we have incredibly little understanding of energy and it's fundamentally wrong to suggest that it exists as a real thing like a "form of energy" in our universe. Instead our understanding should be based on the principle of conservation of energy, i.e. that energy is just an abstract quantity that is conserved in all physical changes and in all models of science.
Anyway, why does this matter to me (and hopefully other people)? It's because one of my younger children is caught in the midddle of this transition over how energy is taught in school. They have one older teacher who is still pushing the old teaching method with forms and transforming and another going down the new route with stores and transferring. Meanwhile, I need to unpick and unscramble what often seems like junk that they come home with while trying not to say anything myself that would directly contradict what the new teaching method suggests.
@alancalverd ---> I appreciate that school was a long time ago and it's not all that important what was done back in the day BUT I am stuck in this sitation where I do have to re-enagage with the way things are presented in school.
How are they teaching about energy in schools in your area (country) these days? Do you know? Forms of energy and Transforming OR Stores and Transferring OR something else?
Best Wishes.
Post by: Eternal Student on 15/08/2021 22:08:41
Does an ideal fluid have a PE density?Sorry, Halc, I just spotted this and realised it could have been a question you wanted to discuss.
The use (or rather the lack of use) of gravitatonal potential energy when constructing the stress-energy tensor for General relativity was discussed in reply #9.
Obviously you can say something else or even start a new thread if you want more discussion (but you're a mdoerator and you know this better than I do).
Best Wishes.
Post by: evan_au on 15/08/2021 22:57:06
Quote from: EternalStudent
So the teacher gave you two different possible locations for the energy and everyone just went along with that? It was put into the weight (I'm going to call this "the object") you carried up one flight of stairs but it was stored in the space (the separation) for the apple.I didn't see it as different or contradictory until I saw some of the discussion in this thread.
I never studied tensors at university, so I didn't have to think much about "the energy density of a point in space" - or in this case "the energy density of a path in space".
For a pre-calculus high school student, it's easiest to calculate the potential energy based on the difference in height before and after dropping the object, and ignore everything in between (but definitely clear the area of newbies before starting the experiment!).
With calculus, you could consider a force being applied to the object over a certain distance as you lug it up the stairs, which produces exactly the same answer as you get before calculus. I expended that energy over a certain distance, but I after I have passed, you can't actually see the energy in the zig-zag pattern as I trekked up the stairs (unless you have a sensitive infra-red camera or some such..). However, if you can see a 1kg lump of iron sitting on the balcony of the building, you can see the separation, and easily calculate the potential energy.
So, whether you call it a form of energy, or a store of energy, it is easier to see where it is now, rather than work out how it got there, especially for pre-calculus students.
Changing terminology can be a pain, and using the wrong terminology can cause lose you marks in the exam. Maybe just show your child how the two systems are equivalent (for a pre-calculus student, or an examiner assuming the student is pre-calculus). Encourage the student to use the terminology that the examiner is expecting.
I frequently find myself on the wrong side of a terminology change around mass, rest mass and relativistic mass.... The answers are the same, but the terminology has changed :(
Post by: alancalverd on 15/08/2021 23:44:11
Meanwhile here's my own twopennorth. As Feynman probably said it first, you can call it two cents' worth.
Mass and velocity are intuitively obvious. A weighs more than B, cars go faster than buses. Now multiply some numbers together and define acceleration, and you have all you need to analyse and predict classical mechanics.
Energy should always and only be taught as "a conserved scalar", along with momentum as "a conserved vector". If you like, just call them "conserved quantities" and just note that momentum involves both speed and direction. This is entirely sufficient for all newtonian mechanics and stresses the importance of conservation when analysing any physical event.
This approach makes sense of gravitational acceleration, ballistics, and all the other idealised mechanical interactions including pendulums. The mechanical equivalent of heat is fun to demonstrate, as is the use of electrical energy, and you can start asking the "engineering" questions about frictional losses or transducer heating if you always assume conservation.
A skeptical note. A teacher is someone who understands something and phrases it so a pupil can understand it. An educationalist is someone who thinks he knows something and phrases it so nobody can understand it. Storage and transformation of energy seems like the language of the latter.
Post by: Eternal Student on 16/08/2021 00:53:02
Changing terminology can be a pain, and using the wrong terminology can cause lose you marks in the exam. Maybe just show your child how the two systems are equivalent (for a pre-calculus student, or an examiner assuming the student is pre-calculus). Encourage the student to use the terminology that the examiner is expecting.I'm not sure it is just terminology. Let's take this question as a simple example:
What is energy? If you were walking down the street and found something, how would you know it was energy?
Possible answers (under the old system): Energy exists in only certain forms. Just run a test for each of those forms. Is it sound energy? Is it a source of electrical energy ? etc. etc.
(Under the new system): There is no easy way to know or describe what energy is. The only way to know that what you have found is energy is to observe the ability to use it to transfer value to a known store of energy. Sadly, even if you can't transfer value to a known store of energy it doesn't show that this thing is definitely not energy - just that you haven't found a way to transfer it to another store yet.
(Ignore the system being taught in school and just free-style the answer): The usual definition of energy is something like this:
Scientists define energy as the ability to do work - taken from U.S. Energy Information Administration website.
So the typical example of an energy source is a really hot thing (like burning coals in a power station). This has a high temperature or a lot of internal kinetic energy. As the energy flows out of the hot thing into the surrouding environment, we can extract useful work. So that's OK, our definition works - energy is the ability to do work and we can say that the coal has a high energy content.
Now, you probably realise that our ability to extract useful work actually depended on temperature differences and the concepts of heat flow as described by thermodynamics. Let's assume that global warming has become such an issue that our surrounding environment is at hot as the burning coals anyway. Now we can't extract any useful work from the burning coals. Has the energy gone? Is there no energy in coal any more? Also what about really cold stuff? We can quickly reverse the engineering in our power station. Replace the burning coals with some really cold thing you brought in from our solar system. Now the heat will flow out of the environment into the cold thing and we can extract useful work while that is hapening. So the cold thing now seems to have a high energy content - we have the ability to do a lot of useful work with it. Do cold things have a higher energy content than warm things? Do things change their energy content when you change their environment? Is it better to say that energy was never an intrinsic property of the thing to begin with?
Perhaps the entire language or nature of the original question is a problem: Maybe energy isn't a physical thing you can find as you walk down the street. Energy is abstract and does not exist as a thing in the universe, there just are some stores of it. The only thing that you can find as you walk down the street is an "outlet" or an "intake" for these stores. You can find a thing with which you can interact to access a certain store of energy. This may be a lump of coal you can burn or an object with mass that you can lift up. However it is just an intake or outlet for a store, the energy was never IN the object? I don't know - just throwing out some discussion for a quiet evening. I reckon we ought to think about things like this since you're going to end up teaching it to someone. In your case (Evan_au) you have readers on this forum and you're a moderator, you could be teaching this to someone tomorrow.
------
OK, I've probably talked enough and this isn't really the chat section of the forum. Thanks for your time and best wishes to you.
Post by: Eternal Student on 16/08/2021 01:25:50
Thanks for your time and effort @alancalverd
You do know that you can slow down and do something else with your time. Also let's get some basic admin covered: This discussion may be becoming more like general chat and I have no objection to any moderator moving the thread.
A skeptical note. A teacher is someone who understands something and phrases it so a pupil can understand it. An educationalist is someone who thinks he knows something and phrases it so nobody can understand it. Storage and transformation of energy seems like the language of the latter.I agree. Sadly, teachers also have to follow a school syllabus. I'm suspicious that physics teaching will revert back to something more like the old system but in the meantime it's an awkward marriage of government recommendations and multiple teacher preferences.
Also, we've got to be open minded. We (the collective group of all scientists) have been telling certain things to pupils for years and some of them are being challenged by modern science and not just educationalists.
(For examples - see threads where Noether's theorem is mentioned and conservation of energy may not apply; threads discussing Cosmology; or the awkward truth about thermodynamics you've always known where "the ability to do work" should really be a description only of Free Energy and not a definition of "Energy" as it often used).
Best Wishes.
Post by: alancalverd on 16/08/2021 07:42:26
This may be a lump of coal you can burn or an object with mass that you can lift up. However it is just an intake or outlet for a store, the energy was never IN the object?This shows the inadequacy of energy being "stored in the object"! You can't squeeze or shake heat out of a lump of coal, nor can you burn it in an atmosphere of nitrogen. When you think about the origin of coal, it is obviously a tree that has had all the life squeezed out of it, so is in almost the lowest energy state of elemental carbon (I don't advocate igniting diamonds to measure the difference).
What you can say is that the tree used solar energy to convert carbon dioxide and water into useful structural materials and oxygen, then geological energy extracted various gases and left us with a lump of carbon which we can return to its oxide with the release of heat energy. It happens that the oxidation of carbon always involves the release of the same amount of energy as is required in the reduction of carbon dioxide. The intermediate chemical processes are very complicated, particularly in the forward direction (photosynthesis generates PhD theses by the score) but the physics is straightforward (energy is conserved in every interaction) so provides us with a trail of breadcrumbs through the chemistry and the means by which I can follow biochemistry research presentations!
Post by: evan_au on 16/08/2021 10:07:47
Quote from: Eternal Student
Replace the burning coals with some really cold thing you brought in from our solar system. ... Do cold things have a higher energy content than warm things? Do things change their energy content when you change their environment?For the last question: Yes.
- If you take an object to the building balcony, it has a certain amount of potential energy.
- Now, if you build up a mound of dirt to the same height as the balcony, there is effectively no potential energy (the separation drops to zero). The potential energy changes when you change the environment
- Now, mound the dirt even higher, and it will consume energy to get it off the balcony (the separation becomes negative)
- So it is fair to say that you measure energy content relative to some reference level
Thermodynamics has some similarities:
- If two bodies have the same temperature & pressure, you can't extract useful energy - the potential energy in this closed system is zero
- The special case for thermal energy (as developed by Carnot) is that there is a limit to the amount of energy you can extract, and the extractable fraction increases with the difference in temperature.
- The fraction is also better with an "infinite" heat sink (ie able to absorb all the heat from the hot body, without a detectable change in temperature)
There is a somewhat similar situation with electrical charges.
- You can't extract electrical energy from two objects at the same voltage
- The extractable energy increases with the difference in voltage
- The extractable energy is also better with an "infinite" current sink: "Earthed" (ie able to absorb all the current from the charged body, without a detectable change in voltage)
Post by: TommyJ on 16/08/2021 12:21:01
"the ability to do work" should really be a description only of Free EnergySchool variant.
If a body or several interacting bodies (a system of bodies) can do work, it is said that they have energy.
Potential energy is called energy, which is determined by the mutual position of interacting bodies or parts of the same body.
'Hotter and colder' are rather relative notions. 'Hotter has more hot energy'.
And same about charges.
When we talk about energy of a system, which work was done to put the system into the state is not mentioned.
Post by: yor_on on 16/08/2021 15:56:46
That one is something you actually need to clarify :)
And don't you try to avoid it.
I always questioned the idea of potential energy. It irritates me.
Post by: alancalverd on 16/08/2021 17:03:10
Objects accelerate when subject to a force.
Suppose a given object has a property called mass, m. By experiment (altering m or F) we can see that F = ma.
We see the apple accelerate so there must be a force attracting the apple to the planet.
Since the gravitational acceleration of all small objects (i.e. mobj << m planet) is the same*, the gravitational force must be proportional to the mass of the object. We can demonstrate this with a beam balance. Call the constant of proportionality g, with the dimensions of acceleration.
Now define work as force x distance moved. If we lift the apple with force mg through a height h, we have done work = mgh.
Experimentally we find that the apple reaches a speed v when dropped such that gh = ½v2. This should come as no surprise dimensionally because g is after all an acceleration. The interesting point is that something seems to be conserved: by experiment, gh = ½v2 for all values of h.
Now m hasn't changed, so the work we put in, mgh, has the same value as ½mv2. For convenience, to distinguish between the conserved quantity before and after the apple falls, we call them potential (because it hasn't started falling yet) and kinetic (i.e. moving) energy.
If you want to move away from Newton's apple (m<<M, r <<R) you can look at Cavendish's experiment which showed that for commensurate values of m and M, the attractive force between objects is actually F = GmM/r2. And now we are talking about gravitational fields (ah, the beloved inverse square law!) rather than an empirical observation.
*a good point at which to raise Galileo's thought experiment: what happens if we glue the little rock to the big rock? Does the little one slow down the big one, or does the big one speed up the little one? Either statement contradicts the other, so g must be constant for all objects.
Post by: yor_on on 16/08/2021 17:59:00
In all 'free falls' gravity is non existent, locally defined. I've seen is treated as 'field' of 'energy' but 'energy' is just a coin of exchange. you can state is as the apple falls to earth due to gravity, you can also state it as earth accelerating towards the apple or as both, as a sort of 'system', are acting upon each other.
I'm guessing ES refers to the stress energy tensor there? And possibly treating gravity as a field?
=
eh, well, looking again, that is what it says :) the quote I took from him.
This one is also about 'energy'
http://www.preposterousuniverse.com/blog/2010/02/22/energy-is-not-conserved/
Post by: yor_on on 16/08/2021 18:19:18
What molasses, and what happens when you become weightless? Doesn't motion change it? Relative or accelerating.
=
'Real' accelerations differs from a gravitational in that you will notice yourself gaining a 'gravity' locally defined. A gravitational acceleration becomes the opposite, you gain no mass from it, instead you become 'weightless' . All locally defined.
(as per Einsteins equivalence principle, the original one)
spelling
=
potential energy is overall a very tricky subject in that, the way I see it, you can define yourself to have a infinite amount of simultaneous 'potential energies' just as you can define yourself to have a infinite amount of time dilations, or speeds, just by defining it relative something else.
Post by: Eternal Student on 17/08/2021 01:49:43
This thread has been busy with several people posting. I hope everyone is well and thank you all for spending some time.
@evan_au
I quite like and agree with with most (possibly all) of what you've said. The main thing is that you're thinking about (and making me think about) energy and some of the problems we have understanding it.
One of the things you didn't mention at all was that just changing reference frames can change the kinetic energy you would associate with an object even in the most simple Newtonian system.
- - - - - - - - -
@TommyJ
That's also quite good and quite interesting.
Potential energy is called energy, which is determined by the mutual position of interacting bodies or parts of the same body.That's OK for most uses of the term "potential energy" that school age pupils may encounter. However, they also encounter terms like "chemical potential energy".
- - - - - - - - -
@yor_on
It's very kind of you to state that you are interested in hearing more. I might talk a bit more about gravitational potential energy but this forum (and especially this section) isn't my personal website or "Blog". I'm trying not to lecture or preach here. I think forums work better when there is discussion between people and that's what I was hoping to get here.
It also takes hours to write something carefully, accurately, use Mathematical notatation in it and correctly identify references to back up some issues. To be honest it's taken me hours just to write this post because I wasn't at all sure what I was going to say and how best to say it.
Finally, please remember that I learnt General Relativity from a book. I'm not an expert in very much. With this in mind, I'll try and comment on what you've written but it's not like my opinion matters a lot, it's just all I can offer.
..I have some different ideas. One of them is that a gravitational acceleration is coordinate dependent, as I understand it defined in relativity. Or as Pete used to describe it, by changing coordinate system you can 'transform away' gravity. Locally non-existent, 'globally' as from another coordinate system existing.This is mostly OK. There is some need to keep Newtonian definitions of "gravity" seperate from G.R. definitions of "gravity". In Newtonian theory, "gravity" is a force. In GR "gravity" is a curvature in a manifold. You have blended the two theories together when you started talking about a "gravitatonal acceleration" and then ended the sentence with "as I understand it defined by relativity". You don't need relativity to remove acceleration by choosing the right co-ordinates. However, you can almost get away with blending these two theories in this case because of something very special that happens...
1. When you said "gravitational acceleration" is co-ordinate dependent it's better to state that any acceleration (regardless of what you think caused it) is co-ordinate dependant. So we can find co-ordinates in which this acceleration is 0. This doesn't require anything more complicated than Newtonian mechanics.
2. The second half of your sentence is based on the idea that we can find co-ordinates (the LIF or Local Inertial Frame) so that every manifold behaves like the flat Minkowski manifold (although only in a small region). Newton didn't really care about Riemann manifolds, why would you want to find co-ordinates so that this nonsense happens? It doesn't seem related to anything useful.
3. The amazing thing is that, if you construct the appropriate manifold, then in the right co-ordinates (the LIF) both these things (1) and (2) happen at once. The acceleration required in the Newtonian theory drops to 0 and also the manifold behaves like the the flat Minkowski manifold. This is one of the things that suggested to Einstein that gravity could be modelled as curvature in a Riemannian manifold.
Now, as a consequence of this it is possible to state that "we can remove gravity" by choosing certain co-ordinates and it doesn't matter how you are defining "gravity". We can use the Newtonian concept of gravity as an acceleration OR the GR concept of gravity as curvature.
You have qualfified (restricted) the statement adequately by stating that this only holds "locally".
I'm guessing ES refers to the stress energy tensor there? And possibly treating gravity as a field?Maybe. Although I think there's two different fields we might be talking about here.
1. GR can be considered as a reasonably self-contained field theory all on its own. This is a classical field theory not a quantum theory and "the field" of interest here will be "the metric field".
2. It's also possible to consider gravity as one of the fundamental fields in Quantum Field Theory and then the field of interest here will be "the graviton field". * [Late editing: Note that Gravitons have not been discovered and QFT is not a fully comprehensive quantum theory of gravity. In particlular QFT within a framework of curved spacetime would be something different again].
The metric field is not the same as the graviton field, they are from two separate theories. Some of the more recent posts in other threads have been talking about Q.F.T. and some have been talking about the metric field and classical General Relativity. I know more about Classical GR rather than QFT. Personally, I think the metric field is a fundamental field that exists in space - but I use the word "fundamental" only in the ordinary way. It is basic, essential and naturally inherent in space. In particular it describes the geometry of spacetime.
Other people reserve the word "fundamental" to refer to the fundamental forces and/or fundamental particles in Physics and then a fundamental field is one that models those particles - so they would consider fundamental fields to be those fields used in QFT. I think some of your ideas about a description of gravity as a field of energy originate from some articles about QFT you may have read. I'm not sure that I can help much with QFT (sorry).
@alancalverd Thanks for your recent post.
For convenience, to distinguish between the conserved quantity before and after the apple falls, we call them potential (because it hasn't started falling yet) and kinetic (i.e. moving) energy.I think this is very much how the subject was originally developed (the real historical development). It's good in that it just directly presents what we observe and why we would start to think that terms like potential energy are useful. Indeed, they are useful in simple systems modeled with Newtonian mechanics but their origins were purely mathematical - there was a quantity that seemed to be conserved, we gave it a name and some years later, more meaning or importance has been attached to this concept then it deserved. You know you are almost suggesting that the entire law of conservation of energy should be presented differently to children: "We speculate that energy can be usefully defined in every system and we speculate further that this will be conserved BUT it's mainly an extrapolation based on something that we knew for a small number of special cases".
Personally, I'd be happy to present that version of the law of conservation of energy to children.
Best Wishes.
Post by: alancalverd on 17/08/2021 08:47:57
He had two apples, one about twice the diameter of the other.
He dropped them both at the same time and noticed that they hit the ground at the same time.
Even without reading the student laboratory guide, he repeated the experiment.
Having obtained the same result, he changed hands and did it again.
Satisfied that h = kv2 {∀ m,h} , he ate the apples.
So how come the National Curriculum still makes a pig's ear out of it?
Post by: TommyJ on 17/08/2021 08:59:53
gorilla in Chessington Zoo discoverIt didn't articulate it to others.)
Post by: alancalverd on 17/08/2021 10:36:55
Obviously gorillas teach their young and communicate about things that matter to the family. It will be interesting to see whether they do indeed discuss mathematical abstractions at GCSE level - it's clearly beyond the ability of most humans.
Post by: alancalverd on 17/08/2021 10:38:07
It didn't articulate it to others.)...and wouldn't have been burned at the stake or forced to recant if he had.
Post by: Eternal Student on 17/08/2021 11:05:43
About the National Curriculum ---> Obviously it's nasty thing but we should also mention one positive thing about it.
It's an "entitlement curriculum". Pupils are protected from the bias of teachers to some extent.
For example, a Biology teacher must teach the children about Darwinian evolution. They can also talk about something else if they wish but Darwin must be there and it should be clear to the pupils that this is what they will be examined on. In the same way, we can (and probably should) spend some time talking about our own understanding of energy and interpretations of the conservation of energy BUT the pupils are protected from outrageous whimsy and corruption to some extent.
Even where the National Curriculum just gets things plain wrong - at least later institutions have a reference standard to use. They know that this piece of junk is what the pupils will be coming in with, regardless of which village community they were taught in.
Best Wishes.
Post by: yor_on on 17/08/2021 11:47:35
Yes, a lot of things discussed. and I will have to go through them all methinks :) I will assume that you by using the 'metric field' refer to the geometry of SpaceTime? And I don't think I will discuss it in form of QFT, aka, gravitons. I find them quite questionable myself.
Post by: yor_on on 17/08/2021 11:50:07
=
Which btw makes your definition of it as a metric field very acceptable to me. You could say that me wondering about a Higgs field, and the way it is supposed to give particles mass, versus, the way relativity differs between accelerations, giving you a gravity, aka a added mass on a scale, and 'relative motion' comes in as part of that.
It's about the reality of nature. Is it 'grains' creating it, or are those 'grains' just a result of something else. A perfect example is lights duality.
Post by: TommyJ on 17/08/2021 12:17:32
While I was my the last years at school, I had to study physics deeply with PhD. Technical mentor additionally. And somehow he managed to put the knowledge within consumable time and level.
It is not trivial to explain to a school student not only physics, electrodynamics .. literature. To transform it to the limited math and understanding.
Some professors tell to university newcomers: 'Forget everything that you were taught at school'.
Post by: Colin2B on 17/08/2021 12:21:26
It did demonstrate the principle however. A good student watching could learn something :Dgorilla in Chessington Zoo discoverIt didn't articulate it to others.)
Post by: yor_on on 17/08/2021 12:51:22
They doesn't, I've seen it used describing stress energy tensors. It seems to come from that formula used to describe the equivalence between mass and energy. Then stretched to 'gravitational fields' and the 'energy' they contain.
=
I also remember Pete looking at in much a similar way. I don't know to what degree he had studied Relativity, but I found him quite proficient in it .And the way he looked at mass, all included, was in form of 'energy'. And I think he used it also to describe those 'fields' from. Forms of 'energy'. Myself I don't know, if we use the metric of SpaceTime then it exist, and it's also observer dependant. I use to differ between a abstract 'global' definition of the universe, versus a local definition. From the abstract we all have a 'same universe', the same metric. Locally I don't see it as we do, speeds, accelerations and its equivalence, mass. F.ex, using a extreme, what is the metric of a 'photons' propagation through our abstract definition of a universe. Does it exist, and if so, from whose definition?
( I agree to the difference there between dependent and dependant btw, thanks for that one ES, will blame that on my lack of knowing enough nuances in english. Always something new to learn :)
It can become very tricky if one wants to define it through the universe containing a 'energy'
Just read this http://www.preposterousuniverse.com/blog/2010/02/22/energy-is-not-conserved/
He uses a redshift of light as one example. And states that it proves that 'energy is not conserved'. And we might assume that this means that light must 'propagate'. But I don't think it necessarily needs to be so. We could just as easily refer to it as laws and properties defining it without using a propagation. It gives us a logic any which way. Just as using a duality does, without locking it to neither waves nor 'photons'. So I'm of two minds when it comes to fields, but I do know that the 'metric of SpaceTime' exist, with or without it being a 'field of energy'.
And yes, assuming laws and properties to define it instead of a propagation makes it possible to define it as 'energy' is conserved, 'globally' defined. Well. as I think of it for the moment.
You can turn it around also and then define all energy as different types of 'mass'. That would probably suit those looking for 'grains' more than the opposite.
I seem to remember Sabine being somewhat of a devotee of 'Super Determinism'. In that view, and as far I've looked it up, everything becomes predestined. And if it would be that way energy has to be 'conserved' from a 'global' standpoint. It can't lose anything, everything becomes 'locked up', as far as I see?
Found a link https://backreaction.blogspot.com/2019/07/the-forgotten-solution-superdeterminism.html
Post by: Eternal Student on 17/08/2021 23:24:59
I also remember Pete looking at in much a similar way.I'm sorry but I don't know Pete. I think he used the forum before my time here. I've heard from other posts that he has passed away. I'm very sorry.
What you're describing about energy and the stress-energy tensors does sound like the standard or main approach to General Relativity but I don't really know exactly what it was that Pete did or was intending to do.
There are online lecture notes from Sean Carroll that describe GR and show how all the components of the theory are defined and constructed. (This is the same person that you gave a link to in your post).
https://www.preposterousuniverse.com/spacetimeandgeometry/
I learnt about GR from the textbook written by Sean Carroll which is based on those lecture notes (but the book will cost you a lot of money, while the lecture notes are free if a little outdated).
I'm not going to re-present the theory of GR here, it would take too long and I really can't do it any better than the myriad of other courses and textbooks that are already out there. However, I'm fairly sure bits and pieces will be mentioned occasionally.
The link you gave: "Energy is not conserved" is a good article that I'm familiar with and I've recommended it to others in the past. The main point made in it is exactly as stated in the title - Energy is NOT conserved and the example is exactly as you have described. I'm glad you mentioned here because it is obviously relevant to this thread. It is certainly something that everone should read before they start telling children about the conservation of energy.
...'Super Determinism'. In that view, and as far I've looked it up, everything becomes predestined. And if it would be that way energy has to be 'conserved' from a 'global' standpoint. It can't lose anything, everything becomes 'locked up', as far as I see?The first part seems right. Super Determinism does generally imply that everything is predestined.
The second part may be true. I haven't studied Super Determinism much since it isn't one of the more popular interpretations of Quantum Mechanics. However, it seems that Super Determinism does not prevent the expansion of space and the red-shift of photons exactly as you described in your link "Energy is not conserved". So, it doesn't force energy to be conserved if we were defining energy in the same old-fashioned way (as the ability to do work). I'm sure you can define energy in a different way (some consider energy as information and information is conserved in quantum mechanical systems).
Oh yes... and I didn't have my spell check switched on. Dependent and Dependant are different but I'm not sure I did that deliberately, sorry.
- - - - - - - - -
I think it's time for another question:
How much energy does it take to make a magnet?
You've probably made a permanent magnet in school. You might have stroked a piece of iron with an existing magnet or else placed some iron between some coils of wire and passed electricity through the coils for a time.
It seems clear that some energy was used to create the permanent magnet. It's probably not much. maybe you used an electromagnet drawing 1 KW of electrical power for about 5 minutes. I don't know, something like this.
Anyway, once you've got this permanent magnet it will start attracting other bits of Iron. There's quite a lot of Iron in the universe, possibly an infinite amount. To use Evan_au's favourite way of visualizing a potential energy, there's now a magnetic potential well available and we can use this.
Ignoring friction and other inconveniences as usual, we can allow all the Iron in the universe to come to our new magnet. How much kinetic energy can we harvest at the magnet? Where did all this magnetic potential energy come from?
Best Wishes.
Post by: yor_on on 18/08/2021 08:32:51
=
You wrote " Super Determinism does not prevent the expansion of space and the red-shift of photons. " and I think it doesn't matter how the universe is expected to behave if it would be predestined. The only thing that would make it weird, to me then, would be if it behaved 'magically', aka if we could find no logic explaining it, no rules, no laws and no properties. One could of course argue that what we can't explain, as 'spin' and 'probability' in quantum mechanics are just such factors. But I would still say that a overwhelming part of the universe has a logic that we can follow. And that we find a logic in quantum mechanics too.
There might be a subtle point to that. For Creationists the universe is something 'created'. If we assume that a 'God' can do whatever he/she/it please, then logic doesn't matter for it, in a choice between what I call a magical universe or one logical . So the logic's we find existing, assuming this to be correct, does not point in a creationist direction.
Post by: Eternal Student on 18/08/2021 23:54:34
But I would still say that a overwhelming part of the universe has a logic that we can follow.Yes, I agree.
Although you could also argue that we (human beings) are just extremely good at finding patterns and very likely to forget about something that didn't make sense or follow a pattern.
You will notice that two things do seem to be related and remember it. This is useful for your survival. Meanwhile, there could have been 100 other things that were not related in any way. You won't notice or remember those.
Let's take some examples:
1. We can see a relationship between electricity and magnetism.
2. We can't see a relationship between "what you eat for breakfast" and "what the weather will be in France".
We remember 1. We forget about 2. We don't even ask the question why isn't the weather in France related to my choice of breakfast?
Post by: Eternal Student on 19/08/2021 00:02:40
How much energy does it take to make a magnet?
You've probably made a permanent magnet in school. You might have stroked a piece of iron with an existing magnet or else placed some iron between some coils of wire and passed electricity through the coils for a time.
It seems clear that some energy was used to create the permanent magnet. It's probably not much. maybe you used an electromagnet drawing 1 KW of electrical power for about 5 minutes. I don't know, something like this.
Anyway, once you've got this permanent magnet it will start attracting other bits of Iron. There's quite a lot of Iron in the universe, possibly an infinite amount. To use Evan_au's favourite way of visualizing a potential energy, there's now a magnetic potential well available and we can use this.
Ignoring friction and other inconveniences as usual, we can allow all the Iron in the universe to come to our new magnet. How much kinetic energy can we harvest at the magnet? Where did all this potential energy come from?
I'm keen to get some answers.
Best Wishes to everyone.
Post by: TommyJ on 19/08/2021 09:04:10
In a half-field shell electrons are not paired and their tiny magnets are pointing in the same direction. This is intrinsic magnetism of electrons.
But if an atom is magnetic, it doesn’t need that the material made of lots of these atoms are magnetic.
Crystals. Ferromagnetic - a bunch of atoms are aligned in the same magnetic direction. Aligned domains (bunches of bunches) of atoms. This is a quantum property - aligned to macro size.
Domains of material can point in different directions.
Piece of iron may not have a magnetic field at all, because all domains are pointing to different directions.
However if you apply a strong magnetic field from outside the material, you can make one solid unified piece of magnet.
Magnetism is a quantum property magnified to the size of the object.
These criteria are difficult to fulfill. There are few materials that can do that: Fe, Co, Ni, Gd.
Wikipedia:
The magnetization of a magnetized material is the local value of its magnetic moment per unit volume, usually denoted M, with units A/m. A good bar magnet may have a magnetic moment of magnitude 0.1 A·m2 and a volume of 1 cm3, or 1×10−6 m3, and therefore an average magnetization magnitude is 100,000 A/m. Iron can have a magnetization of around a million amperes per meter.
Post by: Eternal Student on 19/08/2021 12:11:15
Thanks for your reply TommyJ. This was mainly about why a material is magnetic but that's a perfectly sensible place to start. This section in particular is useful and something like this is usually taught at school level:
Domains of material can point in different directions.
Piece of iron may not have a magnetic field at all, because all domains are pointing to different directions.
Ferromagnetic objects are considered as a collection of little magnetic regions called domains. Every domain is a tiny magnet in its own right. When these domains are aligned then the overall piece of Iron will behave like a magnet.
With this in mind it is possible to argue that all the potential energy you require to explain what happens in reply #39 was actually always there. There was always the potential to recover kinetic energy by allowing other lumps of iron to approach any one of these domains in your magnet. The total potential energy available is then the sum of the potentials for all the domains.
To phrase this another way, the little bit of energy we put in to induce permanent magnetism in our Iron bar wasn't creating the massive store of potential energy. That store of potential energy was always there. Inducing magnetism into our Iron bar just made it possible for us to access that store.
OK, that's one argument that could be presented and (I think) might be acceptable for school-level. Anyone else have another argument?
Best Wishes.
Post by: yor_on on 19/08/2021 14:08:35
" We remember 1. We forget about 2. We don't even ask the question why isn't the weather in France related to my choice of breakfast?"
Hmmm, entanglements?
Post by: yor_on on 19/08/2021 14:12:07
Magnetism I mean.
https://www.nap.edu/read/10118/chapter/7
Post by: alancalverd on 19/08/2021 17:48:43
I tried using the analogy to teach 10-year-olds the value of tight binding in a rugby scrum but our masters at Twickenham thought I was mad and wouldn't add it to the curriculum. Don't they learn anything at primary school?
I once managed to shunt a car, just enough to magnetise it without rendering it undriveable. Made navigation easy thereafter as whatever road I took, the compass indicated "south".
Post by: Eternal Student on 19/08/2021 22:45:10
I once managed to shunt a car, just enough to magnetise it without rendering it undriveable. Made navigation easy thereafter as whatever road I took, the compass indicated "south".I'm sorry to hear this. Did you try getting the car warm and then driving into something else, or just go around the car hitting it with a small hammer?
Seriously, how did they de-magnetise the car?
Post by: alancalverd on 19/08/2021 22:52:17
Lost with a rental car but no map, I phoned my client and explained the predicament. He said "This is Ireland. Stop the car for a few minutes. The wettest window is on the west." No problem.
Post by: Eternal Student on 19/08/2021 23:01:19
Well, there is a symmetry to it?I'm not sure what you meant. Also, I only find a thing that I have to download on the website you linked to. It looks like an entire book. I was a little concerned about downloading anything since I don't recognise the site. Is it really worth downloading? Are you strongly recommending it or was it just a few sentences in the book that you could copy-and-paste into the forum directly?
Magnetism I mean.
Best Wishes.
Post by: Eternal Student on 19/08/2021 23:12:00
;D for the joke.
Lost with a rental car but no map,That reminds me, did you ever hear anything from your school Physics teacher friend? Don't worry too much if you didn't.
Post by: yor_on on 20/08/2021 09:13:06
Post by: alancalverd on 20/08/2021 13:16:38
That reminds me, did you ever hear anything from your school Physics teacher friend?Actually my son, who may join the forum but said en passant that it is indeed a bit byzantine at present.
Post by: yor_on on 21/08/2021 08:41:27
Can't help linking this one. https://hackaday.com/2016/03/21/just-when-you-thought-magnets-werent-magic-magnets-are-mechanisms/
=
Now if that is the what you're thinking of we need some history to it, well, as I think. Because the modern representation is connected to special relativity.
so first, one should read this https://en.wikipedia.org/wiki/History_of_special_relativity
And when that is done, this https://en.wikipedia.org/wiki/Classical_electromagnetism_and_special_relativity
and then this https://en.wikipedia.org/wiki/Magnetostatics
not that it make it simpler :)
=
As I dabble in physics again, we should probably add this too.
" Whether a particle is or is not elementary depends on the description level. As our knowledge about microscopic physics increases, objects once considered elementary were found to have a substructure that can be modeled on a more detailed level. Thus atoms, once thought of as elementary are today described as consisting of nuclei and electrons; nuclei are described as consisting of protons and neutrons, and the latter is thought of consisting of quarks. Whether quarks have substructure is presently unknown.
A particle is considered to be elementary (on a given description level) if it is sufficient to describe it by an irreducible unitary representation of the Poincare group or its Lie algebra. This group is dictated in QFT by the symmetries of space-time at experimental microscopic scales. The 10 independent observables of this Lie algebra are the four components of a 4-vector ##p## describing momentum, three components of a 3-vector ##J## describing angular momentum, and three components of another 3-vector ##K## describing infinitesimal boosts.
For massive particles such as the electron, one can construct from these an additional 3-vector ##q## describing the particle position in an observer-dependent frame. For massless particles such as the photon, a sensible position vector does not exist. "
https://www.physicsforums.com/insights/physics-virtual-particles/
=
Just a comment. It makes it time dependent, aka depending on ones 'frame of reference' as I see it. And to understand ones 'local frame of reference' correctly you need to see that your local 'clock' never lies, and that it will be the clock you use to define all other 'clocks' relative.
But it should also be connected to HUP, aka 'virtual particles' spontaneously creating a 'pair production' of 'real particles', under a time and energy constraint. The more 'energy' the more 'virtual particles/energy' creating those 'real particles'.
But still governed by HUP and Planck time. That one might be questionable but that is how I think about it. I can't find a link to the question if a pair production can exist over a Planck time before annihilating itself but I would expect it to be governed by the uncertainty principle.
And that should place it outside our local definitions of what's real. And so outside Plank time, except in very special circumstances as the 'Big Bang' in where it is assumed to create 'real particles'. And to do that you need something more than just a 'spontaneous pair production'. You need 'something' changing it.
So there are two aspects to it. One what I tend to call 'global', frames of reference interacting, the other one strictly local
=
While this may move it into 'New Theories' we could add that if 'time' and 'clocks' is something belonging to SpaceTime, and then add that what was before it involved no clocks, it might be one approach to defining it. You could also differ between the idea of 'time' as a law, versus the idea of 'clocks' as its property proving its existence to us.
The point there being that 'dimensions' as such isn't a preexisting factor defined this way. Instead being a result of the Big Bang and clocks coming into existence. And what it should do to our universe is to define it as a exception, a 'singularity'.
Post by: Eternal Student on 21/08/2021 16:15:08
Hi again,
Thanks for all your comments Yor_on. The scope of this thread is growing beyond anything I imagined. The links you provided are interesting but I can't respond to all of them today. I also think it will go far beyond what was originally described as a "school-level question" in my title.
So what are you thinking of ES?..... I thought you might refer to laws and properties but if it is something else it's time for you to state it, as nothing seems to fit?It probably is time to say something about what I think and perhaps explain why I don't think gravitational potential energy is required.
1. Potential energy (of any kind) is something that tends to be invented (in the sense of given a name) whenever existing forms of energy are insufficient to account for the total energy in the system.
Alancalverd presented one example of this in his/her earlier posts. For simple Newtonian systems with gravity it is noted that
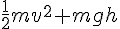= constant.and then the quantity mgh was called gravitational potential energy.
[see reply #22 and #25 on this thread for more details]
There are many examples where the term "potential energy" is introduced just because it's convenient. It represents the most abstract part of a conserved quantity that exists in some systems. Specifically, since Total Energy is conserved, we tend to sum all the forms of energy that can be seen and then subtract this from the total energy. This "bit left over" is given the name "potential energy" but it is abstract and (in my opinion) quite misleading to suggest that this potential energy is any sort of fundamental or tangible thing that exists in the universe.2. Historically, the existence of a conserved quantity that could be considered as energy was a conjecture (a generalisation or extrapolation) based on what we knew for only a small number of special cases.
3. The first mathematically rigorous proof that systems have conserved quantities which we could call Total Energy (and also momentum and angular momentum) was provided by Noether's theorem circa. 1918. This assumes that a "system" can be described by a Lagrangian and a least action principle governs the evolution of the system. I am not aware of any proof that all things we might want to consider as a physical system can be formulated in this way (with a Lagrangian). However, many of them can and it is now so widely accepted that this is the correct way to model physical systems that we will just go along with the idea that all physical systems can be described with a suitable Lagrangian for the remainder of this post.
Noether's theorem showed that symmetries were required in the physics of the system to produce these conserved quantities. There is a correspondence between the symmetries and the conserved quantities. Given a symmetry we can find a conserved quantity but also we can reverse this - given a conserved quantity we can find a symmetry that the Lagrangian must obey.
This is all inherently abstract mathematics. It describes energy as a mathematical expression involving several canonical variables that were sufficient to describe the Lagrangian of the system. These expressions for Energy don't always break apart into easily identified components. It is just a relationship between some canonical variables that are unique to the individual system.
In particular, Noether's theorem does nothing to identify fundamental forms of energy that may exist in the universe. In many systems there isn't a quantity that looks like or behaves like gravitational potential energy. Furthermore, Noether's theorem does not define energy as the "ability to do work", it is just an abstract relation between some variables.
4. Our best theory of gravity is still General Relativity (but I'm biased because I like it). In this, it is important to identify all sources of energy-momentum since this will be the source of gravitation. In particular, the energy density due to the content of the manifold must be specified.
(i) You are not required to include gravitational potential energy as a form of energy-momentum that contributes to the stress-energy tensor. (This was discussed in an earlier reply).
(ii) You are not able to include gravitational potential energy as a source of mass-energy even if you wanted to. Some of this was also discussed in earlier replies. There is a problem knowing where in space this energy would be located (for example, is it in the earth or in the apple, or spread out in the space between them). You don't actually have a working model of gravity as described by GR yet so any method of calculating gravitational potential energy would need to be based on some other theory available to you - such as Newtonian gravity. There is also a problem trying to determine how much gravitational potential energy there would be due to each particle in your system. For example, if you were using Newtonian gravity to calculate the potential energy then you have this formula to work with:
Gravitational potential energy =
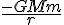so that grav. p.e. → ∞ as r→0.We can then place two particles of matter close together and provide arbitrarily large (large negative) energies. If we assume that this energy is located in the vicinity of those particles then strange things would happen. It would make two small particles of mass m that were close together the single most important source of gravitation in the manifold, far more important than say one particle located further away with a mass of 1000m. Now, it seems that this is not what happens in reality. Newtonian gravity describes the situation well enough for most purposes. If we put a test mass half-way between the 1000m mass particle and the pair of smaller particles of mass m that are close together, then the pair of close particles just behave like one particle of mass 2m. The test particle is not attracted to the close pair of small particles, instead it is pulled toward the more massive 1000m particle. Just in case you were concerned that the energy is a large but negative in the vicinity of the two close particles, the test mass isn't repelled by those two close particles either - it just sees them like one particle of mass 2m.
We have already discussed the idea that gravitational potential energy should NOT be included as a contribution to the stress-energy tensor but this makes gravitational p.e. stand out from all other forms of energy. In the theory of GR all forms of energy are sources of energy-momentum for the stress-energy tensor and we've got to ask why gravitational p.e. wouldn't be included - perhaps it is not a fundamental form of energy after all.
Another reasonable possibility is that if gravitational potential energy exists and should be included as a source of energy-momentum for the stress-energy tensor then it is not localised in or around two objects that are a certain distance apart. Instead that energy is spread uniformly throughtout the manifold. We already acknowledge that we cannot measure the absolute value of most forms of energy that contribute to the stress-energy tensor. The electric and magnetic fields are a common example since day-to-day physics only involves the differences between these potentials not the absolute value of those potentials. Anyway, if gravitational potential energy is a form of energy that is spread uniformly throughout the manifold then it would seem to be a component of the vaccum energy.
OK, I've over-run my time here again. Let's just say that I don't think gravitational potential energy is required, we already have vaccum energy in GR.
(iii) Finally, I should mention that, unlike the Newtonian theory of gravity, gravitational potential energy does not emerge as well defined quantity after GR. There are some situations where time-like Killing vectors can be identified and symmetry conditions like those required in Noether's theorem are met - but there are many situations where this can not be done.
In general relativity gravitational energy is extremely complex, and there is no single agreed upon definition of the concept. It is sometimes modelled via the Landau–Lifshitz pseudotensor....
[Taken from Wikipedia https://en.wikipedia.org/wiki/Gravitational_energy#General_relativity]
Summary
1. Energy is an extremely complicated thing.
2. Gravitational potential energy is more likely to be an emergent property. Some systems have an abstract relation between some variables that we can identify as and call gravitational potential energy but this is a property of that system. Gravitational potential energy is unlikely to be a fundamental form of energy that exists in the universe.
3. If we step back and re-examine something that @Halc mentioned in reply #5 we can start to make sense of it another way. If we consider a system that is the earth with all it's apples on the trees compared to a system which is earth with all it's apples on the ground, then we can attempt to consider how much force would need to be applied to these entire systems in order to start to move them. The system with the apples on the trees, has a slightly higher inertial mass then the system with all the apples on the ground. So the increased potential energy of the system seems to show up as a change in inertial mass of the system. This is one interpretation for the quantity Halc described as "system mass". It's perfectly sensible but only required because we were considering the earth-and-apples system as if they were one combined particle. If we take a suitable reductionist approach to analysing these systems then gravitational potential energy is not there to be found and indeed neither the earth nor the apples have changed their mass at all just because their positions have changed.
4. I only started the thread to discuss some basic science that we start teaching children at school and mainly just to pass a few evenings in discussion. If the thread has made anyone pause to reconsider what they thought they knew about Energy and how they should present to children then that'll be a bonus.
Thanks to everyone who has spent some time here. You are all free to continue commenting of course and indeed you can rip apart anything I've said apart if you want to.
Best Wishes.
Post by: AJ_WWE on 31/12/2022 16:40:53
‘How to be a magnet’. It depends on the size of ferromagnetic and it’s crystal domain alignment.
In a half-field shell electrons are not paired and their tiny magnets are pointing in the same direction. This is intrinsic magnetism of electrons.
But if an atom is magnetic, it doesn’t need that the material made of lots of these atoms are magnetic.
Crystals. Ferromagnetic - a bunch of atoms are aligned in the same magnetic direction. Aligned domains (bunches of bunches) of atoms. This is a quantum property - aligned to macro size.
Domains of material can point in different directions.
Piece of iron may not have a magnetic field at all, because all domains are pointing to different directions.
However if you apply a strong magnetic field from outside the material, you can make one solid unified piece of magnet.
Magnetism is a quantum property magnified to the size of the object.
These criteria are difficult to fulfill. There are few materials that can do that: Fe, Co, Ni, Gd.
Wikipedia:
The magnetization of a magnetized material is the local value of its magnetic moment per unit volume, usually denoted M, with units A/m. A good bar magnet may have a magnetic moment of magnitude 0.1 A·m2 and a volume of 1 cm3, or 1×10−6 m3, and therefore an average magnetization magnitude is 100,000 A/m. Iron can have a magnetization of around a million amperes per meter.
Thanks for the link. But this rule does not always work. In our university laboratory, we used a press to draw stainless steel. After this process, part of the material was magnetized, and part was not. I can not understand how the material properties could change so much.
Post by: JimmyW9 on 31/12/2022 16:43:57
‘How to be a magnet’. It depends on the size of ferromagnetic and it’s crystal domain alignment.
In a half-field shell electrons are not paired and their tiny magnets are pointing in the same direction. This is intrinsic magnetism of electrons.
But if an atom is magnetic, it doesn’t need that the material made of lots of these atoms are magnetic.
Crystals. Ferromagnetic - a bunch of atoms are aligned in the same magnetic direction. Aligned domains (bunches of bunches) of atoms. This is a quantum property - aligned to macro size.
Domains of material can point in different directions.
Piece of iron may not have a magnetic field at all, because all domains are pointing to different directions.
However if you apply a strong magnetic field from outside the material, you can make one solid unified piece of magnet.
Magnetism is a quantum property magnified to the size of the object.
These criteria are difficult to fulfill. There are few materials that can do that: Fe, Co, Ni, Gd.
Wikipedia:
The magnetization of a magnetized material is the local value of its magnetic moment per unit volume, usually denoted M, with units A/m. A good bar magnet may have a magnetic moment of magnitude 0.1 A·m2 and a volume of 1 cm3, or 1×10−6 m3, and therefore an average magnetization magnitude is 100,000 A/m. Iron can have a magnetization of around a million amperes per meter.
Thanks for the link. But this rule does not always work. In our university laboratory, we used a press to draw stainless steel. After this process, part of the material was magnetized, and part was not. I can not understand how the material properties could change so much.
It depends on the steel grade. Google the article Behavior of steel as a living organism. There this phenomenon was described. My university supervisor was one of the co-authors of the article. Using plagiarism checker for students https://fixgerald.com/plagiarism-checker-for-students (https://fixgerald.com/plagiarism-checker-for-students) I took some of the material for my term paper. So it might be useful for someone else. Interesting analytics and research.