Post by: BilboGrabbins on 21/08/2021 15:14:45
https://www.atticusrarebooks.com/pages/books/719/a-d-sakharov-andrei/vacuum-quantum-fluctuations-in-curved-space-and-the-theory-of-gravitation-in-soviet-physics
https://dx.doi.org/10.1088/1742-6596/1051/1/012017
As abstract his equation may appear, I'll break it down so it can be understood. It won't take long as the premise is easy to grapple. In his paper, he was attempting to explain how early physics didn't believe in the existence of fluctuations, which is described by a divergent integral series where it is taken over the momentum of the ground state of the field and was presumed zero. In his approach, he showed that this not the case (today, we take the existence of these ground state particles now as a matter of experimental fact) but still remains a very hot topic in physics, because it lies now at the very nature of quantum mechanics, where these fluctuations really do come into and out of existence, governed by the creation and annihilation operators: It's a phenom so engrained in physics that Bogoluibov transformations take place in a wide range of physical systems, even black holes that preserve the idea of Unruh-Hawking radiation.
Sakharov's natural insight allowed him to show that higher powers of the metric curvature could sometimes allow virual particles to become real, the contribution of background curvature to the fields.
Sakharov explained that you could expand a Lagrange equation in a geometric series that satisfies
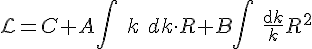
It was so fruitful that he not only obtained a gravitational action
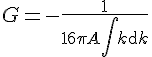
Where
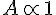but that the geometric series which produced 
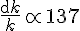the infamous fine structure. It was further discovered that by integration of the wave length yielded the value of 
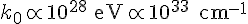, corresponded to the inverse of a Planck length, an indication that the wavelength of the particle was that corresponding to its smallest smearing in space.In Sakharov's equation, he didn't specify all to clearly what the constants of
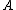and 
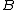where, but its full translation has been written out, the first authors I read who made this equation clear in the context of quantum mechanics came from Arun and Sivaram, they explain the nodes of the field will satisfy Sakharov's Lagrangian in the following way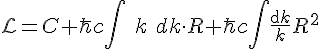
A quick inspection from dimensional analysis upholds this. If
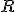is the curvature from Einstein's theory, then it has units of inverse length squared, so inspection from the first part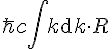
we see is like saying the energy is
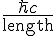
With one extra wave length node
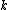and the curvature $R$ is equivalent to a density, so it has units of energy density, exactly what a Lagrangian density should have. Now here is where I invite the "new" physics from some application of calculus.Since we are blessed with the prospect of knowing that the nodes of the field are described by the relatively simple formula using
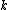as the wave lengths, the inverse can be characterized as the length of the wave, which in physics is given by the speed of the particle by a frequency term. As physicists, we often call it 
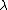and has units of length. We now say that the curvature is a function associated to these waves, so we write a general formula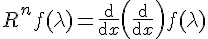
and its differentiation will yield
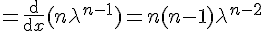
Physicists are often more than not pure mathematicians, we can be quite different animals, but the result is standard enough that to a mathematician, it should be clear that
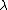becomes our length that has been differentiated like it was in respect to 
. Now we can also define it as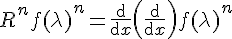
So long as we recognize that
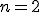and we see now that Sakharov's equation satisfies the differentiation written as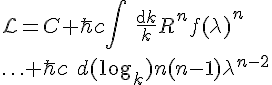
Where we have rewritten
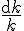as the differential logarithm (and in calculus known as elasticity) of the wave number, and we have replaced 
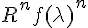with its differential equivalent form of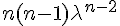 
Post by: Colin2B on 21/08/2021 23:17:21