Post by: BilboGrabbins on 30/08/2021 15:45:55
https://www.thenakedscientists.com/forum/index.php?topic=82903.0
While the crux of this theory isn't entirely essential to the work that will follow, I just wanted to highlight we still don't know the full picture, let's get a taster of the Bohr planetary model and why it still gains traction. It never fully diminished even in ligglht of Schrodingers wave mechanics and even back then, Schrodinger eventually became resentful of some physicists trying to do away with particle dynamics soley for a wave interpretation. He even invented his cat in a box thought experiment to highlight the ridiculousness of a purely random statistical model of physics which contrary to them had been taking significant traction.
A Fruitful Theory
A Brief History Of The Bohr Atom
Mamy think Bohr's model correctly predicted the hydrogen atom energy when in reality 8t did so much more.
1. Bohr kept the Rutherford picture of electrons persuing orbits and predicted that it recerved an inverse square law in a Hill diagram.
2. While in collaboration with DeBroglie, he kept the particle model but used Bohr's equations that linked matter to energy and found discrete and simple laws. For instance, the lowest shelf predicted
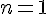as the smallest allowed orbit and soon after Pauli showed with them that the allowed orbits had to satisfy an exclusion principle, which is the opposite to photon behaviour which tended discrete packages to fall into the same quantum states. This way, several electrons could never occupy a shelf, but two could with opposite spins and gave rise to the periodic table.**While Bohr argued certain orbits did not radiate because they didn't follow the usual laws od quantum mechanics, I'll leave as possibly the only ad hoc assumption he made since free fall of orbits answers it sufficiently with accepted laws. Even planets orbiting the sun are in free fall.
3. Bohr predicted the size of the hydrogen atom. There's been a lot of dialogue so far and I just want to get throughthis as quick as possible to the work I wish to present. If yoy would lije mathematical demonstration of this, please just ask in a post. By working out the size of the hydrogen atom, he was effectively calculating the diameter of an electron in the outermost shelf.
4. Arguably his greatest achievement was his prediction of bright spectral lines which at that time was crying for an explanation and had dumbfounded even the brightest minds up till that point.
5. He correctly predicted the fine grating spectrum constant. The value he obtained was experimentally obtained eventually as 3286 trillion compared to his agreement of 3290. For many, the agreement was so precise, it validated his theory to a lot of resistant, suspicious minds.
6. He was capable of measuring the transition of those orbits. In fact, my work below encompasses the same idea, ge write the transition as:
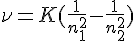
In fact, this equation is called the Rydberg formula and was adopted into his work. Bohr went as far to say, it was a universal equation which was fundamental to a large number of physics which used discrete processes. This is one of the reasons why it will feature a lot later in my own work.
7. Bohr predicted the exact nature of the Helium atom. He presumed that we could envision a Helium atom that had lost two of its electrons and the remaining electeon would emit light when switching orbits. With the one remaining electron, it behaved like an ionized Helium atom which is like a Hydrogen atom with a doubling controlling charge +2e on the nucleus. With Z = 2 (the nuclear charge) the predicted frequences were just 4 times than the Hydrogen frequencies. These lines had been discovered previously, but before Bohr's model, it had been mistakenly takebln for a Hydrogen atom in some strange and special state.
8. Bohr using his model not only predicted this ionized half-stripped Helium but even predicted a minor correction from the nuclear mass from which he was capable of measuring the electron to proton mass ratio as 1/1830.
9. Then his theory predicted the switches of innermost electrons that would produce x-ray frequencies far greater than the visible light spectrum because the constant K had for it Z^2.
So while we might be taught often to drop this planetary model, it is still the only successful theory that has managed to predict all features of quantum physics above. This is why Bohr's model won't be superceded. There has to be some aspect of the planetary model to be true because its highly unlikely he was able to derive these results by pure chance alone. If it had been by chance, then it's been the most successful "accident" ever predicted for atomic physics.
Now To My Theory
When reading Lloyd Motz'wirk on the Uniton (a proposed primirdial particle not too dissimilar to a primordial micro black hole) he stated that Weyl invariance suggested a quantization of mass as
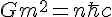
And said it was equivalent to the charge squared analogue. For years I just accepted that, then when doing some preliminary equations to find a charge relationship to the orbitals inside an atom to obey Keplers law of motion which soon brought the analogue into a new light. I first came to hypothesize from derivation
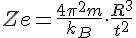
From there I made a suggestion that we set
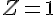for the special case of a hydrogen atom and then 
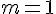for a sufficiently small electron mass and came to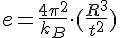
But then I decided to meddle around, seeked a unification from the inspection of the similarities between electrostatic laws and those with gravity, and found unlike what Motz had claimed,
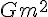waa not the analogue of charge squared alone, instead I found it must satisfy a slight alteration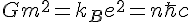
In such a case now, we can loosely say that mass is the analogue of the charge and Newtons constant is the analogue of Boltzmann's constant. In cgs units Newtons constant is
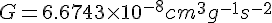
In cgs units, Boltzmanns constant is
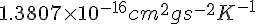
When I recalibrated my equations, for an electric charge round the nucleus, I eventually derived
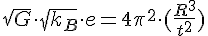
And I ended up with a mixture of the two constants, one which measures how gravitational objects interacted and the other how thermodynamics applies to the motion of systems. I went off, took the two and made a new constant out of it, let's call it K and this time the corrected formula for a charge round a nucleus preserving Keplers law and became
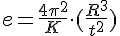
A while ago, I submitted a paper in a competition to the gravitational research foundation but I dropped this topic back in 2018-2019 for an attempt on a pseudo quantum picture of gravity which modelled curvature in a Hilbert space without gravitons. The original paper I had outlined in mind was a full translation of the Rydberg constant with DeVroglie wave mechanics and a fully coherent theory of how phase transitions occurred for any system preserving the loss or gain of discrete packets of quanta. I managed to derive that constant with units of inverse length:
*quick note: I was impressed how my original calculations came to that called a Holeum model and gave me insight that at the very least, I derived my own formula from the correct ingredients even expanding it into a relativistic equation, which I had never seen in a transition formula before.
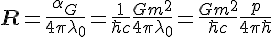
Where the last term managed to pick up DeBroglies famous relationship to matter and waves. I then asked, "What if the Rydberg constant was related to the change in the wavelength using the universal equation" as Bohr had called it?
So I did and I got:
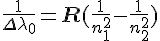
Then to get the energy transition was easy and we pick up
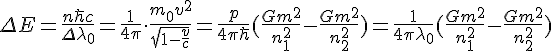
While my theory thus far had nothing to with the Holeum model, my results were very close and told me that instead if a two black hole particle model orbiting each other, this transition formula could describe a single black hole undergoing discrete transitions. Whether the black hole was increasing mass or loosing mass via the evaporation phase, both physics appeared very interesting in light of my formula. What do the limits in the equation mean for discrete transitions of a black hole?
We can change the formula slightly and write it for a change im the mass and write the wavelength as a thermal wavelength,
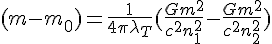
Then as
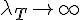
Then
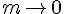
So for a black hole, as the thermal wavelength increases, the black holes mass decreases as we would expect. It means that as it looses mass due to Hawking evaporation, the black hole conserves the idea of it getting hotter. We have no exceptions in physics, mass was shown by DeBroglie to always satisfy
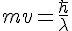
And this even applies to tennis balls, not just particles. It's just that the bigger the mass, the smaller associated wavelength there is. It's not impossible to apply the uncertainty principle to the model either. I did so and it falls out like
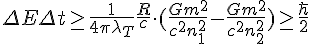
Where
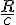is the invariant time operator. This is just a nice inbetween post as I have been given permission to writeup a thread on bivector gravity. It's one of the most interesting theories I ever looked into and I think I was one of the first to explore it in depth like I had. So expect at some point I'll br writing up about this theory.
Post by: BilboGrabbins on 30/08/2021 16:00:23
Post by: Bored chemist on 30/08/2021 22:50:06
Even planets orbiting the sun are in free fall.And the evidence suggests that they emit gravity waves, just as an orbiting electron should emit EM radiation.
He correctly predicted the fine grating spectrum constant.The what?
. Bohr predicted the exact nature of the Helium atom. He presumed that we could envision a Helium atom that had lost two of its electrons and the remaining electeon would emit light when switching orbits.How many electrons do you think a helium atom has?
Maybe I should be clear
Maybe...
Post by: BilboGrabbins on 01/10/2021 01:53:53
Even planets orbiting the sun are in free fall.And the evidence suggests that they emit gravity waves, just as an orbiting electron should emit EM radiation.
[/qoute]
I don't feel any need to answer the other quotes, you're a bit pretentious at times. However I'll note that gravitational radiation is a bit different to electromagnetic radiation if we are clear on one aspect, gravity doesn't appear to be quantized as it is a pseudoforce. So the radiation from gravity is a metric thing, rather than a phenomemon from mediator particles. Perhaps, in the context of gravity it's wiser to say all particles curve space, all fields contribute to gravity. Therefore gravitational waves is associated to all dynamics, not just those associated to massive bodies orbiting a common center.
Post by: BilboGrabbins on 01/10/2021 02:30:16
If the transition formula is to be believed, and if applied to the discreteness of black hole energy levels, then why is there an associated large wavelength for a mass approaching zero, but still retaining an idea that smaller black holes give off more thermodynamic heat?
I'm not saying I'm wrong, but for it to get hotter, it would need to, in this picture give off much more longer wavelength particles, and as it grew, much less particles but with smaller wavelengths. Something has to give here, and the reason why is because in conventional physics, the hotter an object, the shorter the wavelength of its peak emission. So we might think, well in that case small black holes must give off waves of shorter wavelengths, but you wouldn't think that from the relationships I looked at.
Maybe its still right, perhaps thd accounting of a hotter black holes just comes from the rate of emission and may not be held to the issue of short vs. long wavelengths in general.
Post by: BilboGrabbins on 01/10/2021 02:42:03
Post by: BilboGrabbins on 01/10/2021 15:18:52
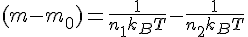
And as you see, the transition certainly does state here that as mass goes down, temperature increases. So I'm no longer doubting the validity, but it imposes that perhaps the interpretation of the wavelength is wrong. Put it this way, if it is right, it throws a different type of model into theoretical physics, because we currently think large black holes should only be able to eject Hawking radiation with ease because they have large wavelengths. A cite for this statement can be found here
https://www.google.com/amp/s/www.livescience.com/amp/33602-particles-escape-black-holes.html
So either I'm right or wrong, you can chose. I don't really care to. I would quickly like to go back though to this equation
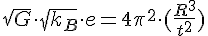
I said we ended up with a strange mix of gravitational and thermodynamic constants, which the latter plays a role in electromagnetic theory... but is it really strange? Well, working out the dimensions of these twi constants, we can derive from dimensional analysis, which is a powerful tool, that
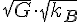
And I get
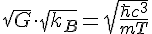
We'll find an argument that 8 pi should be a coefficient in the denominator as
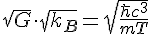
Just a bit of quick algebra, the square root of c^3 is just c sqrt(c) or c^3/2. I don't derive 8 pi but we'll see in a moment why it is probably there. Now, armed with this, we can rearrange to find for the temperature and you get
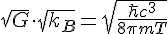
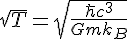
Does it look familiar? It should because its the Hawking temperature, you'll recognize it more accurately as
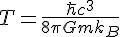
So we have what we identified
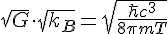
And my result of
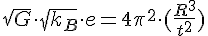
If we square everything and just plug it all together, we'd have without those nasty looking radicals,
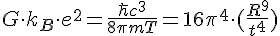
If the numerics are fine, we can suggest a few different equations from this but the one I appealed to first was
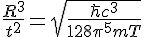
It gives me some new line of enquiries to look into. I can't be sure at the monent if 128pi^5 should arise in there, as I did not derive that part, this was just from hopeful guesswork. It might be that you can in fact derive the temperature
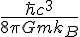
From
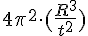
And perhaps you might get 8\pi from 4\pi^2 as they are not so indifferent, I'd need to look into that with depth. It might, you need to be careful and not to careless on guesswork
Post by: Bored chemist on 01/10/2021 18:23:06
I don't feel any need to answer the other quotesThen you should think carefully about what a discussion forum is for, and whether you are in the right place.
.
you're a bit pretentious at times.I don't think you know what the word means.
gravity doesn't appear to be quantizedUnless, of course, it is.
https://en.wikipedia.org/wiki/Graviton
I'm not saying I'm wrongI am saying that.
Post by: BilboGrabbins on 02/10/2021 00:02:26
Post by: Bored chemist on 02/10/2021 12:08:43
The community are secretely awareOh, so you are launching a conspiracy theory.
That's interesting.
Please do it somewhere else.
Post by: BilboGrabbins on 03/10/2021 07:00:44
The community are secretely awareOh, so you are launching a conspiracy theory.
That's interesting.
Please do it somewhere else.
You talk so much rubbish sometimes.