Post by: BilboGrabbins on 30/08/2021 19:57:02
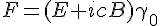
Where E and B are the respective electric and magnetic fields. I was massively curious how this would transcend to gravity. I noticed that in bivector gravity, a part of the algebra encodes a spin space and that jumped out to me as important for a theory satisfying a full Poincare group of space symmetries. To start oc I modified the d'Alembertain operator accordingly and it took the form of;
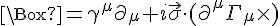
This is just a convienient way to write the operator in terms of curved spacetime where we recognise
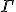as the Christoffel symbol. What we notice under bivector gravity is the spin Pauli vector 
has attached to it an imaginary number. This is the only exception we can allow a complex number into a theory of gravity since gravity is manifestly non-complex. Using these ideas we make a simple theory of gravity with two derivatives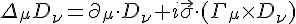
D can be any space ortime derivative. Anyone accostomed to GR will know we just describe curvature and gravity by these "connections." Here ot is vital to understand the importance of the lasr term and I identify it as gravitational torsion
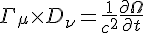
A similar idea of torsion arose in previous work, where I attempted to describe its effects on the particle scale
https://www.thenakedscientists.com/forum/index.php?topic=82903.0
In both cases, torsion there and here are ascribed with dimensions of inverse time. So the LHS has dimensions of inverse length squared, just as it is on the RHS. This cross product if the field and the derivative making torsion is not new, (I think Heaviside might have derived it in this way, but not sure now) but I noticed it falling out of our theory in a natural way, on the spin space of Pauli vectors.
As I said, anyone aquainted with general relativity, we deal with the products of derivatives, frequently. A good example is when deriving the curvature tensor of GR and just looks lije:
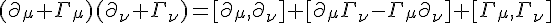
In ordinary approach from GR, the torsion is said to arise from this part
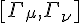
Whereas in our theory it arises in
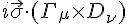
Before I move onto the kinetic energy of spin with the same ideas surrounding the bivector set up, let's investigate a fuller description of the two derivative idea and attach the conventional gamma matrices onto it. A quick reminder of those matrices can be found here
https://en.m.wikipedia.org/wiki/Gamma_matrices
We will quickly note that any timelike gamma matrix is always denoted with a naught
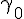and the spacelike ones are denoted with indices (1,2,3). Now we can say the bivector gravity will satisfy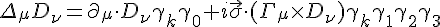
And we can calculate the derivatives in a similar way we would derive the curvature tensor, hence why it was important to feature it earlier. Not just to show the differences of how torsion arises in this theory compared to GR, but how the derivatives are now formally calculated with the gamma matrices.
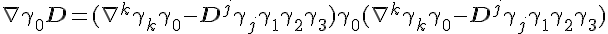
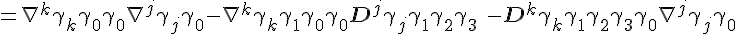
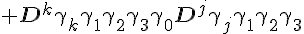
So aside from using all the fancy gamma matrices, we can still retrieve a theory similar to that obtained by Einstein where the last part
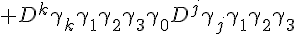
Has a structure similar to the torsion in GR. Some algebraic properties you may need to come to know is
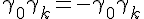and another useful one is 
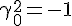. It's also true that 
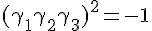. A fun fact is that space and time may not even commute. That is, any product of two classical space derivatives may not be equal to zero. This is called the spacetime uncertainty principle, and there may be evidence of this according to some from scattering experiments.Ok, so that big formula above with all those gamma matrices atrached to it, we realized looks a lot like a curvature tensor that you might calculate from GR. If the curvature tensor is just a product of two derivatives, can we not just say
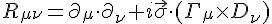
It might be, I even wrote this down in my notes. You might even theorise a stress energy tensor in a similar fashion:
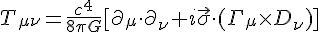
Truth is I don't know if it's right or wrong, a lot of it was guesswork. What I did notice the algebra can fit a number of different physics. For instance, the hydrodynamic time derivative is
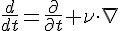
You can see how this equation could reinterpretated as
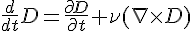
Related to fluid and kinetic motion, I looked at the total angular momentum
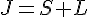
I took a really simple approach. Just meddling and merging some ideas together. For instance, similar to the correction term in GR on flat space is just an additive feature in the covariant derivative
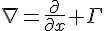
Then I looked at some old theories of how the angular momentum L was described interacting with a torsion field. I can't remember who first wrote it, I know Heaviside might gave first written it, but the "moment of forces" equation was
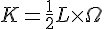
Where
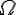was the torsion. By plugging in the total angular momentum and rewriting it like a bivector theory I got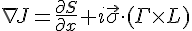
And the last term looks like a torsion, albeit, it's directly written as the connection.
While writing this, I looked into some of the history of Heavisides equations ans found this interesting;
https://en.m.wikiversity.org/wiki/Heaviside_vector
Heaviside in its most simplesr form, said torsion was related to gravity like
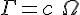
Which almost fits my dimensions from
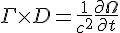
I don't know just by looking at it how he defines his dimensions here, he might be ascribing field as acceleration, in which case the torsion has dimensions of time exactly as opposed to my approach of inverse time. Both ways are just as good. You can define a Christoffel symbol with dimensions of acceleration or as a space or time derivative. Some are even dimensionless.
He was able to define his own vector, ignoring some constants, his vector identified a torsion relationship with the Christoffel symbol as
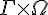
And I defined it as
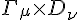
Which is very similar. If the derivative D was taken as the torsion directly, then yea, our theories would meet eye-to-eye. Just a recallobration of units and the ideas are the same at the crux of it. I look back on questions I asked a long time ago and it seems I was puzzled by it even back then
https://physics.stackexchange.com/questions/467765/heaviside-vector-units/472807#472807
While searching, I even found myself asking physics exchange on whether there was a functional theory of bivector gravity and we can see some of my preliminary thoughts here
https://physics.stackexchange.com/questions/463682/is-there-a-geometric-algebra-for-gravity
Higher Dimensions
I refer you to wiki's page ob this bivector theory as it speaks about higher dimensions
https://en.m.wikipedia.org/wiki/Bivector
These mathematicians are way over my head. When I was formulating the theory, before this wiki article clearly had tweaks over the years, I made a statement that there was a stringent result on the dimensions, and this is because cross products cannot operate in any other dimensions other than three or seven. Here I go into lengthly detail about a bivector gravity and why it should only work in three or seven dimensions. I ended up answering my own post:
https://physics.stackexchange.com/questions/448809/geometrized-algebra-and-einsteins-equations
I even remark how GR is a theory of curved space and time and how a bivector theory of say three dimensions while not impossible, would be a hard sweet to swallow. I know there are certain physicists out there who meddle with the no-time hypothesis.
But! It just shows you I couldn't have known much back tjen, because since then the wiki article explains how to do deal woth bivectors above four and even more dimensions. It seems I was fixated on the issue of cross products only working in three or seven dimensions and a bit foolishly I guess, just assumed it would extend similarly to a bivector theory of gravity. I wasn't and still not, a big fan of extra dimensions and a limiting case to three appealed to me wthoit fully understanding its complexities. Soyeah, in short I can be wrong. Probably more times than I'd wish to believe!
Post by: BilboGrabbins on 30/08/2021 20:00:36
Post by: BilboGrabbins on 30/08/2021 20:04:33
Post by: BilboGrabbins on 30/08/2021 20:15:51
Post by: BilboGrabbins on 30/08/2021 20:19:37
Post by: Colin2B on 30/08/2021 23:13:15
There seems to be a site bug on the equationThe Simple Machines engine the site runs on doesn’t seem to carry the full Latex set. I’ve run into problems occasionally which is why I don’t usually engage on such posts, can be hard work replying. Often you can work around the issue with other options.
Post by: BilboGrabbins on 31/08/2021 01:54:49
There seems to be a site bug on the equationThe Simple Machines engine the site runs on doesn’t seem to carry the full Latex set. I’ve run into problems occasionally which is why I don’t usually engage on such posts, can be hard work replying. Often you can work around the issue with other options.
I ran across it once before, I seem to have gotten lucky this time and found a way round it.
Post by: Kartazion on 31/08/2021 05:41:41
These two publications should interest you:
Bivectors in Newman-Penrose formalism in General Relativity -- from electromagnetism to Weyl curvature tensor https://arxiv.org/abs/2108.07167
Bivector Formalism in General Relativity https://www.researchgate.net/publication/350520902_Bivector_Formalism_in_General_Relativity