Post by: Eternal Student on 01/09/2021 23:21:42
What proof or good reason exists for suggesting that all physical systems that we might want to study can be modeled with a Lagrangian and a least action principle?
I honestly don't know. Why is Nature lazy and always trying to minimise an action?
Biologists and Chemists welcome - please check this and comment if it's wrong:
Chemists and Biologists don't seem to assume that every system they want to study and model can be represented with a Lagrangian. I'm fairly sure that when a vaccine for Covid was developed no one started by proposing a new Lagrangian for the system.
Best Wishes.
Post by: evan_au on 02/09/2021 10:10:21
Quote from: OP
LagrangianLagrange was a very productive mathematician. Which Lagrangian do you mean?
Quote from: Wikipedia
Lagrangian may refer to:
Mathematics
- Lagrangian function, used to solve constrained minimization problems in optimization theory; see Lagrange multiplier
- Lagrangian relaxation, the method of approximating a difficult constrained problem with an easier problem having an enlarged feasible set
- Lagrangian dual problem, the problem of maximizing the value of the Lagrangian function, in terms of the Lagrange-multiplier variable; See Dual problem
- Lagrangian, a functional whose extrema are to be determined in the calculus of variations
- Lagrangian submanifold, a class of submanifolds in symplectic geometry
- Lagrangian system, a pair consisting of a smooth fiber bundle and a Lagrangian density
Physics
- Lagrangian mechanics, a reformulation of classical mechanics
- Lagrangian (field theory), a formalism in classical field theory
- Lagrangian point, a position in an orbital configuration of two large bodies
- Lagrangian coordinates, a way of describing the motions of particles of a solid or fluid in continuum mechanics
- Lagrangian coherent structure, distinguished surfaces of trajectories in a dynamical system
Maybe we can reach it this way? https://en.wikipedia.org/wiki/Stationary-action_principle
Post by: hamdani yusuf on 02/09/2021 11:23:30
Which Lagrangian do you mean?When I first read th OP,
Chemists and Biologists don't seem to assume that every system they want to study and model can be represented with a Lagrangian.I assumed that he referred to Lagrangian mechanics.
https://en.wikipedia.org/wiki/Lagrangian_mechanics
Quote
Lagrangian mechanics defines a mechanical system to be a pair (M,L) of a configuration space M and a smooth function L=L(q,v,t) called Lagrangian. By convention, L=T-V, where T and V are the kinetic and potential energy of the system, respectively. Here q ∈ M, and v is the velocity vector at q (v is tangential to M).CMIIW.
Describing a system using its kinetic and potential energy is also the idea behind Schrodinger equation, which is used by chemists, as shown in this 60 seconds video.
Post by: TommyJ on 02/09/2021 14:41:36
The article explains all details, history, disputes and the ‘See also’ part is very useful.
https://en.wikipedia.org/wiki/Stationary-action_principle
As for vaccines, the principle of least action might be explained like this.
Any approach from state or point A to B takes a path that minimizes ‘something’: curves, spirals, anything.
‘Something’ is the action (A), which is described with:
- how fast is it going (K)
- position, where it is now (P)
A = K - P of the object in the entire path.
A= ∫ (K - T) dt
Post by: Eternal Student on 02/09/2021 18:38:57
Which Lagrangian do you mean?I probably should have said more in the OP but the answer was always in the title:
"Lagrangian Mechanics - Why is nature Lazy?"
For a simple mechanical system, the Lagrangian, L = K - V
where K = kinetic energy of the system; V = potential energy of the system. ....etc..
Hamdani correctly provided this reference:
I assumed that he referred to Lagrangian mechanics.
https://en.wikipedia.org/wiki/Lagrangian_mechanics
Anyway, you (all) have the right idea. That is the Lagrangian and the least action principle that I am asking about.
However, Lagrangian mechanics is not limited to considering just simple mechanical systems. The Einstein Field Equations can be derived from a least action principle and a suitable Lagrangian (See Hilbert-Einstein Action in Wiki if you're interested, https://en.wikipedia.org/wiki/Einstein%E2%80%93Hilbert_action). Most field theories involve a suitable Lagrangian [ https://en.wikipedia.org/wiki/Lagrangian_(field_theory) ]. In general, it seems like most physical systems can be described with a suitable Lagrangian and then a least action principle will describe the evolution of the system from an initial state to a later state.
Hamdani mentioned quantum mechanics which is perfectly sensible since it has a Hamiltonian in it - but it is a little bit of side-step from the main topic. Hamiltonian mechanics and Lagrangian mechanics are very similar and we can often derive one from the other. However, in general Lagrangian mechanics is considered as the parent technique and identifying a Lagrangian to describe a system is preferred rather than identifying a Hamiltonian.
If you want more information, see https://en.wikipedia.org/wiki/Hamiltonian_mechanics and note that to define quantities like the generalised momenta pi we often assume the Lagrangian, L is already known, since pi =
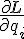However, none of this really needs to concern us too much - I think it's fair to say that Lagrangian mechanics is the parent technique but the differences are not worth worrying about. Both techniques assume there is an action, S(x), and a system evolves from one state to anther so that the action functional is stationary.Also, yes, I acknowledge that Chemists use Lagrangian mechanics when they are actually doing Physics. However, I think that most Chemistry is done with orbital and bonding theory and this is an "effective theory" that was only loosely based on solutions from Quantum Mechanics. For example, when developing the vaccine for Covid someone probably did model a new molecule with the ideas of p orbitals and π and σ bonds. However, it seems unlikely that they solved the Schrodinger equation to find an exact solution for that particular molecule.
Anyway, back to the original question:
Can all Physical Systems be modeled with a Lagrangian?
Why would a system evolve in such a way as to minimise (or at least find a stationary value of) the action?
Best Wishes.
Post by: Eternal Student on 02/09/2021 18:49:14
Sorry I didn't directly take a quote or acknowledge your reply. Anyway it's perfectly good apart from one minor typing error:
A = K - P of the object in the entire path.In the top line that is L, the Lagrangian not A. But obviously you knew what you were talking about.
A= ∫ (K - T) dt
Anyway let's take your answer directly:
Any approach from state or point A to B takes a path that minimizes ‘something’: curves, spirals, anything.Why is Nature lazy? Why does it always want to minimise something?
‘Something’ is the action (A)
What actually makes you so sure there is always a thing, the action, that we can define and Nature would want to minimise that?
Post by: Bored chemist on 02/09/2021 18:57:39
Chemists and Biologists don't seem to assume that every system they want to study and model can be represented with a Lagrangian. I'm fairly sure that when a vaccine for Covid was developed no one started by proposing a new Lagrangian for the system.As far as I can tell, that statement is correct for any of the given uses of the word.
My understanding is that Lagrangians are only useful for simple "toy" systems like physicists use. (Statisticians do a similar thing with Normal Distributions)
I seem to recall using Lagrangian multipliers for something once. Specifically, I used them to pass an exam in 1985, and then I forgot about them.
Post by: Bored chemist on 02/09/2021 19:00:09
For example, when developing the vaccine for Covid someone probably did model a new molecule with the ideas of p orbitals and π and σ bonds.I wouldn't bet on that.
With big molecules you might as well model them as balls on springs.
Post by: TommyJ on 02/09/2021 19:52:01
Why is Nature lazy? Why does it always want to minimise something?Thank you, for understanding and clarifying the question.
What actually makes you so sure there is always a thing, the action, that we can define and Nature would want to minimise that?
My first explanation was rather 'project management' approach: where we are, were we need to get (result), and what time we have to get the result?
Nice that many things in other areas come to differential equations.
The question on the level of biology/chemistry/physics is deeper. Probably they went with experience, knowledge and trials, and the nature of viruses just follows the nature.
1. Do the biologists and chemists use similar equations? (I was always trying to escape with math from that) - needs answer.
2. Why Nature evolution goes like this 'lazy' way and if it does it all the time? - needs answer (probably or approximate hypothesis comes to some of 'energy conservation' and entropy answers?).
Post by: Bored chemist on 02/09/2021 21:38:36
Do the biologists and chemists use similar equations?Please pardon my ignorance, but similar to what?
Post by: alancalverd on 02/09/2021 23:11:48
We have discussed elsewhere that energy is simply "that which is conserved" so in a fully described (i.e. closed) system, ΔK = -ΔV by definition, so the most probable path is B→C with ΔS > 0.
Post by: evan_au on 02/09/2021 23:13:00
Quote from: Tommy J
Do the biologists ... use similar equations?The Least Action Principle refers to "the action is stationary (no change) to first order".
- This implies that there is some differentiable function describing all the alternative ways the system could evolve
- And the path taken is the path which has a stationary point (minimum, maximum or saddleback in some multiple-dimensional space).
However, at its heart, biology is based on genetics, which is digital rather than analog.
- Differentiating digital functions rarely produces stationary points (unless the digital function is a constant)
- So genetic changes in the offspring can produce no visible change, or a total change (death), or somewhere in between.
- And it can be the same change (eg changing a DNA letter from A to C) that can produce any of these wide variety of outcomes
- One change (A to C) might change the color of your hair, while the same change in a different part of your DNA may provoke early-onset diabetes.
- Both changes have the same action. But because it is digital rather than analog, the effort to make the change is non-zero, so the code is (in some sense) preserved; the system does not slide smoothly from one state to another state, as implied by the Least Action principle, guided by a Lagrangian.
Post by: hamdani yusuf on 02/09/2021 23:35:35
Anyway, back to the original question:AFAIK, any Physical Systems which can be modeled with Newtonian mechanics can also be modeled with Lagrangian mechanics.
Can all Physical Systems be modeled with a Lagrangian?
Why would a system evolve in such a way as to minimise (or at least find a stationary value of) the action?
Why would a system evolve in such a way as to maximize entropy?
Post by: Eternal Student on 03/09/2021 00:40:03
We have discussed elsewhere that energy is simply "that which is conserved" so in a fully described (i.e. closed) system, ΔK = -ΔV by definition, so the most probable path is B→C with ΔS > 0.This sounds perfectly sensible to me. It sounds like statistical mechanics with ΔS as the usual symbol for the change in entropy. It's obviously a (perfectly reasonable) way of predicting how a system may evolve. It doesn't seem to be easily formulated as a least action principle. So were you proposing that the evolution of some systems cannot be described by a Lagrangian and a least action principle?
- - - - - - - - - -
However, at its heart, biology is based on genetics, which is digital rather than analog............(and so derivatives and a least action principle don't necessarily apply)
Yes, thanks for that evan_au. This also seems sensible to me.
I just needed to check that Biologists and chemists aren't unhappy with the idea that they do not assume every system of interest to them can be modeled with a Lagrangian and a least action principle.
Anyway, it's just what we need as fuel for the main thrust of the question: Why do Physicists assume that every system of interest to them can be modeled this way?
Best Wishes.
Post by: Eternal Student on 03/09/2021 01:04:57
AFAIK, any Physical Systems which can be modeled with Newtonian mechanics can also be modeled with Lagrangian mechanics.Yes.
....and for Newtonian systems, it's not too difficult to explain why a least action principle would apply when the Lagrangian is constructed in the usual way as K - V (Kinetic - Potential).
I should probably make it clear that some scientific dictionaries will state that "Lagrangain mechanics" means only the Lagrangian formulation of what could otherwise be a Newtonian system. However, I am using the term "Lagrangian Mechanics" in a much broader sense. Any system that can be represented with a suitable Lagrangian and a least action principle, i.e. so that it "looks like" Lagrangian mechanics but the Lagrangian is more elaborate or abstract and the "generalised co-ordinates" do not just refer to the properties of particles.
See, for example, the Lagrangian formulation of classical field theory. https://en.wikipedia.org/wiki/Lagrangian_(field_theory)
Why would a system evolve in such a way as to maximize entropy?I suspect this question was aimed at Alancalverd's earlier reply.
Best Wishes.
Post by: Eternal Student on 03/09/2021 01:47:39
Perhaps I should explain why I'm interested:
There has been a "fashion" or a "passion" for expressing new Physics with a Lagrangian and a least action principle.
Why is this?
Examples:
1. General Relativity. Einstein and Hilbert developed a suitable "Action" so that the Einstein Field Equations could be derived from a least action principle. They did this some time AFTER General Relativity and the E.F.E. had been published. For some reason, it was felt important to show that you could use a Lagrangian formulation if you wanted to. Apparently, it gave more credence to General Relativity.
2. Noether's theorem. As far as I can see, this says nothing about general physical systems and symmetries. The entire paper published in 1918 only manipulates Lagrangians and describes conserved quantities that will exist and symmetries that will be present in the Lagrangian. If you can't express a system with a Lagrangian then there is no reason to believe that Noether's theorem has any bearing on it at all. (Don't get me wrong - this is some reason to hope that all physical systems can be represented with a Lagrangian. There seems to be enough confidence that this is true that Noether's theorem is just assumed to apply to all physical systems).
3. Lagrangian mechanics started as an alternative formulation for Newtonian systems. It was very successful. The ideas seem to have then spread far and wide. Almost everything is now represented with a Lagrangian. However, I have never seen any proof that every physical system can be represented with a Lagrangian or exactly why Nature should always want to minimise something (this "something" being what we can call the action).
Don't worry yourselves too much about it. I honestly don't know why Nature is lazy and why there should always be a quantity we can identify as a Lagrangian. Chemists and Biologist's don't seem to think that there's a Lagrangian for every problem and every system they want to examine.
Best Wishes.
Late editing: Changed "some years after" to "some time after". I can't find a reference for exactly how much time had passed, just that it was after.
Post by: Bored chemist on 03/09/2021 08:48:19
Chemists and Biologist's don't seem to think that there's a Lagrangian for every problem and every system they want to examine.There may be one (I don't know), but it doesn't seem to be the most practical way to a solution.
In principle, there's an electron wave function of every nut and bolt in a car (and for the car as a whole).
But it would be absurd for a mechanic to calculate them.
Post by: TommyJ on 03/09/2021 09:34:36
'Lagrangian mechanics' is a foundation to many fields. I know better of its principles to be used in economics.Chemists and Biologist's don't seem to think that there's a Lagrangian for every problem and every system they want to examine.There may be one (I don't know), but it doesn't seem to be the most practical way to a solution.
In principle, there's an electron wave function of every nut and bolt in a car (and for the car as a whole).
But it would be absurd for a mechanic to calculate them.
I have got a consultancy from medical experts.
For medical practices there is no ready model (which can be expressed by equations), there is previous experience (that might be put as potential energy analogue) with lots of statistical data, and a vector, which is applied to ‘draw’ the path with experiments. And sometimes this path goes more or less steady, giving a trustable result. But in some cases it may have an unexpected turn, that gives new statistical data and experience to start again.
In the case of RNA vaccine, the result might really look as ‘0’ or ‘1’. But still it is probabilistic model.
RNA gets into a cell, it instructs the cell to make the SARS-CoV-2 spike protein for the immune system to respond to. It depends on a certain state of the immune system of a person.
For me, to put it to a model, this is a Machine Learning principle. Putting result to ‘0’ or ‘1’, where ‘1’ - should be vaccine applicable to a majority of people with certain features (e. g. age, blood type, etc.). Then run tests.
Post by: alancalverd on 03/09/2021 11:00:33
So were you proposing that the evolution of some systems cannot be described by a Lagrangian and a least action principle?Quite the reverse! L = K - V applies, but you asked why nature is lazy and the reason is that by definition the most probable evolution is the one where ΔS > 0 whilst conserving K + V.
However I do note some potential confusion as S (not S) is often used as the integral of L!
I am slightly uneasy with the thought that folk might confuse the model L with the reality, hence the anthropomorphic concept of laziness. If you start with the statistical mechanics and the axiom that the most likely outcome of an evolution is that which is most probable (all the best axioms are tautologies!) and the experimental observation that
K + V is conserved, you can work backwards to your Lagrangian analysis of energy transfer.
I'll happily admit to taking an engineering approach to most subjects, but it must be remembered that thermodynamics owes more to the development of the steam engine than the steam engine owes to the development of thermodynamics! Most physics begins with product failure.
Post by: Bored chemist on 03/09/2021 11:55:59
For me, to put it to a model, this is a Machine Learning principle. Putting result to ‘0’ or ‘1’, where ‘1’ - should be vaccine applicable to a majority of people with certain features (e. g. age, blood type, etc.). Then run tests.We already know that we need to run tests, what tests to run and how to interpret the results.
What does the extra number crunching add?
Post by: TommyJ on 03/09/2021 12:26:40
What does the extra number crunching add?Usually - more precision or additional model. Let's see after several months, what will change. Pandemic is here to stay for a while, and news about statistics, numbers, behaviors become public regularly.
Post by: Bored chemist on 03/09/2021 14:16:45
Good luck.
Post by: Eternal Student on 03/09/2021 17:21:01
I am slightly uneasy with the thought that folk might confuse the model L with the reality, hence the anthropomorphic concept of laziness.I would agree with that. It's just a bit easier to antropomorphise and say the Nature is "lazy" rather then keep saying that for some reason, systems evolve so that the path of evolution is a stationary value of something.
Let's take another example: In Newtoninan mechanics, it is stated that objects naturally follow straight lines (unless something mucks this up and then we believe there was a force acting). This makes sense as far as it needs to.
We can even try to explain why this should be the case: Consider an object with some velocity v . If space is isotropic then it has no reason to turn in any direction, so it just goes along in the directon of the velcoity for a while. In the new place, it finds exactly the same thing and exactly the same rules should apply (since space is homogeneous). It just should keep going and it all seems to follow from the idea that there is nothing special about any direction in space or any place in space.
In General Relativity we have to give up the straight line argument. Objects tend to move along geodesics. What is a geodesic? It's a path that finds a stationary value of the proper time.... there we go again.... why is Nature concerned about maximising or minimising something? Or if we avoid anthropomorphising nature.... why is this an adequate explanation for the motion of a particle? Why should maximising the proper time experienced by the object in moving from an initial event to another event be important?
I don't know. Feynamn talked for a while about qunatum particles taking every path. Maybe that's all there is, particles don't take geodesic paths, Nature has no problem with them taking every path. It's just that a path that maximisies the proper time is the most probable when some superposition of a wave function is applied. I honestly don't know.
Best Wishes.
Post by: evan_au on 03/09/2021 23:13:12
Quote from: OP
Chemists and Biologists don't seem to assume that every system they want to study and model can be represented with a LagrangianWhen a protein molecule is being assembled by a ribososome, it is a linear string, continually being jostled by water molecules, salt ions and general thermal motion.
- Rather than forming random strings, balls and knots, it usually ends up in a very particular shape.
- This is due to the fact that some parts of the protein are more positive or more negative, or more hydrophobic or more hydrophilic, so some shapes will be more stable than others (ie the protein end up with a slightly lower potential energy, and the water molecules end up with a slightly higher kinetic energy: that sounds a bit like a Lagrangian?)
- This process is slightly aided by the protein being formed in several strands, and being spliced together or cut apart by enzymes, or self-assembling due to mutual attraction.
- There are several genetic spellings for each amino acid (61 sequences which specify 20 amino acids), not all of which have equal concentration in the cell. I have seen suggestions that some of these "slower" DNA sequences might allow more time for the protein to settle into the right conformation before adding more protein units.
Biologists have the opposite problem: they have a string of DNA letters, from which they can deduce a list of transcribed mRNAs (or read the mRNAs directly). They can tell what linear string of proteins will be produced by a ribosome, but it's incredibly hard to tell what shape the protein will fold into.
- The traditional method was to extract and purify the protein, crystallize it and obtain X-Ray diffraction images. But some proteins are resistant to crystallization, or break down too easily, or just fold into a different shape when the water is removed (all these problems plagued Rosalind Franklin when studying the structure of DNA).
- Computer modeling has been used to find shape of a protein with the lowest potential energy, but it requires big computers
- More recently, it has been turned into a competitive computer game: FoldIt
- It looks like Google has got into the act with AlphaFold, which is trying to emulate humans playing FoldIt, but taking into account the success rating from tests in the lab to produce a better prediction.
See: https://fold.it/portal/info/about
https://deepmind.com/blog/article/AlphaFold-Using-AI-for-scientific-discovery
Post by: Bored chemist on 04/09/2021 02:16:49
I had a word with a friend of mine-another guy with 30 something years of actually doing chemistry.
His grasp of maths is a lot better than mine (technically, that's not difficult).
So I asked him whether or not he had ever had occasion to use LaGrangians.
And he asked if I was on about LaGrange points ( The interesting orbits where you put a telescope if you plan to point it at the Sun).
The evidence strongly suggests that chemists don't do LaGrangians.
We don't even understand why we might.
Post by: Colin2B on 04/09/2021 08:46:43
The evidence strongly suggests that chemists don't do LaGrangians.I once went on the ferry to Cork and got talking to a couple on the way. As we approached I asked conversationally for advice on best way to get to our destination. The husband with a broad grin put on his best Irish accent and said “To be sure, I wouldn’t start from here”.
We don't even understand why we might.
One of the marks of a good scientist or engineer that they pick the best tool (or starting point) from the toolkit. Why would anyone use anything but the best tool when in chemistry and biology there are some very sophisticated tools for investigating eg molecules. So I’m with BC.
Post by: Cleonis on 04/09/2021 09:54:46
About Hamilton's stationary action
Hamilton's stationary action is based on the Work-Energy theorem.
(About relation between stationary action and the Work-Energy theorem. Both express physics taking place in terms of Energy, and from both F=ma can be recovered. So we have overwhelming indication that the two are related.)
In the following I will show how to derive Hamilton's stationary action from the Work-Energy theorem. Halfway through this post there is a 7-frame animated GIF that expresses/visualizes all of the mathematical relations.
I start with a derivation of the Work-Energy theorem, to show what elements go into the Work-Energy theorem.
The two relations that constitute the mathematics of the Work-Energy theorem:
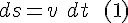
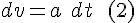
The integral for acceleration from a starting point s0to a final point s .
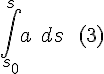
Intermediary step: change of the differential according to (1), with corresponding change of limits.
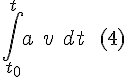
Change the order:
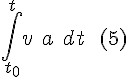
Change of differential according to (2), with corresponding change of limits.
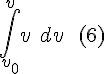
Putting everything together:
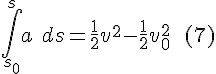
Multiply both sides with m and combine with F=ma to arrive at the work-energy theorem:
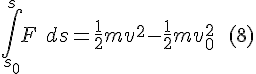
So we should think of the Work-Energy theorem as this:
Start with F=ma, and then take the integral with respect to position of both the left hand side and the right hand side. The left hand side is the integral of force over distance, and the right hand side is the integral of acceleration over distance.
At the end of this post I will return to this way of viewing the Work-Energy theorem.
As we know:
The integral of force over distance is well defined if the difference in potential energy between a point A and a point B is independent from how you moved from A to B. As we know: when that condition is satisfied the force is called a conservative force.
The Work-Energy theorem is applicable when the force involved is a conservative force.
We have:
The integral of force with respect to position is Work done.
Potential energy is defined as the negative of Work done.
In cases where the Work-Energy theorem is applicable the amount of change of kinetic energy matches the amount of change of potential energy.
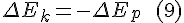
This extends down to infinitisimally small increments
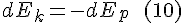
In theory of motion we are accustomed to taking the time derivative
(Also: moving the minus sign inside the differentiation)
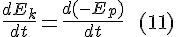
But then: we are not confined to taking the time derivative, taking the derivative with respect to position obtains a valid equation just as well.
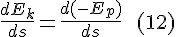
I will refer to (12) as the 'Energy-Position equation' as it evaluates the derivative of the energy with respect to position.
We are now only a single step away from Hamilton's stationary action.
We have that integration is a linear operation
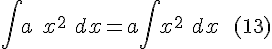
That is: if you have a curve, and you double the slope of that curve, then the value of the integral of that curve doubles with it.
I repeat equation (12)
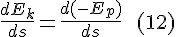
On the basis of (13): the following is valid too:
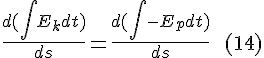
(14) expresses Hamilton's stationary action.
(14) is visualized in the following animated GIF:
(https://i.stack.imgur.com/mc6Gr.gif)
The diagram as a whole sweeps out variation, representing how in calculus of variations variation is applied.
In the upper left subpanel the trajectory of an object is represented. The case represented is that of a linear potential such that an acceleration of 2 meters per second per second is caused.
The start point is at t=-1, the end point is at t=1, the spatial distance is 2 meters.
In the diagram as a whole the color denotes whether the curve relates to kinetic energy or potential energy:
Red: kinetic energy
Green: potential energy
The upper right subpanel and the lower left subpanel show the same curves, the energy as a function of time, given the trajectory in the upper left subpanel. The red curve represents the kinetic energy, the green curve represents the minus potential energy. The curve for the potential energy has been flipped upside down to enable comparison.
The trial trajectory coincides with the true trajectory at the point where the rate of change of kinetic energy matches the rate of change of potential energy.
The diagram shows how the two energies respond to sweeping out variation. The expression for kinetic energy is quadratic, hence the response of the kinetic energy to variation sweep is quadratic. (Differentiation is a linear operation. Doubling the height of the trial trajectory is doubling the velocity along that trial trajectory.)
In this particular example the expression for the potential energy is linear.
As variation is swept out: the kinetic energy responds quadratic to that, and the potential energy responds linear to that.
This difference in response propagates to the values of the respective integrals of the energies.
As we know: Hamilton's action is defined as one integral being subtracted from another integral: the time integral of the kinetic energy minus the time integral of the potential energy. It is only at the point where the trial trajectory coincides with the true trajectory that the two integrals change at the same rate. At that point the derivative of Hamilton's action is zero.
The Euler-Lagrange equation
The Euler-Lagrange equation is a general purpose variational calculus equation. The EL-equation is stated with partial derivatives because there are cases where that is necessary. For classical dynamics the partial derivatives are overkill; the kinetic energy is a function of velocity only, and when the force is a conservative force the potential is a function of position only.
The move from (12) to (14) is the move from the Energy-Position equation to Hamilton's stationary action.
In classical dynamics the derivation of the Euler-Lagrange equation proceeds in the opposite direction, it goes from (14) to (12).
The first step of deriving the Euler-Lagrange equation is to take Hamilton's action, and proceed to take the derivative of it. The variation sweep is variation of position, so derivative with respect to variation and derivative with respect to position are one and the same derivative.
Here is the full EL-equation with the Lagrangian (Ek-Ep) and partial derivatives:
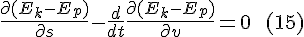
As stated earlier, in classical dynamics the partial derivatives aren't necessary.
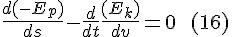
(It's easy to lose track of minus signs here. Anyway: the animated GIF with the visualization corroborates the reasoning, so I'd say it not necessary to worry much about a possible minus sign error.)
We see that the Euler-Lagrange equation takes the derivative of the potential energy with respect to position.
The way that the Euler-Lagrange equation treats the kinetic energy looks complicated, but we know that it must be dimensionally the same as the operation that is performed on the potential energy.
The Euler-Lagrange equation does in fact take the derivative of the kinetic energy with respect to position
This is what the Euler-Lagrange equation does with the kinetic energy:
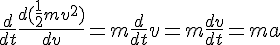
Next, here is what the Energy-Position equation (12) does with the kinetic energy:
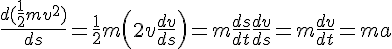
This completes the demonstration that the derivation of the Euler-Lagrange equation (for classical dynamics) is in effect to proceed from (14) to (12).
In classical dynamics the Energy-Position equation (12) and the Euler-Lagrange equation are one and the same equation.
Energy mechanics
The thing that makes the Energy-Position equation so expressive is this: kinetic energy is a quadratic expression, so it takes advantage of Pythagoras' theorem.
If you are treating the physics taking place in terms of force and acceleration then you have to keep track of motion components in the spatial dimensions (when the motion is in 2 or 3 spatial dimensions). With kinetic energy: the expression is already quadratic, so to obtain the resultant kinetic energy you can just add the kinetic energy components together. This means that in effect you can treat the kinetic energy as a scalar. In my opinion the kinetic energy being able to take advantage of Pythagoras' theorem is the biggest windfall in the history of physics.
The Work-Energy theorem is obtained by taking the entire expression F=ma, and integrating it with respect to position.
The Energy-Position equation takes the Work-Energy theorem, and takes the derivative with respect to position.
However, in manipulating the equations actually taking that derivative is postponed.
What you want is to keep using that auxillary variable 'energy' as long as possible, because you can treat kinetic energy as a scalar.
Interpretation of Hamilton's stationary action
Hamilton's stationary action is not about minimization, even though it may appear that it is.
Hamilton's stationary action is about the response of the energy to variation of the trial trajectory.
In the animation above the potential energy changes linear with position. But we can also have a potential energy that increases with the cube of displacement. A cubic expression out-paces a quadratic expression. With a cubic potential the response of the potential energy to variation will outpace the response of the kinetic energy. With a cubic potential (and all higher orders): when the trial trajectory coincides with the true trajectory Hamilton's action reaches a maximum.
It's not about minimum/maximum, it's about the value of the derivative.
When the trial trajectory coincides with the true trajectory the derivative of Hamilton's action is zero.
variational calculus
The equations of theory of motion are differential equations.
In our physics experiments, and in our technology: we can steer how fast objects are moving through space, we have no control over how fast objects are moving through time. Because of that the differential equations of theory of motion are inherently in terms of taking the derivative with respect to time.
In application of variational calculus in theory of motion: taking the derivative is pivoted to taking the derivative with respect to position. Rhetorical question: how is that pivot from time derivative to position derivative accomplished?
As demonstrated above, the Work-Energy theorem is obtained by taking the integral of F=ma with respect to position. This integration stage introduces an auxillary quantity, which we call 'Energy'. To recover F=ma we take the derivative with respect to position.
This auxillary quantity 'Energy' has among its properties the following: it has no intrinsic zero point. There is no intrinsic point of zero potential energy; potential energy can be defined only in terms of difference of potential energy between points A and B. Whenever you do a calculation you need to set some point as zero potential, but the choice of zero point is arbitrary, you just need to apply it consistently.
Presumably this way of setting up for variational approach can be generalized. Presumably the process will involve doing an integration that creates an auxillary quantity. This auxillary quantity will then not have an intrinsic zero point, making the choice of zero point arbitrary.
Generally:
The pivot from differential form to variational form does not involve physics; the pivot is purely application of mathematics.
The information above is also available on my website, with better diagrams. My forum profile has the link to my website. (This is my first post, so I suppose I won't be permitted to add links)
The treatement of Hamilton's stationary action is in the section 'variational calculus'.
The diagrams on my website are interactive. There is a main slider that executes global variation sweep, and there are additional sliders for local variation. As you sweep out variation the diagram shows how that propagates to the curves for the respective energies, and to Hamiltons action. The following three cases are implemented: linear potential, quadratic potential (Hooke's law), cubic potential.
Post by: Eternal Student on 04/09/2021 16:55:13
@Cleonis
I don't have much time to respond now. You have presented some information about the derivation of Hamiltonian and Lagrangian mechanics for some simple mechanical systems.
It looks perfectly sensible and interesting but it isn't taliored to respond or relate to comments and discussions that were already in this thread. I'm hoping that you will understand that some of us will remain uncertain about what it's purpose was until you have made some more posts and interacted with other people.
Welcome and thanks for your time. I will read your post more thoroughly later.
Best Wishes.
Post by: Cleonis on 04/09/2021 17:45:39
I'm hoping that you will understand that some of us will remain uncertain about what it's purpose was until you have made some more posts and interacted with other people.
Of course, these things take some time to build.
I haven't figured out the reply flow of this forum. At the top and the bottom of each page there is a black 'Reply' button, which I suppose starts a reply to the first post of the thread (the button doesn't say what it replies to)
Then there is the feature I'm using now, which by the looks of it is called 'Quick-Reply', and it is not clear to me how far the functionality of this 'Quick-Reply' extends.
I have looked for a 'How to use' for this forum, but I haven't found it.
(Well, I just clicked the button for the 'preview' of the Quick-Reply, which opened all the rows of formatting buttons. So I guess the Quick-Reply option is the actual reply flow of this forum.)
Post by: Eternal Student on 04/09/2021 23:29:09
At the top and the bottom of each page there is a black 'Reply' button, which I suppose starts a reply to the first post of the thread (the button doesn't say what it replies to)Yes there's a whole lot of things that aren't clear in this forum.
Personally I would NOT use the "Quick Reply" feature. Just use the main "Reply" button. Why? Because this website has a habit of timing you out and making you lose everything you've typed. If this ever happens to you, the "back" button on your browser will usually get you back to a point where you can at least see your own work and "copy it". However, if you used the quick reply feature then whatever you've typed seems to be gone and never coming back to you.
The general flow of this forum: Nothing gets indented, nothing looks like a reply aimed at only one person. Your reply just goes at the bottom (i.e. in chronological order). If you want to make it clear you were addressing a point made by one person then write @Cleonis (put their username, not your own) or else start a reply and THEN grab a "quote" from something the other person wrote. You've obviously used this since you put some of my text in a quote box successfully.
The "preview" button is ever so useful to check that what you've written looks sensible. If it looks sensible to you, we will probably be able to follow it.
- - - - - - - - - - - -
Anyway, I've had a bit more time to read through your previous post. It's obviously very good and the LaTex must have taken you some time to produce. Well done. Not everyone will like it because there's Maths in it but never mind, you can't please them all.
I made a comment earlier that for simple mechanical systems, it's not too difficult to see that a Lagrangian can be constructed and a least action (or stationary action) principle would apply. (You're not expected to have read all of this thread). The wider context of my original post is - why do Physicist's think that a Lagrangian and a least action principle would be a suitable way to describe every system we might want to study? I accept that it is suitable to describe simple mechanical systems in which you might expect Newtonian mechanics to apply. However, why do Physicist's try and use Lagrangian mechanics almost everywhere and for almost everything?
Examples:
1. Lagrangian formulation of classical field theory. https://en.wikipedia.org/wiki/Lagrangian_(field_theory).
Here fields posses certain energies and the Lagrangian is not exactly K-V (Kinetic - Potential) but something slightly more complicated and abstract. However, it is a generalisation of Lagrangian mechanics. The fundamental laws are expected to appear from the Euler-Lagrange equations given a suitable Lagrangian to start with.
2. The Hilbert-Einstein action from which the Einstein Field Equations can be derived from a least action principle. This was developed AFTER the theory of General Relativity was published, so it is not needed. For some reason it was felt that Lagrangian mechanics and a least action principle would be the way that all physical systems should be modeled and all physical laws would then be determined from the Euler-Lagrange equations that appear.
3. Noether's theorem. This says nothing about general physical systems, it only concerns systems that are described with a Lagrangian. Why would we think all systems can be described with a Lagrangian and a stationary action principle would apply?
I don't know and if you have any ideas, I'd like to hear them.
What proof exists that all physical systems can be described by a Lagrangian and a stationary action principle would apply?
Also, this is NOT my forum. You are free to have a side-line discussion right here on a related topic if you wish. I certainly don't mind and I'll probably join in. Unlike many other forums, this sort of thing happens often. However, common sense rules the day and if a discussion wanders too far then someone (possibly a moderator) will suggest starting a new thread or else just split the two threads anyway.
Best Wishes.
Post by: Cleonis on 05/09/2021 07:30:23
some of us will remain uncertain about what it's purpose was until you have made some more posts and interacted with other people.
In my first post I opted to present a self-contained exposition of the nature of Hamilton's stationary action.
Let me write now about my purpose in general, and my goals for Energy mechanics specifically.
My overall purpose is to clarify and to unify. I am always on the lookout for interconnections between adjacent areas of physics.
I use the name 'Energy mechanics' as an umbrella term for all forms of expressing physics taking place in terms of kinetic and potential energy. So that covers the Work-Energy theorem to Hamiltonian mechanics and everything in between.
So back when I was studying physics, when I was introduced to Hamilton's stationary action, the same questions arose in me that arise in every other student has: "How can this be?" "Why does this hold good?" Over the years I kept returning to it, searching the internet for new publications, with perhaps new clues.
I noticed that the expression 'stationary action' was already used by William Rowan Hamilton himself. I surmise that Hamilton was aware that the point where the derivative of Hamilton's action is zero can be either a minimum or a maximum. Whether it is minimum or maximum doesn't make it to the Euler-Lagrange equation.
The derivation of the Euler-Lagrange equation boils things down to what is necessary to obtain the equation of motion. The Euler-Lagrange equation is agnostic as to whether the action is at a minimum or a maximum.
So: from the start (the introduction by William Rowan Hamilton) there was a strong indication that Hamilton's stationary action is not about minimizing.
Rather, if you have a curve that goes from sloping one way to sloping the other way, and the point you need to identify is the point where the derivative is zero, then at the point you have identified you are also at an extremum of that function.
As stated in one of the opening paragraphs of my post #26 in this thread: Hamilton's stationary action and the Work-Energy theorem have the following in common:
- both describe physics taking place in terms of kinetic and potential energy
- from both F=ma can be recovered.
To explore that connection I started creating interactive diagrams, similar to the one in post #26, using the interactive diagrams as a lab. I found my way around by creating different versions of the interactive diagram. It was the interactive diagrams that allowed me to see the connection. After that I wrote the narrative in terms of mathematical formulas.
The traditional way of presenting Hamilton's stationary action is to start with presenting Hamilton's stationary action, and then work back to show that F=ma can be recovered from it.
In my post #26 I arrive at Hamilton's stationary action in all forward steps, which I think is a much cleaner way.
I believe with this exposition in forward steps the question "Why does Hamilton's stationary action hold good?" is answered.
I'm in the process of getting this information to wider attention.
Three weeks ago I notified Professor Steven Strogatz of the page on my website with the interactive diagrams, and he tweeted the link.
(Being a new contributor here I cannot post links yet, so I give the link to the tweet with spaces in it)
Mod edit: please don’t try to circumvent the link limitations until you are allowed to post links. Thank you
Post by: Cleonis on 05/09/2021 07:54:58
You have presented some information about the derivation of Hamiltonian and Lagrangian mechanics for some simple mechanical systems.
My thoughts on that are as follows:
The derivation presented is for the case of motion in a single spatial dimension. I take it as granted that the discussion generalizes to motion in 2 and 3 spatial dimensions.
The derivation presented uses cartesian coordinates, but it is not dependent on using cartesian coordinates; the reasoning is applicable as well when using generalized coordinates.
The derivation presented only requires that the potential is well defined (the force is a conservative force). Other than that the potential can be any function of position.
Of course, many different actions have been formulated in addition to Hamilton's action, to accommodate specifics of physics taking place.
I expect that these various forms of Lagrangian mechanics have the following in common: that the underlying reason that the stationary action of that form of Lagrangian mechanics holds good is the same for all.
That is, my expectation is that the structue of the derivation presented here generalizes to all forms of Lagrangian mechanics.
Post by: Cleonis on 05/09/2021 08:17:50
What proof exists that all physical systems can be described by a Lagrangian and a stationary action principle would apply?
I refer to the process of converting from differential calculus form to variational calculus form as 'pivoting'; to pivot from derivative with respect to time to derivative with respect to position.
In my post #26 the pivot is the one for classical mechanics. I think it would be very interesting to see if the underlying structure of that process can be generalized.
To explore that we need to examine the relation between differential calculus and variational calculus.
As is well known, the problem that started the development of variational calculus was the Brachistochrone problem.
When Johann Bernoulli had presented the Brachistochrone problem to the mathematicians of the time Jacob Bernoulli was among the few who was able to find the solution independently. The treatment by Jacob Bernoulli is in the Acta Eruditorum, May 1697, pp. 211-217
Jacob opens his treatment with an observation concerning the fact that the curve that is sought is a minimum curve.
(https://i.stack.imgur.com/5eSxk.png)
Quote
Lemma. Let ACEDB be the desired curve along which a heavy point falls from A to B in the shortest time, and let C and D be two points on it as close together as we like. Then the segment of arc CED is among all segments of arc with C and D as end points the segment that a heavy point falling from A traverses in the shortest time. Indeed, if another segment of arc CFD were traversed in a shorter time, then the point would move along ACFDB in a shorter time than along ACEDB, which is contrary to our supposition.
Jacob's lemma generalizes to all cases where the curve that you want to find is an extremum; either a maximum or a minimum. If the evaluation is an extremum for the entire curve, then it is also an extremum for any sub-section of the curve, down to infinitisimally short subsections.
The Euler-Lagrange equation is the most general equation to handle variational calculus. The Euler-Lagrange equation takes any problem that is stated in variational form, and converts it to differential form.
We have that physical systems are represented with differential equations.
Conjecture:
The nature of the mathematical relation between differential calculus and variational calculus is such that any system that can be represented in differential calculus form can also be represented in variational calculus form (using the Euler-Lagrange equation to convert back to differential calculus form).
If such a general conjecture can be proved then that would constitute a proof that mathematically any physical system that can be represented with differential calculus form can also be represented with variational calculus form.
Post by: Eternal Student on 06/09/2021 01:20:42
I've been busy as of late and not had much time to read through long posts, sorry.
I'm steadily getting through some of what you've written and I'm very grateful for the time you've spent.
Here's a minor thing I've noticed:
That is: if you have a curve, and you double the slope of that curve, then the value of the integral of that curve doubles with it.Equation (13) was acceptable (where a = constant) but this paraphrasing of the result is poor.
y = f(x) and y = 2f(x) + 3 are two curves. One curve has double the slope of the other but an integral of these curves will not produce results where one is double the other.
- - - - - - - - - - -
I noticed that the expression 'stationary action' was already used by William Rowan Hamilton himself. I surmise that Hamilton was aware that the point where the derivative of Hamilton's action is zero can be either a minimum or a maximum. Whether it is minimum or maximum doesn't make it to the Euler-Lagrange equation.I agree. However, if a function F obtains a local maxima then the function -F (or similar functions like 270-F if you want to retain a positive value throughout) will obtain a local minima. It's therefore acceptable to say that nature minimisies something if it maximises another thing. However, I completely agree that it is only that there is something that becomes stationary that is important.
The derivation of the Euler-Lagrange equation boils things down to what is necessary to obtain the equation of motion. The Euler-Lagrange equation is agnostic as to whether the action is at a minimum or a maximum.
- - - - - - - -
In my post #26 I arrive at Hamilton's stationary action in all forward steps, which I think is a much cleaner way.You have been using ds and derivatives
I believe with this exposition in forward steps the question "Why does Hamilton's stationary action hold good?" is answered.
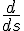where s was position. This is subtly different from a variation of path taken. Looking at your original post you said the following: The diagram as a whole sweeps out variation, representing how in calculus of variations variation is applied. and you have produced a nice animated gif. However, all of the paths looked like parabolic paths and only the height obtained was varied. There are stranger paths that could be considered.
I'll need more time to look back through exactly what was done but it's a bit too late for me to concentrate at the moment.
- - - - - - - - - - -
Of course, many different actions have been formulated in addition to Hamilton's action, to accommodate specifics of physics taking place.The derivation you have provided rested heavily upon what you are describing as "energy mechanics". It made various assumptions about energy that are all perfectly reasonable in simple mechanical systems. However, "potential energy" is not always well defined in some situations (e.g. gravitational potential energy is not always well defined in General relativity).
I expect that these various forms of Lagrangian mechanics have the following in common: that the underlying reason that the stationary action of that form of Lagrangian mechanics holds good is the same for all.
That is, my expectation is that the structue of the derivation presented here generalizes to all forms of Lagrangian mechanics.
Don't get me wrong - It seems that Lagrangian mechanics does generalise to cover various situations and I like your statement of expectation.
---- It's getting far too late for me to concentrate. I'm signing off and will look through your last post later. Best Wishes, thank you for your time and good luck with your website etc.
Post by: yor_on on 06/09/2021 15:22:31
https://en.wikipedia.org/wiki/Fermat%27s_principle
=
Thinking of it, it always struck me as strange that transformations doesn't 'cost'. As far as I've seen that's the whole idea of conservation of energy when describing a 'isolated system' transforming. But to me something should be lost in each step, the end result becoming heat. If it transforms something must change. The only definition I know of there is 'useful energy' relative 'non useful energy'. JP (physicist) called it a 'coin of exchange', energy, and that one stuck in my head.
Post by: Eternal Student on 06/09/2021 21:52:09
I've finished reading through Cleonis' last post.
I refer to the process of converting from differential calculus form to variational calculus form as 'pivoting'; to pivot from derivative with respect to time to derivative with respect to position.Which is not quite what the variational calculus is about. The variations involve small adjustments of entire paths rather than small adjustments of 1 variable like position.
The Euler-Lagrange equation is the most general equation to handle variational calculus. The Euler-Lagrange equation takes any problem that is stated in variational form, and converts it to differential form.Agreed. I'd rather the phrase "to handle" was adjusted. The E-L equations are the most general differential equations that follow (and are necessarily satisfied) from the variational calculus.
Conjecture:Agreed. Such a conjecture and it's formal proof is exactly what is required. It would be a big step forward.
The nature of the mathematical relation between differential calculus and variational calculus is such that any system that can be represented in differential calculus form can also be represented in variational calculus form (using the Euler-Lagrange equation to convert back to differential calculus form).
If such a general conjecture can be proved then that would constitute a proof that mathematically any physical system that can be represented with differential calculus form can also be represented with variational calculus form.
(Sadly, there may still be some systems we wish to study but differential equations linking some variables together are not present).
- - - - - - - -
@yor_on,
Yes, Fermat's principle is another good example for a stationary action principle.
The only definition I know of there is 'useful energy' relative 'non useful energy'.All of this section also sounds reasonable. The sort of thing your describing is often called "Free Energy" or "Gibbs Free Energy". The "something lost" or price to be paid during a transformation is the entropy change.
Best Wishes to everyone.
Post by: Cleonis on 06/09/2021 22:41:11
[...] animated gif. However, all of the paths looked like parabolic paths and only the height obtained was varied. There are stranger paths that could be considered.
Indeed the total variation space can be thought of as a multi-dimensional space. And in the limit of an infinite amount of points along the trial trajectory that is an infinite-dimensional space.
For variational calculus Jacob's lemma is crucial, which is why I presented Jacob's lemma in my post #32 of this thread. I repeat the diagram, I don't repeat the exposition here, please see post #32
(https://i.stack.imgur.com/5eSxk.png)
(I refer to it as Jacob's lemma (it was introduced by Jacob Bernoulli) because calling it Bernoulli's lemma would be ambiguous.)
Hamilton's action evaluates to a single value. How does it come about that while the variation has in principle infinite-dimensional freedom, that freedom can somehow be narrowed down to a single value: the value of Hamilton's action.
Start with the total curve, the solution to the variational problem.
The total curve satisfies the minimum/maximum condition of the problem.
It's the global solution, we proceed to treat that curve as a global fixed curve. So we can take any subsection along that curve, and treat the two end points of that subsection as fixed points. The curve between those two points satisfies the minimum/maximum condition of the problem.
When the global solution satisfies the minimum/maximum condition of the problem then all subsections of the curve satisfy the minimum/maximum condition of the problem. This is valid down to infinitisimally small subsections.
Preetum Nakkiran has demonstrated that the Euler-Lagrange equation can also be derived using only infinitissimally short subsections.
Being an new member I cannot yet post a link, so I give the URl with spaces in it.
To make such a derivation work: the setup is such that it is independent of where along the curve the infinitissimally short subsection is located. That way the reasoning is simultaneously valid for the curve as a whole.
On each infinitissimally short subsection the variation space is down to a single parameter.
We can think of the global variation as a concatenation of local infinitissimal variations.
It is because of that concatenation that the evaluation of the trial trajectory can be meaningully narrowed down to a single number: Hamilton's action.
The derivative of Hamilton's action is zero when it is zero along every subsection of the global trajectory.
The interactive diagrams on my website are much richer than the animated gif. These interactive diagrams have additional sliders that execute local variation, allowing the visitor to explore the effect of local variation.
Numerical analysis
Another way of looking at this issue is by considering how numerical analysis of variational calculus must be implemented as a computer algoritm.
Numerical analysis implementation of variational calculus is as follows: time is divided in small increments. Then there is an iterative calculation: In each step the algorithm evaluates the middle point of a triplet of points, advancing one time increment each step. In each step the middle point is adjusted relative to its directly adjacent points, to make that middle point satisfy the extremum condition with respect to the current positions of its adjacent points:
t0, t1, t2
t1, t2, t3
t2, t3, t4
And so on.
When the last point is reached the iteration start again with the first point.
The simplest seed for the iterative calculation is a flat line. The iteration can start with any seed.
Over each iteration the trial trajectory shifts towards the true trajectory.
Over a sufficiently large number of iterations the trial trajectory converges to the true trajectory to within any desired level of computational accuracy. So: the numerical analysis implementation arrives at satisfying the extremum condition globally by iteration of evaluating the extremum condition locally.
And of course: the smaller the time increments the higher the level of computational accuracy.
So that is how implementation of variational calculus as a computer algorithm handles the dimensionality of the variation space.
Post by: Cleonis on 07/09/2021 21:16:34
[...] what the variational calculus is about. The variations involve small adjustments of entire paths rather than small adjustments of 1 variable like position.
General statement:
The validity of Hamilton's stationary action is independent of what variational calculus is about.
While discussing what variational calculus is about is interesting and relevant on its own merit, that discussion is not necessary in order to discuss Hamilton's stationary action.
We have that in classical mechanics the Euler-Lagrange equation with the Lagrangian (Ek-Ep) is a differential equation that takes the derivative of the energy with respect to position.
As we know: in classical mechanics the derivation of the Euler-Lagrange equation starts with setting up the derivative of Hamilton's action with respect to variation. And then in the course of the derivation the relation between the derivative with respect to variation and the derivative with respect to position is worked out.
The end result is that the Euler-Lagrange equation with the Lagrangian (Ek-Ep) inserted takes the derivative of the energy with respect to position.
This demonstrates that in classical mechanics it is valid to narrow down what is varied about the entire path to variation of position. Proof by contradiction: if that narrowing would not be valid then the derivation of the Euler-Lagrange equation itself would be invalid.
In the course of the derivation of the Euler-Lagrange equation the derivative with respect to variation is converted to the derivative with respect to position. That happens anyway. Therefore it is without loss of generality that Hamilton's stationary action can from the start be stated in terms of derivative with respect to position.
Post by: yor_on on 08/09/2021 08:47:45
=
It's very hard to define, what I'm thinking of here. But you could see it as a question of what defines reality. Abstractions or grains.
Post by: Eternal Student on 09/09/2021 21:08:43
We have that in classical mechanics the Euler-Lagrange equation with the Lagrangian (Ek-Ep) is a differential equation that takes the derivative of the energy with respect to position.Yes.
It also takes derivatives with respect to time and a derived variable
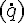, if that matters.As we know: in classical mechanics the derivation of the Euler-Lagrange equation starts with setting up the derivative of Hamilton's action with respect to variation.Yes.
And then in the course of the derivation the relation between the derivative with respect to variation and the derivative with respect to position is worked out.I'm concerned about how you phrased this.
Let's write
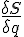for the quantity usually referred to as the derivative of the action, S, with respect to "variation".It's fair to say that the E-L equations follow from
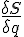= 0 but they do not provide an expression that relates 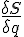to a more conventional real derivative like 
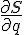where S is regarded as a function (not a functional) and q is a real valued variable (not a function).The E-L equations provide 2nd order differential equations that show the relation between
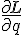and 
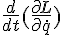both of which are conventional real derivatives (or partial derivatives).Hamilton's stationary action principle states that δS = 0 and sometimes, for convenience, we could write this in pseudo-derivative form (or "functional derivative form")
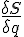= 0 and call this the derivative of S (the action) with respect to variation. However S and therefore δS were always understood to be functionals and not real valued functions of a single variable. So that 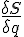does not represent any conventional derivative.- - - - - - - - -
This demonstrates that in classical mechanics it is valid to narrow down what is varied about the entire path to variation of position.Yes, seems perfectly sensible. Although, variation of position is not quite the same as taking a derivative with respect to position. My idea of variation of position is that at least some point(s) visited by the object along the path are in my control. I can vary those and see what the overall effect will be. Meanwhile, a derivative
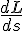involves a limit of ratios of small changes but none of those changes are in my control. The function L is required to be a function of s and then 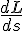is entirely determined, I don't have control or the ability to vary anything.Here's what you (Cleonis) said in an earlier post: (Screenshot should follow)
screen-A.JPGThe equation (14) you have written is correct but it tells me nothing about what I can vary. It implies that everything is already a function of s.
Proof by contradiction: if that narrowing would not be valid then the derivation of the Euler-Lagrange equation itself would be invalid.I won't dispute that variation in the path can be reduced to some variation in position(s) taken by the object during the path. It's just that I don't see variation in position as anything especially related to a derivative with respect to a displacement variable, s.
The derivations of the E-L equations that I have seen do not involve taking derivatives with respect to displacement. Instead some variation in position(s) is permitted by another method. An arbitrary function h(q) is introduced and we consider a family of curves of the form y(q) + ε h(q) where ε is an arbitary real variable. We reduce the problem down to one variable by allowing ε to be the only thing that varies. Then we can use single variable calculus to make progress.
There is obviously a link between reducing the problem to 1 variable, ε, and reducing the problem to an adjustment of some position(s) that the object would take during the path. That link is that h(q) is a perturbation from the ideal path. We have control over ξ and so we have some control over a variation in some positions taken by the object during the path.
In the course of the derivation of the Euler-Lagrange equation the derivative with respect to variation is converted to the derivative with respect to position. That happens anyway. Therefore it is without loss of generality that Hamilton's stationary action can from the start be stated in terms of derivative with respect to position.The "derivative with respect to variation" is not a conventional derivative as mentioned earlier. It is indicative of a concept or principle. This concept seems to be converted into several conventional real derivatives, there are derivatives with respect to position, time and a derived variable appearing in the Euler-Lagrange equations.
Your "pivoting" process does seem to be a conventional process of changing variables in calculus (either in derivatives or intergrals), it is not obviously connected with allowing an arbitary variation of anything about the path taken. (Perhaps I'm just missing something).
- - - - - - - - -
Summary: I like what you've said and I'm very grateful for your time. There is obviously a connection between considering arbitrary variation in path taken by a system and just a single variation in some element of position taken by an object at some fixed time during the path. This was illustrated well in your post about numerical techniques for solving variational problems. Well done and thanks etc.
It's still a bit of a jump or conjecture to get from here to stating Hamilton's action principle in terms of an ordinary derivative with respect to position.
Best Wishes.
Late editing: Just trying to insert the screenshot of the old post.
Post by: Cleonis on 09/09/2021 22:27:44
There is obviously a connection between considering arbitrary variation in path taken by a system and just a single variation in some element of position taken by an object at some fixed time during the path. This was illustrated well in your post about numerical techniques for solving variational problems.
Numerical analysis implementation
In the course of developing various diagrams I got to think a lot about numerical analysis implementation of variational calculus.
I expect that numerical analysis implementation will be a fruitful way of investigating and demonstrating the relation between differential calculus and variational calculus.
I repeat the link to Preetum Nakkiran's derivation of the Euler-Lagrange equation (classical mechanics). (Spaces inserted; I can't post links yet) As stated before, Preetum uses local reasoning.
Differential calculus
In numerical analysis implementation of differential calculus the smallest unit of evaluation is a pair of points. As we know, the simplest implementation is Euler integration. The integration proceeds from point to point. The current acceleration gives the current velocity, the current velocity gives the distance that will be traversed in moving from the current point to the next point. Rinse and repeat.
Variational calculus
In numerical analysis implementation of variational calculus the smallest unit of evaluation is a triplet of points.
t0, t1, t2
t1, t2, t3
t2, t3, t4
In each consecutive triplet-of-points evaluation the outer points of the triplet are treated as fixed.
For the case of classical mechanics:
As you execute variation of the middle point Hamilton's action is affected in two ways:
1) The integral of the potential energy is a function of the position of the middle point.
2) The triplet t0, t1, t2 has the following two subsections
t0, t1 and t1, t2
Lowering the position of the middle point has as effect:
- the velocity along interval t0, t1 is lowered
- the velocity along interval t1, t2 is raised.
Raising the position of the middle point has the opposite effect.
Schematically:
Differential calculus: smallest unit of evaluation: a pair of points
Variational calculus: smallest unit of evaluation: a triplet of points
The derivation of the Euler-Lagrange equation for the general case demonstrates that any problem stated in variational form can be converted to differential form.
Differential calculus (pair-of-points calculus) has a simpler structure than variational calculus (triplet-of-points calculus)
Conversion of differential form to variational form is referred to as an 'inverse problem'.
Post by: Cleonis on 12/09/2021 16:33:22
There is obviously a connection between considering arbitrary variation in path taken by a system and just a single variation in some element of position taken by an object at some fixed time during the path.
In the case of differential calculus the smallest unit of operation is a pair of points. Geometrically: you take a pair of points on the horizontal axis, a and (a + h), and then you obtain the following ratio:
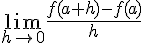
The diagram below represents the smallest unit of operation of variational calculus. In numerical analysis implementation this is the unit of operation (concatenated in iteration cycles as necessary).
(https://i.stack.imgur.com/pvC6C.png)
Horizontal axis: time
Vertical axis: position
Variational calculus: numerical analysis implementation
To find the true trajectory:
- divide the total time in sub-intervals
- adjust the position of the points along the trajectory until all points satisfy the stationary criterium. (Each point evaluated with respect to its adjacent points.)
In the limit of making the time increment infinitely small one obtains the variational counterpart of taking a derivative.
Disclaimer:
This is not writen as an exhaustive derivation. Rather, it is a demonstration of the nature of Hamilton's action. The exposition below is intended to serve as corroborating evidence.
The following exposition is in notation specific for problems in mechanics.
t for 'time'
s for 'position'
v for 'velocity'
a for 'acceleration'
However, the structure of the derivation is not specific to dynamics; it generalizes to all of variational calculus.
S for Hamilton's action
Sk for the kinetic energy component of Hamilton's action
Sp for the potential energy component of Hamilton's action
In order to proceed an auxillary quantity is necessary.
We are trying to find the equation of motion for the trajectory; an equation of motion gives position as a function of time. But in variational calculus what is varied is the position coordinate. Therefore we need a function that assigns a value to each point along the trajectory, allowing us to differentiate that value with respect to position.
In classical mechanics this auxillary quantity function is created by integrating F=ma with respect to position, resulting in the Work-Energy theorem:
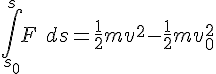
The Work-Energy theorem states how potential energy and kinetic energy are related.
We have: potential energy is a function of position; kinetic energy is a function of velocity.
In the diagram δs represents an infinitisimally small variation of position. The potential energy and the kinetic energy each respond to that variation, each responding differently to δs .
The response of the potential energy component of Hamilton's action:
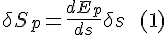
The response of the kinetic energy component of Hamilton's action:
On both side of t2 the velocity changes; one side increases, the other side decreases.
Before the change:
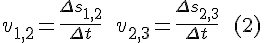
After adding δs :
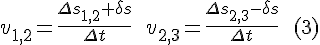
The changes of the velocities:
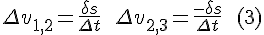
The change of the kinetic energy component of Hamilton's action:
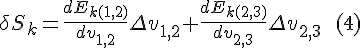
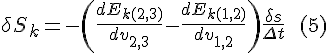
The total time is divided in equal length sub-intervals, so the move from interval (1,2) to the adjacent (2,3) can be rearranged to the form of taking a time derivative:
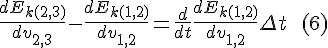
Combining (5) and (6) we obtain an expression for the change of the kinetic energy component of Hamilton's action as a function of δs:
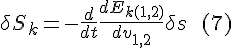
Combining the two responses:
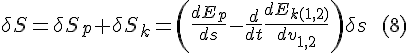
The variation δs, having served its purpose, can now be eliminated. The stationary-in-response-to-variation condition is satisfied when the following is satisfied:
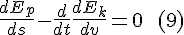
As we know, in classical mechanics the kinetic energy term in (9 ) simplifies to mass times acceleration:
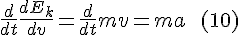
The above derivation explains why F=ma can be recovered from Hamilton's stationary action.
The Work-Energy theorem is derived from F=ma
Hamilton's stationary action is a corollary of the Work-Energy theorem
Numerical analysis implementation
Numerical analysis implementation is where the rubber meets the road. If variational calculus is implemented numerically the algorithm will proceed according to the diagram. Take a triplet t1, t2, t3, adjust the position of the middle point, then move up one time increment: t2, t3,t4. When you have reached the end point: cycle again over the entire time interval. Over multiple iterations the set of points will converge onto the true trajectory. (Alternatively you could randomize the choice of triplet to evaluate. The algorithm will of course converge onto the same true trajectory.)
(There are Java simulations available on the website of Edwin Taylor where you can actually watch iteration cycles converge rapidly onto the true trajectory. (I don't know whether those simulations still run on recent versions of the Java Virtual Machine.))
Post by: Eternal Student on 12/09/2021 20:23:47
Minor printing / typing error: In equations (7) and (8 ) you have written
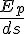where the conventional derivative 
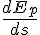should be printed. This doesn't change the essence of what you have done, it's just a printing error.Best Wishes.
Post by: Cleonis on 12/09/2021 21:13:31
typing error
Yeah, that was a typing error. Then I noticed I had accidentally used (7) twice, so I corrected that too.
More generally: in post #41 the terms Ek and Ep are intended as referring to a value that is a function of the trajectory. I thought about defining some letter of the greek alphabet to represent the trajectory, τ for example, to give indication/reminder that the energy is a function of τ.
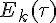
So I'm not happy with my notation here, but I'm not sure whether our notation conventions support something better.
Post by: Cleonis on 15/09/2021 20:02:52
I repeat the diagram from post #41
(https://i.stack.imgur.com/pvC6C.png)
The diagram illustrates the relation between variational calculus and differential calculus.
The general derivation of Euler-Lagrange equation shows that any problem that can be stated in variational form can be restated in differential calculus form.
The triplet of points of the unit of operation of variational calculus can be thought of as two pairs of points (with the middle point as shared point).
In numerical analysis implementation of variational calculus you start with a seed, and then you iterate. I think it is worthwhile to examine closer how that works out.
The cumulative effect of all the iterations is that the trajectory that you are converging onto satisfies the stationary action criterium along the whole trajectory. In the end result: the convergence of each point along the trajectory has been influenced by the convergences of all the other points along the trajectory.
The points along the trajectory are concatenated, so over the course of the iterations adjustment of any single point propagates to the neighbours of that point; to the neighbours of those neighbours, all the way out.
Because of this propagation-to-neighbours, along the chain, a strictly local evaluation of each unit of operation is sufficient as unit of iteration.
The variation of the unit of operation is linear variation only.
We see the theme of narrowing to linear variation also in the standard derivation of the Euler-Lagrange equation. At the start it is stated that the variation is allowed to be any polynomial. (We have of course that any function can be represented as a Taylor series polynomial.)
At the next stage in the derivation the following is argued:
The variation is taken to be infinitisimally small, therefore when considering the Taylor series expansion all terms quadratic and higher can be dropped.
Now, after dropping quadratic and higher terms what remains is a single linear term; the variation space has been narrowed down to linear variation only.
So we have: in variational calculus you can represent the variation with any polynomial that you want, as long as you agree to drop all terms quadratic and higher.
Hamilton's action is defined as an integral of the Lagrangian (
)
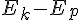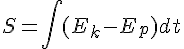
So: what is that integral doing there?
The integration serves to conglomorate the set of all infinitisimal units of variation. That is how Hamilton's action assigns a single number to each trial trajectory; that single number is the conglomoration of all of the constituent infinitisimal variational units.
The integration in the definition of Hamilton's action isn't actually doing anything.
The first step of deriving the Euler-Lagrange equation is the step that does the actual job. That first step is to set up the derivative of the action.
Over the course of deriving the Euler-Lagrange equation the integration is removed. (It has to be removed because it isn't doing anything.) What is retained throughout the course of deriving the Euler-Lagrange equation is that first step: taking the derivative with respect to position.
The energy-position equation
The Work-Energy theorem is applicable when there is a well defined potential energy.
It follows from the Work-Energy theorem that the rate of change of kinetic energy will be equal to the rate of change of potential energy, with opposite sign
Hence the following equation, that I refer to as 'the energy-position equation':
As stated earlier in post #26, in classical mechanics it isn't necessary to write the Euler-Lagrange equation with partial derivatives because the potential energy is a function of position only, and the kinetic energy is a function of velocity only.
The way the Euler-Lagrange equation processes the kinetic energy looks different from that of the energy-position equation, but it is the same.
This is what the Euler-Lagrange equation does with the kinetic energy:
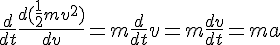
Next, here is what the Energy-Position equation does with the kinetic energy:
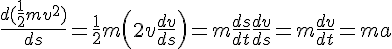
Both evaluate to
because they are actually the same expression.Post by: Eternal Student on 16/09/2021 01:04:08
should be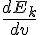 
. It is just a typing error, it has no effect on the remainder of the post.- - - - - - - - - - - - -
You are spending time to demonstrate something that is reasonably well established for classical mechanics involving one particle moving in a potential V(s).
1. It might be harder to make the same steps for multiple particles.
Consider, for example, your equation (1) which follows from the Work-Energy theorem.
The Work-Energy theorem is often stated in this form:
= 
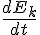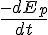showing derivatives with respect to time.For multi-particle systems this is assumed to be well defined (the Energies are assumed to be differentiable functions of time).
However, for a multi-particle system, getting from here to your version of the equation, which you call the Energy-Position equation is non-trivial. It requires a change of variables for the derivatives.
We have
= 
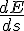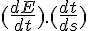provided all the derivatives on the R.H.S. exist [Change of variables equation]
where E = one of the energies of interest Ek or Ep ; s = position of one particle; t= time.There are some systems where our chosen particle could be at rest for a moment during the path of evolution of our system. (* See below for an example).
Then it's velocity = 0 =
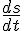, so that 
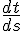→ ∞ and so the change of variables formula doesn't define the quantity 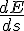when our chosen particle is at rest.This wasn't a problem for a one particle system, since we know in advance that the kinetic energy will remain 0 when the velocity is 0. Similarly we know that if the particle was at rest then the potential energy doesn't change either. So we are not solely dependant on the change of variables formula stated above, we can establish the existence of the derivative
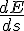by more direct methods.However, these assumptions are not valid for a multi-particle system. There could be some other particles in the system that are moving while our chosen particle remains at rest and this could change the total potential energies. Indeed, if the motion of those other particles is changing, then the kinetic energies change as well.
To paraphrase this, it is not obvious that we can identify a single particle in a multi-particle and it's corresponding position variable, s, such that the work energy theorem can be changed from a derivative with respect to time into a derivative with respect to that position variable.
* An example of a system where one particle remains at rest for quite a lot of the time during the evolution of the system is given by a spring or "slinky" when it is extended and then dropped. See this video if you wish:
2. I've already said enough and I'll sign off for now.
Best Wishes.
Post by: Cleonis on 16/09/2021 20:52:58
However, for a multi-particle system, getting from here to your version of the equation, which you call the Energy-Position equation is non-trivial. It requires a change of variables for the derivatives.
The thrust of your original question, in post #1 was:
"Why do we see many instances of an action formulation hold good?"
I responded by submitting a discusson of Hamilton's stationary action, showing why Hamilton's stationary action holds good, and I submitted that making Hamilton's stationary action transparent provides insight for the purpose of making all action formulations transparent.
We have: in classical mechanics context Lagrangian mechanics is applied in multiple-particle cases. It's a solved problem.
We have:
- The question why Hamilton's stationary action holds good
- The question of how to apply Lagrangian mechanics in multiple-particle cases
Those two are independent questions.
I submit that the following two equations are mathematically equivalent.
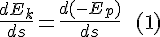
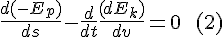
That is:
I submit the following reasoning:
- (1) and (2) are mathematically equivalent.
- (2), the Euler-Lagrange equation (for classical mechanics), is regarded as expressing the foundation of Lagrangian mechanics.
- Since (1) is mathematically equivalent to (2) it follows that (1) equivalently expresses the foundation of Lagrangian mechanics
Is that where you disagree?
That is: do you submit that (1) and (2) are not mathematically interconvertable?
Equations can always be rearranged to accomodate specific circumstances. If circumstances are encountered where some derivative becomes problematic then you work around that with a suitable rearrangement.
So, sure, in the specific case that you describe the equation will have to be rearranged to accommodate the specifics of that case, such that the derivatives used are always defined.
The point is: we know that applying Lagrangian mechanics in multiple particle cases is a solved problem. On the grounds of that it is extremely implausible that the specific example that you discuss would constitute a problem to application of Lagrangian mechanics.