Post by: hamdani yusuf on 29/09/2021 04:53:12
Quote
For 50 years, mathematicians have believed that the total number of real numbers is unknowable. A new proof suggests otherwise.https://www.quantamagazine.org/how-many-numbers-exist-infinity-proof-moves-math-closer-to-an-answer-20210715/
There are an infinite number of infinities. Which one corresponds to the real numbers?
An Infinity of Infinities
Yes, infinity comes in many sizes. In 1873, the German mathematician Georg Cantor shook math to the core when he discovered that the “real” numbers that fill the number line — most with never-ending digits, like 3.14159… — outnumber “natural” numbers like 1, 2 and 3, even though there are infinitely many of both.
Infinite sets of numbers mess with our intuition about size, so as a warmup, compare the natural numbers {1, 2, 3, …} with the odd numbers {1, 3, 5, …}. You might think the first set is bigger, since only half its elements appear in the second set. Cantor realized, though, that the elements of the two sets can be put in a one-to-one correspondence. You can pair off the first elements of each set (1 and 1), then pair off their second elements (2 and 3), then their third (3 and 5), and so on forever, covering all elements of both sets. In this sense, the two infinite sets have the same size, or what Cantor called “cardinality.” He designated their size with the cardinal number0 (“aleph-zero”).
But Cantor discovered that natural numbers can’t be put into one-to-one correspondence with the continuum of real numbers. For instance, try to pair 1 with 1.00000… and 2 with 1.00001…, and you’ll have skipped over infinitely many real numbers (like 1.000000001…). You can’t possibly count them all; their cardinality is greater than that of the natural numbers.
(https://d2r55xnwy6nx47.cloudfront.net/uploads/2021/07/Infinity-graphic.svg)
Sizes of infinity don’t stop there. Cantor discovered that any infinite set’s power set — the set of all subsets of its elements — has larger cardinality than it does. Every power set itself has a power set, so that cardinal numbers form an infinitely tall tower of infinities.
Standing at the foot of this forbidding edifice, Cantor focused on the first couple of floors. He managed to prove that the set formed from different ways of ordering natural numbers (from smallest to largest, for example, or with all odd numbers first) has cardinality
His continuum hypothesis asserts that this is exactly the size of the continuum — that there are precisely
But to Cantor’s immense distress, he couldn’t prove it.
In 1900, the mathematician David Hilbert put the continuum hypothesis first on his famous list of 23 math problems to solve in the 20th century. Hilbert was enthralled by the nascent mathematics of infinity — “Cantor’s paradise,” as he called it — and the continuum hypothesis seemed like its lowest-hanging fruit.
To the contrary, shocking revelations last century turned Cantor’s question into a deep epistemological conundrum.
The trouble arose in 1931, when the Austrian-born logician Kurt Gödel discovered that any set of axioms that you might posit as a foundation for mathematics will inevitably be incomplete. There will always be questions that your list of ground rules can’t settle, true mathematical facts that they can’t prove.
As Gödel suspected right away, the continuum hypothesis is such a case: a problem that’s independent of the standard axioms of mathematics.
These axioms, 10 in all, are known as ZFC (for “Zermelo-Fraenkel axioms with the axiom of choice”), and they undergird almost all of modern math. The axioms describe basic properties of collections of objects, or sets. Since virtually everything mathematical can be built out of sets (the empty set {} denotes 0, for instance; {{}} denotes 1; {{},{{}}} denotes 2, and so on), the rules of sets suffice for constructing proofs throughout math.
In 1940, Gödel showed that you can’t use the ZFC axioms to disprove the continuum hypothesis. Then in 1963, the American mathematician Paul Cohen showed the opposite —you can’t use them to prove it, either. Cohen’s proof, together with Gödel’s, means the continuum hypothesis is independent of the ZFC axioms; they can have it either way.
What do you think about this continuum hypothesis?
Post by: hamdani yusuf on 29/09/2021 07:44:36
Quote
Not everything that is true can be proven. This discovery transformed infinity, changed the course of a world war and led to the modern computer.The video title sounds bombastic, perhaps deliberately to increase views.
IMO, the paradox and confusion comes from how we treat infinity.
Quote
https://brilliant.org/wiki/infinity/
Infinity is the concept of an object that is larger than any number. When used in the context "...infinitely small," it can also describe an object that is smaller than any number. It is important to take special note that infinity is not a number; rather, it exists only as an abstract concept. Attempting to treat infinity as a number, without special care, can lead to a number of paradoxes.
Infinity is not a number!
Quote
Because infinity is not a number, it requires special rules of arithmetic in order to remain consistent. This is a useful view in fields such as measure theory, which extends the real numbers by adding two numbers ∞ and −∞, that satisfy some additional rules:
a+∞ = ∞+a = ∞ (for any a besides −∞)
a−∞ = −∞+a = −∞ (for any a besides ∞)
a⋅∞ = ∞⋅a = −∞ (for positive a)
a⋅∞ = ∞⋅a = −∞ (for negative a)
a/∞ = a/-∞ = 0 (for real a)
∞/a = ∞ (for positive a)
∞/a = -∞ (for negative a)
It is worth noting that 1/0 is not ∞. Additionally, operations involving multiple infinities (such as ∞−∞ and ∞/∞) are not generally well-defined.
Importantly, note that this is an extension of the real numbers chosen specifically to allow infinity to be treated as a number; without this context, infinity remains a concept rather than a number. For instance, the following sections continue to treat infinity as a concept rather than a number, because the measure theory context above no longer applies
Post by: hamdani yusuf on 29/09/2021 07:57:20
IMO, the paradox and confusion comes from how we treat infinity.Here are some other rules commonly used for infinity, which are not included in previous post:
1/0 is not ∞ because the sign can't be defined.
∞.∞ = ∞
∞.-∞ = -∞
∞a = ∞ (for real a>0)
∞∞ = ∞
Post by: Eternal Student on 29/09/2021 09:25:18
I'm not sure what the question is.
How Many Numbers Exist? Many, much as described in the article. Unless you want to get philosophical and argue that numbers do not exist at all, they are just abstract.
What do you think about this continuum hypothesis? It can be an axiom in set theory but it doesn't have to be. It is independant of the ZF(C) axiom system (that's the Zermelo-Fraenkel axioms of set theory with or without the axiom of Choice). These are the axiom systems most commonly used. This just means that you can include the continuum hypothesis as an axiom if you want to, it doesn't invalidate the rest of the axioms. It's also not required for most things, for example you can still construct the Real Numbers without it, it's just that you wouldn't know if there was a set with cardinality between ℵ and ℜ. This wouldn't matter as far as, say for example Applied Mathematicians are concerned, you could still construct tools like calculus with the axioms in ZFC and do everything else that you might want to do.
If you want a more general discussion: The rules of arithmetic you are presenting in the later posts are for an object called the Extended Real Numbers. This is just a partial extension of the field of Real numbers, in particular it isn't a field. Not all of the field operations are defined for this ∞. For example 0 x ∞ is undefined.
From the point of view of the Pure mathematician's, this makes it fairly uninteresting and it does nothing more than act as shortcut for Applied Mathematicians rather than calculating limits more formally.
A more interesting object is the Hyperreal Numbers which is a proper field extension of the Reals.
There is a uniqueness theorem for the Real Numbers that holds in the ZFC axiom system. It states that the Real Numbers are the the only complete, ordered and Archimdean field. This means that a proper field extension has to lose at least one of those properties. The Hyperreal Numbers, for example, are totally ordered but they are not Archimedean. It doesn't matter too much, they are loads more fun anyway.
Best Wishes.
Post by: hamdani yusuf on 29/09/2021 13:31:28
Infinity Paradoxes - Numberphile
Quote
Infinity can throw up some interesting paradoxes, from filling Hilbert's Hotel to painting Gabriel's Trumpet... Mark Jago is a philosophy lecturer with a background in computer science.
The following videos are from Zach Star.
Things get weird at infinity
What happens at infinity? - The Cantor set
Post by: Eternal Student on 29/09/2021 17:35:56
Of the videos you've posted, which ones would you actually recommend and why?
There's 15 minutes x 3 videos = nearly an hour of stuff.
Best Wishes.
Post by: Zer0 on 29/09/2021 18:43:34
If i was " Eternal "...
Then i would simply just keep counting until Eternity.
To escape immortal boredom, i might count randomly..
Say 1,2,3,7,8,9,6,5,4...on n on so that none of the numbers were ever repeated.
Noone has ever reached the end point of Infinity, Right?
Just like giggles & laughter.
🤭
Ps - Say if i had the last laugh or the last word, n die abruptly, then did i really have the last laugh or the last word?
Pretty much seems like it, Who quarrels or debates with the dead anyway.
♾️
Post by: Eternal Student on 29/09/2021 23:06:00
Isn't " Infinity " Not a value, but just a never ending process.Yes, sometimes. Overall this would be a better way of thinking about it. Well done.
Best Wishes.
Post by: hamdani yusuf on 30/09/2021 02:43:07
Hi again.I recommend all of them, otherwise I wouldn't put them here in the first place.
Of the videos you've posted, which ones would you actually recommend and why?
There's 15 minutes x 3 videos = nearly an hour of stuff.
Best Wishes.
The last video is the continuation of the second, so it's not recommended to go straight to the last one.
Post by: hamdani yusuf on 30/09/2021 03:07:35
Moreover,
∞∞ = ∞
And we can stack those infinity power as many times as we want, and the answer is the same.
So, if we reject Cantor's method, the conundrum would disappear.
Post by: Eternal Student on 30/09/2021 11:42:36
I hope you are well and I'm delighted that someone has posted something about Mathematics.
I recommend all of them, otherwise I wouldn't put them here in the first place.OK. I'm not able to watch an hour of videos at the moment, sorry. Those videos don't have subtitles and when I can't see the presenter I have little idea what they are saying half the time so I can't engage with those videos very much.
The last video is the continuation of the second, so it's not recommended to go straight to the last one.
IMO, the continuum hypothesis conundrum occurs when we accept the validity of Cantor's method to define cardinality of number set.Cantor did lots of things. What are you calling "the Cantor method"?
Why is the Continuum hypothesis a conundrum?
....either the continuum hypothesis or its negation can be added as an axiom to ZFC set theory, with the resulting theory being consistent if and only if ZFC is consistent.... [From Wikipedia]
The continuum hypothesis is independent of the ZFC axiom system, you can accept or reject it or leave it indeterminable. It's interesting to Pure Mathematicians but it makes no difference to the majority of Mathematics that is in current use.
IMO, the continuum hypothesis conundrum occurs when we accept the validity of Cantor's method to define cardinality...........So, if we reject Cantor's method, the conundrum would disappear.The continuum hypothesis is the assumption that there isn't a set with cardinality between the set of Naturals (ℵ) and the set of the Real Numbers (ℜ).
If you don't have a definition of "cardinality" or decide to use a different one from every one else, then yes, the hypothesis changes it's meaning and/or becomes meaningless.
For example, we could define the cardinality of every infinite set to be C (whatever you want C to be, perhaps it's a symbol like ∞), then obviously every infinite set has cardinality C and so there isn't an infinite set with cardinality between ℵ and ℜ.
However, it should still make sense to talk about bijections and then the continuum hypothesis can be rephrased to restore it's original meaning: Is there a set S such that ℵ
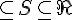but no bijections can be found from ℵ →S and S→ℜ.We consider bijections to be important because, IMO, that is how human beings compare things. We tend to put things into 1-to-1 correspondence with other things. This is how we can count a number of cows in a field, we find a correspondence between the first n counting numbers and the cows. We point to each cow but only once and don't stop until all cows have been pointed at. We're careful to start at the number 1 and increment by 1 each time, so we are establishing a bijection from {Cows} → {first n counting numbers}. We say that there are n cows but this is just shorthand for saying "I have found a bijection between the set of cows and the first n counting numbers". Bijections are the most natural way of comparing the size of two sets. We can compare the number of cows to a number of sheep in a different field.... we go and count the sheep by the same process.... establish a bijection from {Sheep} to the {first m counting numbers}. Now if m = n then we can combine the two bijections
{Cows} → {first n counting numbers} => {first m counting numbers} → {Sheep}
The bijection labeled => from {first n counting numbers} to {first m counting numbers} exists provided m=n, the identity mapping will do, i.e. the two sets are identical anyway. We obtain an overall bijection from {Cows} → {Sheep}. We say there are the same number of cows and sheep but this is just shorthand for saying "there is a bijection between the set of cows and the set of sheep". If m≠n then no bijection between the {cows} and {sheep} can be found.
Anyway.... spend a moment and think about what you've actually always been doing when you count things, you've always been finding bijections. The definition of "cardinality" where two sets have the same cardinality if and only if there exists a bijection between them wasn't arbitrarily decided upon. It is one of the most natural ways to compare the size of two sets.
Best Wishes.
Post by: hamdani yusuf on 30/09/2021 14:42:06
OK. I'm not able to watch an hour of videos at the moment, sorry. Those videos don't have subtitles and when I can't see the presenter I have little idea what they are saying half the time so I can't engage with those videos very much.I've added the titles of each videos to help referring which is which in discussion.
Post by: hamdani yusuf on 30/09/2021 14:43:19
Cantor did lots of things. What are you calling "the Cantor method"?You can read in the opening post.
Why is the Continuum hypothesis a conundrum?Please read again the opening post.
To the contrary, shocking revelations last century turned Cantor’s question into a deep epistemological conundrum.
Post by: Eternal Student on 30/09/2021 16:06:15
Quote
ES: What are you calling "the Cantor method"?Can't find "Cantor method" as a phrase in the OP.
HY: You can read in the opening post.
Best guess ---> it's the idea of finding bijections between sets.
To the contrary, shocking revelations last century turned Cantor’s question into a deep epistemological conundrum.I can't find "Cantor's question" in the article except in this one sentence.
Best Guess ----> the question was supposed to be "is the continuum hypothesis provable?"
If you were just after an answer to that ---> "No it can't be proved in the ZFC axiom system but neither can it be falsified in the ZFC system".
It's also a PopSci article, they say it's "a deep epistemological conundrum" - but they are not likely to say anyting else.
Going back to your earlier statement:
if we reject Cantor's method = ?? bijections to define cardinality ??This was discussed below. You're absolutely right, we could just define the size or cardinality of all infinte sets to be ∞. It's a definition of cardinality that is of limited use but it does show that infinite sets are bigger than finite sets, which is enough information in many situations.
, the conundrum would disappear.
Best Wishes.
Post by: hamdani yusuf on 01/10/2021 05:25:44
Can't find "Cantor method" as a phrase in the OP.You guess it right. In the article, it's shown in picture format.
Best guess ---> it's the idea of finding bijections between sets.
I can't find "Cantor's question" in the article except in this one sentence.From the article,
Best Guess ----> the question was supposed to be "is the continuum hypothesis provable?"
Quote
But to Cantor’s immense distress, he couldn’t prove it.
Post by: Eternal Student on 01/10/2021 13:42:49
Like the many short articles for the general public, they miss out several fine details.
Here's one example:
Suppose you had an enumeration of the real numbers that looked like this:
1 → 0.099999....... (recurring digit 9)
2 → 0.19378652...
3 → 0.4793656.....
4 → 0.39592478...
............
The first number has recurring digit 9, it is 0.0999999...
The next numbers in the enumeration need to have the digit 9 in the nth decimal place BUT all other digits are arbitrary.
Now build your test number as directed in the article (add 1 to the digit and note that 9 gets taken to 0), I've made the appropriate diagonal digits glow,
Our test number = 0.1000000.... = 0.1
However, you might have seen the mathematical result that shows
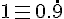
So that our test number, 0.1 is precisely equivalent to 0.0999999999..... which was the first number in the enumeration. So in this enumeration, the construction has failed to produce a number that wasn't on the list. We would be unable to conclude that this enumeration wasn't a total enumeration of the real numbers.
The requirement that there is a 9 in the (n)th decimal place isn't as restrictive as you might think. We could still argue that all real numbers between 0 and 1 might lie in that enumeration. Consider, for example, the number 0.1239321. It might seem that it has only has one 9 digit in the 4th decimal place and so it would have to be the number 4th on our list but this isn't true. It's the same number as 0.123932099999999999999999.... (replace the last digit 1 with infinitely recurring 9) - so that it could be anywhere on the list from the 8th entry on the list through to the ∞ entry on the list.
There's several places where the article has rushed or glossed over some complications that arise but it does what it set out to do well enough. It's an interesting article that appeals to the general public, keeps them on the edge of their seat and more importantly makes the reader feel that they have understood something. We all tend to learn more and feel more motivated by successfully understanding something. It should help to get people interested in Mathematics, so thanks for presenting it here.
Best Wishes.
{Late editing: Fixed some mistakes over nth and (n+1) th decimal place.}
Post by: hamdani yusuf on 02/10/2021 06:58:57
This was discussed below. You're absolutely right, we could just define the size or cardinality of all infinte sets to be ∞. It's a definition of cardinality that is of limited use but it does show that infinite sets are bigger than finite sets, which is enough information in many situations.It's mind boggling that many brilliant mathematicians over a century failed to see this, while a few random forum members can solve it in just a few posts. Perhaps we can collaborate to write a proper research paper on this.
Post by: hamdani yusuf on 02/10/2021 14:01:54
Math Has a Fatal FlawInstead of blaming math, we should do introspection to check on the validity of our method/derivation involving infinity or zero. When used incorrectly, we would be able to "proof" that 1=2, like an example below.
IMO, the paradox and confusion comes from how we treat infinity.
Quote
How to "Prove" That 2 = 1
Let's begin our journey into the bizarre world of apparently correct, yet obviously absurd, mathematical proofs by convincing ourselves that 1 + 1 = 1. And therefore that 2 = 1. I know this sounds crazy, but if you follow the logic (and don't already know the trick), I think you'll find that the "proof" is pretty convincing.
Here's how it works:
Assume that we have two variables a and b, and that: a = b
Multiply both sides by a to get: a2 = ab
Subtract b2 from both sides to get: a2 - b2 = ab - b2
This is the tricky part: Factor the left side (using FOIL from algebra) to get (a + b)(a - b) and factor out b from the right side to get b(a - b). If you're not sure how FOIL or factoring works, don't worry—you can check that this all works by multiplying everything out to see that it matches. The end result is that our equation has become: (a + b)(a - b) = b(a - b)
Since (a - b) appears on both sides, we can cancel it to get: a + b = b
Since a = b (that's the assumption we started with), we can substitute b in for a to get: b + b = b
Combining the two terms on the left gives us: 2b = b
Since b appears on both sides, we can divide through by b to get: 2 = 1
Wait, what?! Everything we did there looked totally reasonable. How in the world did we end up proving that 2 = 1?
https://www.quickanddirtytips.com/education/math/how-to-prove-that-1-2
Post by: Eternal Student on 02/10/2021 17:30:32
Instead of blaming math,....I'm lost. Who was blaming Maths? Only the person who wrote the original article in the first post, or was it someone else? I'll bet it was Alancalverd, it's always him.
Math Has a Fatal FlawIt's incomplete where the phrase is used in the sense of formal Mathematical logic and axiom systems. It's interesting but it's not fatal.
I don't think Mathematics has enough general interest so words like "fatal flaw" and "free food" are sometimes used when promoting lectures to the general public.
Best Wishes.
Post by: hamdani yusuf on 02/10/2021 18:18:40
I'm lost. Who was blaming Maths? Only the person who wrote the original article in the first post, or was it someone else? I'll bet it was Alancalverd, it's always him.It's from the title of Veritasium's video, which I quoted. You can click on the hyperlink to go to my post containing the video.
Post by: hamdani yusuf on 02/10/2021 18:33:14
Quote
In mathematics, the Riemann sphere, named after Bernhard Riemann,[1] is a model of the extended complex plane, the complex plane plus a point at infinity. This extended plane represents the extended complex numbers, that is, the complex numbers plus a value ∞ for infinity. With the Riemann model, the point "∞" is near to very large numbers, just as the point "0" is near to very small numbers.In Riemann sphere, there's oly one point of infinity. ∞=-∞=∞i=-∞i
(https://upload.wikimedia.org/wikipedia/commons/thumb/a/a1/RiemannKugel.svg/480px-RiemannKugel.svg.png)
The extended complex numbers are useful in complex analysis because they allow for division by zero in some circumstances, in a way that makes expressions such as 1/0=∞ well-behaved. For example, any rational function on the complex plane can be extended to a holomorphic function on the Riemann sphere, with the poles of the rational function mapping to infinity. More generally, any meromorphic function can be thought of as a holomorphic function whose codomain is the Riemann sphere.
But arithmetic operations involving multiple infinities can be messy.
Let's say ∞+∞=∞.
But ∞=-∞
Hence ∞+∞=∞-∞= undefined.
Post by: Eternal Student on 02/10/2021 21:52:50
It's mind boggling that many brilliant mathematicians over a century failed to see this, while a few random forum members can solve it in just a few posts. Perhaps we can collaborate to write a proper research paper on this.Since no other random forum members seem to be interested, I suppose I've got to ask. What did you have in mind? ...and is there any food or light refreshements provided because it might influence my decision.
Best Wishes.
Post by: hamdani yusuf on 03/10/2021 06:32:52
Since no other random forum members seem to be interested, I suppose I've got to ask. What did you have in mind? ...and is there any food or light refreshements provided because it might influence my decision.I see there are two other members involved in this thread. Their posts here show that they are interested to the topic.
I think that diagonal argument produces more problems and inconsistencies, rather than being useful to solve other problems. So, getting rid of it could help mathematics to move forward and restore its consistency.
Quote
https://en.wikipedia.org/wiki/Cantor%27s_diagonal_argumentPragmatically, our work could save a lot of person hours of talented people from fruitlessly trying to solve problems created by flawed foundation. Hence they would be able to use their time and efforts for some other things that are more useful.
(https://upload.wikimedia.org/wikipedia/commons/b/b7/Diagonal_argument_01_svg.svg)
An illustration of Cantor's diagonal argument (in base 2) for the existence of uncountable sets. The sequence at the bottom cannot occur anywhere in the enumeration of sequences above.
In set theory, Cantor's diagonal argument, also called the diagonalisation argument, the diagonal slash argument, the anti-diagonal argument, the diagonal method, and Cantor's diagonalization proof, was published in 1891 by Georg Cantor as a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence with the infinite set of natural numbers.[1][2]: 20– [3] Such sets are now known as uncountable sets, and the size of infinite sets is now treated by the theory of cardinal numbers which Cantor began.
The diagonal argument was not Cantor's first proof of the uncountability of the real numbers, which appeared in 1874.[4][5] However, it demonstrates a general technique that has since been used in a wide range of proofs,[6] including the first of Gödel's incompleteness theorems[2] and Turing's answer to the Entscheidungsproblem. Diagonalization arguments are often also the source of contradictions like Russell's paradox[7][8] and Richard's paradox.[2]: 27
Post by: Eternal Student on 03/10/2021 12:19:37
You haven't really answered the first question:
Perhaps we can collaborate to write a proper research paper on this.Where and how did you propose it would be published? Although, I don't suppose that's important, you could call something a paper even if it wasn't published anywhere. The main thing is what do you want to produce and what do you think will happen to it?
- - - - - - - -
I'm asking because I'm always wondering what the users hope to get from using this website. It's set up to be a forum, which is very roughly a place where things can be discussed. I use it for that purpose.
You have a noble sentiment about saving other people time and effort, which is great. However, I don't see how this forum will achieve what you are hoping for. Most professionals will search through published journals and not forums to find a paper. This is why I'm focusing on the first question - how did you intend to get the paper published or made available to others?
Best Wishes.
Post by: hamdani yusuf on 03/10/2021 12:51:04
This is why I'm focusing on the first question - how did you intend to get the paper published or made available to others?When the paper is finished, perhaps we can just send it to ArXiv, or it's alternative like Vixra. Considering the widespread interest on this subject, I think once published, it will reach wider audience in no time.
Post by: Eternal Student on 03/10/2021 21:40:57
perhaps we can just send it to ArXiv, or it's alternative like Vixra. Considering the widespread interest on this subject, I think once published, it will reach wider audience in no time.Arxiv will not take articles that are submitted by unregistered authors UNLESS these articles are endorsed by others (who are already registered authors). It's not as simple as sending a copy to Arxiv by mail and expecting them to make it available to the world. The usual way to obtain endorsement is to be affiliated with a recognised University or research establishment. To the best of knowledge, the Naked Scientists forum is not one of those recognised establishments.
Vixra is an alternative but take some time to read what they say about themselves:
ViXra.org is an e-print archive set up as an alternative to the popular arXiv.org service..... It has been founded by scientists who find they are unable to submit their articles to arXiv.org because of Cornell University's policy of endorsements and moderation designed to filter out e-prints that they consider inappropriate....
ViXra is an open repository for new scientific articles. It does not endorse e-prints accepted on its website, neither does it review them against criteria such as correctness or author's credentials. - taken from Vixra website, foot note on their main page. (Active link omitted since I can't even recommend that you visit. No one is entirely sure who pays for or maintains this website).
It takes only a moment to realise that there are very few quality checks on anything published on Vixra. There are some people who have gone so far as to say the following:....
Warranted or not, it has a reputation of being an alternative to arXiv for cranks and to host a lot of junk science, fake proofs or even outright nonsense. It is not recommended to submit something to viXra if you wish to be taken seriously, because the reputation of viXra would probably taint your paper's reputation by association.
- Taken from Academia stackexchange website. https://academia.stackexchange.com/questions/105518/what-are-the-differences-between-vixra-org-and-arxiv-org
Even if you did get endorsement from someone and got a paper to Arxiv, this still doesn't count as any formal publication. The articles and papers on Arxiv are not peer-reviewed in the same way as more conventional papers published in journals. More importantly there are thousands of articles on Arxiv and even they (Arxiv) explain that there is no reason to expect anyone else to find or see your article. You have to actively go out and make contact with others working in the field and invite them to look at the article. Only after your article has been cited a few times does it stand any chance at all of being found by other academics or the sort of people who you are trying so hard to help.
Even after this, the only way to really get it into the mainstream of education and further research is to get it properly published and subjected to a peer-review process in some proper journal. Most professionals do not have the time to study new articles on Arxiv, they barely have enough time to review articles that do get published in journals.
I can only apologise for writing so much, it's just that publishing a research paper isn't a simple matter.
Considering the widespread interest on this subject, I think once published, it will reach wider audience in no time.There is no history that I am aware of where something like a New Theory article presented in a forum has become a shortcut to getting a proper research paper published. I doubt it will get published to begin with.
Forgetting about outside interest, the interest here in this forum doesn't seem to be as "widespread" as you might have hoped. I'm really sorry but maybe Maths isn't to most people's liking, or maybe there just isn't more than half-a-dozen people here in the forum on a typical day.
- - - - - -
Anyway, I've already written too much and it's getting boring, sorry. I'm just asking you to take a moment to evaluate the situation.
You said....
Perhaps we can collaborate to write a proper research paper on this.I'm guessing you were talking to me. Let's say yes, yes I would. How is it going to be possible?
I'll answer some of the other subject-related questions or ideas you had in another post, I've already gone on too long here. Using the forum to discuss things seems useful and if you have a genuine interest in this subject, great, let's discuss it.
Best Wishes.
Post by: hamdani yusuf on 04/10/2021 04:10:24
There is no history that I am aware of where something like a New Theory article presented in a forum has become a shortcut to getting a proper research paper published. I doubt it will get published to begin with.I take the discussion here as brainstorming process, which is to collect as many information as possible, and perform initial filter to remove erroneous and irrelevant data from further consideration. It's an early phase of writing a research paper instead of a shortcut. Historically, one of the most influential research paper, Newton's Principia, was published as a result of communication between Newton and Halley. The earlier process itself began when Newton visited an apple garden. Private correspondence between Pascal and Fermat, as well as between Darwin and Wallace, also initiated the publication of important research papers. I don't see any downside of starting the research paper from an open correspondence in a forum, except from someone else stealing the idea for themselves. But at least we would already have left our digital footprint to stake our claim of priority in case the idea is recognised as important in the future.
Forgetting about outside interest, the interest here in this forum doesn't seem to be as "widespread" as you might have hoped. I'm really sorry but maybe Maths isn't to most people's liking, or maybe there just isn't more than half-a-dozen people here in the forum on a typical day.
Quote
It is inevitable that viXra will therefore contain e-prints that many scientists will consider clearly wrong and unscientific. However, it will also be a repository for new ideas that the scientific establishment is not currently willing to consider. Other perfectly conventional e-prints will be found here simply because the authors were not able to find a suitable endorser for the arXiv or because they prefer a more open system. It is our belief that anybody who considers themselves to have done scientific work should have the right to place it in an archive in order to communicate the idea to a wide public. They should also be allowed to stake their claim of priority in case the idea is recognised as important in the future.
https://vixra.org/why
Post by: hamdani yusuf on 04/10/2021 05:44:46
Quote
Math can be shortI have a dream.
Math can be hard and tedious resulting in very long papers. The 1995 proof of Fermat's last Theorem was 108 pages long.
But math can also be short.
Lander and Parkin's paper about a conjecture by Euler (related to Fermat's last Theorem), is probably the dream of everyone ever written a paper: It answers an interesting and important question, it's correct beyond any doubt, it's easy to understand and only two sentences long.
(https://cdn.paperpile.com/blog/img/lander-1966-1200x675.png?v=53)
Perhaps our paper wouldn't be that short, but at least we can try to minimize unnecessary things there.
Post by: Eternal Student on 04/10/2021 15:30:38
Let's start with a much earlier comment where a proof that 1=2 was presented.
Instead of blaming math, we should do introspection to check on the validity of our method/derivation involving infinity or zero. When used incorrectly, we would be able to "proof" that 1=2, like an example below.The proof was trivially incorrect and probably doesn't need much discussion. There was a division by 0, which I expect you were already aware of.
There isn't much "introspection" required, division by 0 isn't supported in the algebraic structures that were being used and assumed in that proof.
It's from the title of Veritasium's video, which I quoted. You can click on the hyperlink to go to my post containing the video.I've had enough time to watch that Veritasium video. It's Pop Sci rather than a rigourous derivation of the Godel theorem and I'm afraid it does make at least one mistake.
When discussing the Godel incompleteness theorem there is no detail provided about the process of "proof" using a formal first order logic and the presenter simplifies the proof provided by Godel to the point where it became incorrect.
He mentioned a "card" that stated "there is no proof for the statement with godel number g" and then assumed that card woud have Godel number g. This is evidently an unreasonable assumption. The Godel number is determined by the process he described earlier, it is 2a . 3b. 5c . 7d....... = some product of primes determined by the symbols that appear on the card. Regrettably, having the number g in the statement on that card means that the number g must be treated as a symbol, so it contributes to the overall Godel number you would calculate for that card. So you would have to guess what the over-all Godel number would be before you calulate it because you have to know what number g you need to include in that statement. Assuming the number g is quite large it is written as ssss....ss0 (the g th successor of 0) and so it influences the overall Godel number by a factor of p1σp2σp3σ....pgσ where σ = the Godel code number assigned to the succesor, s, symbol and pi are successive primes. In the general case there would be no solutions to this, we multiply g (the overall Godel number of the card) by a new prime pg >> 2 each time we just try to increase g by 1. You might need to re-watch the video and take a moment to identify this yourself.
Anyway, Godel's original proof follows the spirit of the method presented in that video but the fine details are different and that's what makes it work. Godel's test card actually involved a statement more like "This statement has no proof" and the over-all Godel number, g, of that statement does NOT appear in the statement.
- - - - - - - -
Summary: The Veritasium video is of interest to the general public but it's not completely accurate. It is not a substitute for studying Set theory, first order Logic and the original work of Godel. I'm not aware of any quick guides to these subjects, sorry. We didn't have a "Set theory" course although I know that some Universities do. Many undergraduate courses will just study and develop bits of set theory as and when required while covering over topics.
I think most of the better resources are going to be old-fashioned books rather than anything online.
Anyway, I've probably already spent too long here and I need to go and do some work.
Best Wishes.
Post by: Eternal Student on 05/10/2021 04:02:28
I'll try and say a bit more about some of your other posts.
The post you made earlier about the Riemann sphere is interesting although it's only vaguely related to any ideas of cardinality. This post is already long enough so I'll just move to the next topic. (Obviously you can raise the issue again if you did want to talk about it).
- - - - - - - - - - -
I think that diagonal argument produces more problems and inconsistencies, rather than being useful to solve other problems. So, getting rid of it could help mathematics to move forward and restore its consistency.Firstly, there isn't much reason to believe that our current system of mathematics is inconsistent. The continuum hypothesis doesn't demonstrate any inconsistency. It does however, indicate some incompleteness.
About Cantor's diagonalisation method
The main issue is that the diagonal argument or procedure exists. Choosing to ignore it or not to use it, doesn't make it go away. It's a perfectly valid procedure following form the ZFC axiom system and therefore any consequences that follow from it are properties of the mathematical structures that are constructed from this axiom system. Any attempt to deny or forbid some consequences that follow from the diagonalisation method (e.g. to assume that there actually is a bijection from ℵ to ℜ) will put inconsistencies into the system not remove them.
The only useful way to "remove" the diagonal argument (and hence also any problems that follow from it) would be to suggest a modification to the fundamental axioms. This is quite a serious proposition, if you expect your new axiom system to be useful to Mathematicians and Scientists. The favoured system is ZF(C), it has been developed for good reasons and is believed to be logically consistent. It isn't expected to be complete (i.e. not all true statements can be proved from the axioms) but so far it's been found to be quite sufficient or complete enough for most purposes.
Anyway, let's start from the beginning. You can certainly modify the fundamental axioms of your system of Mathematics and thus prevent the diagonalisation method from being valid, this is quite a trivial procedure. Your axiom system doesn't even have to be based on set theory if you wish. However, the system of axioms you have may then be seriously incomplete (i.e. insufficient for the majority of Mathematics that we actually use and therefore of little interest or practical value) or, worst of all, they may be inconsistent
I'm assuming from the posts you've written so far, that your intention is to have a system of mathematics that is useful for the world in which we live. For example, there would be a structure that looked and behaved as we would expect the Real numbers to behave. With this assumption we're really only looking at minor adjustments (if any) to the axiom system we commonly use.
One contentious issue in the diagonalisation argument
It's worth taking a moment to consider if there is a flaw in the procedure, or just a minor issue where only a small adjustment of the axioms might become relevant. The main issue that looks contentious is where it is assumed to be possible to construct a number so that its decimal digits will be different to ALL of the enumeration's diagonal decimal digits simultaneously.
If we look carefully at the procedure, it is clear that for any finite number, N, of decimal places, we can construct a test number so that it's digits will differ from the diagonal digits of the first N elements in the list. We can do this for any finite number of digits, N, no matter how large. The contentious issue is whether we can really "speed this up" to make infinitely many selections instantly.
If we have the axiom of choice in our set theory, then we can and the procedure is valid.
A weaker form of the axiom of choice called "the axiom of countable choice" would also be sufficient and the procedure would still be valid.
If we are steadfast and don't admit any version of the axiom of choice into our set theory, so that we are working in the ZF axiom system only then we have to be more careful. It is still possible to establish the existence of a well defined "choice function" but let's leave such things to one side for a moment and try to investigate exactly what might happen if we just deliberately choose an axiom system where the assumption of being able to identify the infinite set of digits is simply not permitted.
I've not really spent the time to formally establish exactly what the axiom system might be - but it would be reasonable to assume that some simple results concerning the limits of a sequence of real numbers should hold. Why is this reasonable? --> If these properties don't hold then the axiom system has become so limited or restrictive that it will be of little value in Mathematics anyway.
In Cantor's diagonalisation method, instead of declaring the test number, T, to be an infinite decimal with carefully chosen digits, we can declare T to be the limit of a sequence of numbers that have only finite digits.
Let T =
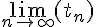
where each term of the sequence, tn, is determined to be the decimal with only n decimal places and given by the finite version of the usual selection rule. Specifically, the jth decimal digit of tn is one more than the jth decimal digit of the jth entry on the list (with digit 9 being mapped to 0).
It's only a small amount of work to verify that this limit has all the properties we would require (it would be a real number but it will be distinct from any number found on the list).
Summary In any reasonable axiom system, where the Real numbers would be complete* and finite selections can always be made, then the diagonalisation method (or the variant of it discussed above) will hold. This will establish that no bijection from ℵ to ℜ exists.
* Clarification on terminology: "Complete" in the sentence just above means that Cauchy sequences converge in ℜ. This is different to the term "complete" that is used when discussing Logic and axiom systems.
- - - - -
Now, it's possible to define the size or "cardinality" of sets in some way that doesn't involve finding bijections but this is just changing terminology and not changing the intrinsic properties of the structure. We can call a tiger by some other name but it will still act like a tiger. Someone will reasonably want to know if bijections exist between infinite sets (for reasons discussed in an earlier post). Similarly the diagonalisation method should hold in many other situations and not just for considering bijections from ℵ to ℜ. (NOTE: I haven't looked at every instance where something like this diagonalisation method is used, there are bound to be some applications that I am unaware of).
- - - - - - -
Obviously that's a long post, sorry and I should just stop for now. It's late and there's bound to be spelling and grammatical errors, sorry.
Best Wishes.
Post by: hamdani yusuf on 05/10/2021 23:56:00
The main issue is that the diagonal argument or procedure exists. Choosing to ignore it or not to use it, doesn't make it go away. It's a perfectly valid procedure following form the ZFC axiom system and therefore any consequences that follow from it are properties of the mathematical structures that are constructed from this axiom system.Many arithmetic procedures break down when infinity is involved. Otherwise we would prove that 1=2. I see no reason why diagonal procedure is somehow different.
I think it's easier and simpler to analyze it in binary form, since we only need to consider two possible values in each digit. If every possible combination of 0 and 1 is already covered in a set, then asserting that there are other sets containing other combinations not found in the first set is absurd. Hence it should not be used in further analysis.
Post by: Eternal Student on 06/10/2021 02:27:28
Many arithmetic procedures break down when infinity is involved. Otherwise we would prove that 1=2.Agreed.
I think it's easier and simpler to analyze it in binary form, since we only need to consider two possible values in each digit.O.K.
If every possible combination of 0 and 1 is already covered in a set, then asserting that there are other sets containing other combinations not found in the first set is absurd.Agreed. If it is true that the original set did cover all possible combinations of 0 and 1, then there can't be any other set containing other combinations not found in the first set.
However, the diagonalisation argument is used in a proof by contradiction. We aren't arbitrarily "asserting" that there other sets containing other combinations, we prove that there would be AND we don't really believe that the original set did cover all combinations of 0 and 1. We are just temporarily assuming that the original set covered all possibilities just to get set-up for a proof by contradiction. After this we will KNOW that the initial assumption we made had to be false. So the original set didn't really cover all possible combinations of 0 and 1.
Example
One of the easiest examples of a proof by contradiction is the proof that √2 is irrational, this is often seen at school.
Here's one website that presents the proof - https://www.mathsisfun.com/numbers/euclid-square-root-2-irrational.html
The typical use of the diagonalisation method is in a proof by contradiction. For example, this is how it is used to show that there isn't a bijection between ℵ and the interval [0,1] : Temporarily assume we have a bijection
F: ℵ → [0,1]. Then construct a test number, T, so that ........etc....... Ultimately we have T ∈ [0,1] but T ∉ Range(F). So F was NOT a bijection.
This is a contradiction, so our initial (temporary) assumption had to be false. Now we KNOW that there can't be a bijection from ℵ to the interval [0,1].
- - - - - - - - -
Sometimes it's best to say things in two different ways. Here's another approach:
If every possible combination of 0 and 1 is already covered in a set, then asserting that there are other sets containing other combinations not found in the first set is absurd.Agreed. The diagonalisation method can't be used to show the first set didn't cover all combinations of 0 and 1. If you define the set to be all possible combinations, then that is what it is. The diagonalisation method would only force the conclusion that this set cannot be "enumerated". It cannot be put into a 1-to-1 correspondence with the Natural numbers.
Best Wishes.
(Late editing - to try and keep mathematical expressions together on one line and not split over two lines)
Post by: hamdani yusuf on 06/10/2021 09:11:59
However, the diagonalisation argument is used in a proof by contradiction. We aren't arbitrarily "asserting" that there other sets containing other combinations, we prove that there would be AND we don't really believe that the original set did cover all combinations of 0 and 1. We are just temporarily assuming that the original set covered all possibilities just to get set-up for a proof by contradiction. After this we will KNOW that the initial assumption we made had to be false. So the original set didn't really cover all possible combinations of 0 and 1.My point was, I accept the validity of diagonalisation as long as it doesn't involve infinity.
Post by: Eternal Student on 06/10/2021 13:00:59
My point was, I accept the validity of diagonalisation as long as it doesn't involve infinity.I'm not sure what you meant by this.
It applies to sets that are either finite or else are not finite but can be enumerated (put into 1-to-1 correspondence with the natural numbers). When I say a set is finite or that it has finite size, we mean that it has a finite number of elements. To be very specific we have the following:
A set S is of finite size if and only if
There exists N∈ℵ and a bijection F: S → {1,2,3,....., N}
(and we would also allow S to be the empty set and say it has 0 size).
Sets of finite size are quite easy to work with. The only alternative is that a set is NOT of finite size and then, by definition, it is of infinite size. The diagonal argument does work with some infinite sets, it works with infinite sets that can be enumerated.
I think we need to discuss some basic history here. The Natural numbers are just the counting numbers 1,2,3,..... etc. People understood these. So defining and understanding the size of a set wasn't difficult when you can just count the elements in the set. The mathematical definition I gave above looks complicated but it isn't. It's just trying to set out formally what we mean when we say a set has N elements in it. It means we can find a bijection between the elements of the set and the first N counting numbers. So it turns out that "a set is of finite size" if and only if you can identify some Natural number, N and there is a bijection between the set and the first N counting numbers.
People wanted to extend this idea, finite sets can be bijectively mapped to a subset of the Naturals which is just the first N of these Natural numbers. So it was perfectly sensible to think that if you couldn't really map the elements of the set to the first N Natural numbers (no matter how large N might be) then it would still be possible to map the elements of the set to the entire set of Natural numbers. This is just saying - can we extend the idea of counting so that it never ends and we are in some sense counting all the way up to infinity? The early Mathematicians (before Cantor) thought that you could always do this. They believed that there was only one type of infinity, or that it would always be possible to "count" all the elements of a set, even if the set was of infinite size.
They were wrong. However, you need to be very precise about what you even meant by "counting" and "counting to infinity". These are just words, especially "counting to infinity" since this is not something you can actually do in reality. I've mentioned in earlier posts that we realised that our instinctive notions of counting things are actually all about finding bijections.
Anyway, Cantor didn't work with loosely defined phrases from the English language. He didn't consider some whimsical definition of "counting" or "counting to infinity". English language is no use in mathematics, it's subject to far too many personal interpretations. If you're a philosopher then you can still argue that all infinite sets are countable. However, mathematicians need a precise definition of the things they are working with. Cantor recognised that "counting" was about finding bijections with subsets of the Natural numbers. He effectively created the modern definition of what it means for an infinite set to be "countable".
It turns out that our best definition of what it means to count all the way to infinity is that we can find a bijection from the set of all Natural numbers to the set of things we were trying to count. Well, even if you don't agree that this is our "best definition" of counting all the way up to infinity, it is the one that is used. It is the formalisation of an intuitive way to count all the way to infinity as some extension of counting a finite number of things.
- - - - - - - - -
So that's the history over. Now we have the formal definition of a set having a finite size. The alternative is that the set is not finite and then we say it is of infinite size or that it has an infinite set of elements. The Natural numbers, for example, is not a finite set. Given any Natural number, N, we can obviously find more than N elements in the set of Natural numbers. The subset { 1, 2, 3, 4, ......, N, N+1 } is contained in the Naturals and it has size N+1 which is clearly greater than N. So the Natural numbers cannot have a finite size.
However the Natural numbers are the obvious example of a set that is infinite but can be enumerated. We can put the set of Naturals into a 1-to1 correspondence with the set of Naturals ---> The identify mapping will do it (just map 1 → 1; 2 → 2 and 3 → 3 ..... etc....... ).
So the diagonalisation argument does apply to one category of infinite sets. It applies to sets that aren't of finite size but can be enumerated. Rather than saying an infinite set can be enumerated, it is more common just to say that the set is countably infinite. A set is said to be countable if it is finite or countably infinite.
So if we take the example of the set of Natural Numbers, ℵ, this is infinite but it is countably infinite. Meanwhile the Real Numbers, ℜ, are also infinite but they are Uncountably infinite.
My point was, I accept the validity of diagonalisation as long as it doesn't involve infinity.The diagonalisation argument was developed specifically to analyse and characterise some infinite sets. It obviously involves infinity. It's useful for separating infinite sets into two types: Countably infinite sets and Uncountably infinite sets.
Best Wishes.
Post by: hamdani yusuf on 06/10/2021 15:16:18
But Cantor discovered that natural numbers can’t be put into one-to-one correspondence with the continuum of real numbers. For instance, try to pair 1 with 1.00000… and 2 with 1.00001…, and you’ll have skipped over infinitely many real numbers (like 1.000000001…). You can’t possibly count them all; their cardinality is greater than that of the natural numbers.Let's say that there's infinitely many real number between two consecutive natural numbers. Then there would be infinity times infinity many real number between 0 and infinity. But infinity squared is infinity.
Post by: hamdani yusuf on 06/10/2021 15:21:52
The diagonalisation argument was developed specifically to analyse and characterise some infinite sets. It obviously involves infinity. It's useful for separating infinite sets into two types: Countably infinite sets and Uncountably infinite sets.That's where the problem arises.
Sizes of infinity don’t stop there. Cantor discovered that any infinite set’s power set — the set of all subsets of its elements — has larger cardinality than it does. Every power set itself has a power set, so that cardinal numbers form an infinitely tall tower of infinities.
Standing at the foot of this forbidding edifice, Cantor focused on the first couple of floors. He managed to prove that the set formed from different ways of ordering natural numbers (from smallest to largest, for example, or with all odd numbers first) has cardinality 1, one level up from the natural numbers. Moreover, each of these “order types” encodes a real number.
His continuum hypothesis asserts that this is exactly the size of the continuum — that there are precisely 1 real numbers. In other words, the cardinality of the continuum immediately follow 0, the cardinality of the natural numbers, with no sizes of infinity in between.
But to Cantor’s immense distress, he couldn’t prove it.
Post by: Eternal Student on 06/10/2021 16:59:41
That's where the problem arises.You can't make these problems go away. In a sensible set theory like ZFC, you can construct Power sets, it's a perfectly well defined object and then these power sets will have a cardinality that exceeds the original set.
You highlighted a section :
But to Cantor’s immense distress, he couldn’t prove it.Which does NOT mean that it isn't true, neither does it mean that it is true. It just means Cantor couldn't prove it. In fact we now know that it's truth is independent of the ZFC axiom system, so it wasn't Cantor's fault in any way. He had no chance of proving or disproving it from the ZFC axioms.
You can add the continuum hyothesis into your set of axioms if you want to, or you can add the converse of the continuum hypothesis. Either of those extra axioms wouldn't create any inconsistency.
Let's say that there's infinitely many real number between two consecutive natural numbers. Then there would be infinity times infinity many real number between 0 and infinity. But infinity squared is infinity.This is a naive understanding of what infinity is. However, I'll go along with it. Where were you going with this? What was the problem? There's infinitely many real numbers between 0 and infinity...... and what's the problem with that?
Best Wishes.
Post by: hamdani yusuf on 07/10/2021 02:22:34
You can't make these problems go away. In a sensible set theory like ZFC, you can construct Power sets, it's a perfectly well defined object and then these power sets will have a cardinality that exceeds the original set.
I've posted a similar problem before.
How to "Prove" That 2 = 1Here is another excerpt from the same article continuing the quote above.
Let's begin our journey into the bizarre world of apparently correct, yet obviously absurd, mathematical proofs by convincing ourselves that 1 + 1 = 1. And therefore that 2 = 1. I know this sounds crazy, but if you follow the logic (and don't already know the trick), I think you'll find that the "proof" is pretty convincing.
Here's how it works:
Assume that we have two variables a and b, and that: a = b
Multiply both sides by a to get: a2 = ab
Subtract b2 from both sides to get: a2 - b2 = ab - b2
This is the tricky part: Factor the left side (using FOIL from algebra) to get (a + b)(a - b) and factor out b from the right side to get b(a - b). If you're not sure how FOIL or factoring works, don't worry—you can check that this all works by multiplying everything out to see that it matches. The end result is that our equation has become: (a + b)(a - b) = b(a - b)
Since (a - b) appears on both sides, we can cancel it to get: a + b = b
Since a = b (that's the assumption we started with), we can substitute b in for a to get: b + b = b
Combining the two terms on the left gives us: 2b = b
Since b appears on both sides, we can divide through by b to get: 2 = 1
Wait, what?! Everything we did there looked totally reasonable. How in the world did we end up proving that 2 = 1?
https://www.quickanddirtytips.com/education/math/how-to-prove-that-1-2
Quote
What Are Mathematical Fallacies?
The truth is we didn't actually prove that 2 = 1. Which, good news, means you can relax—we haven't shattered all that you know and love about math. Somewhere buried in that "proof" is a mistake. Actually, "mistake" isn't the right word because it wasn't an error in how we did the arithmetic manipulations, it was a much more subtle kind of whoopsie-daisy known as a "mathematical fallacy."
It's never OK to divide by zero!
What was the fallacy in the famous faux proof we looked at? Like many other mathematical fallacies, our proof relies upon the subtle trick of dividing by zero. And I say subtle because this proof is structured in such a way that you might never even notice that division by zero is happening. Where does it occur? Take a minute and see if you can figure it out…
OK, got it?
It happened when we divided both sides by a - b in the fifth step. But, you say, that's not dividing by zero—it's dividing by a - b. That's true, but we started with the assumption that a is equal to b, which means that a - b is the same thing as zero! And while it's perfectly fine to divide both sides of an equation by the same expression, it's not fine to do that if the expression is zero. Because, as we've been taught forever, it's never OK to divide by zero!
Why Can't You Divide By Zero?
Which might get you wondering: Why exactly is it that we can't divide by zero? We've all been warned about such things since we were little lads and ladies, but have you ever stopped to think about why division by zero is such an offensive thing to do? There are many ways to think about this. We'll talk about two reasons today.
The first has to do with how division is related to multiplication. Let's imagine for a second that division by zero is fine and dandy. In that case, a problem like 10 / 0 would have some value, which we'll call x. We don't know what it is, but we'll just assume that x is some number. So 10 / 0 = x. We can also look at this division problem as a multiplication problem asking what number, x, do we have to multiply by 0 to get 10? Of course, there's no answer to this question since every number multiplied by zero is zero. Which means the operation of dividing by zero is what's dubbed "undefined."
Post by: hamdani yusuf on 07/10/2021 02:24:07
This is a naive understanding of what infinity is.What is the non-naive understanding of infinity?
Post by: Eternal Student on 07/10/2021 13:41:48
I'm not sure what the relevance of the last posts were. I'm not sure what you were trying to say with it. I also don't think it would be helpful if I just repeat some of what I've said before.
Perhaps it would just be better to explain what it is you were or are hoping to do now or where you think there is a problem now.
Best Wishes.
Post by: Bored chemist on 07/10/2021 19:46:43
Assume that we have two variables a and b, and that: a = bAs you say,
Multiply both sides by a to get: a2 = ab
Subtract b2 from both sides to get: a2 - b2 = ab - b2
This is the tricky part: Factor the left side (using FOIL from algebra) to get (a + b)(a - b) and factor out b from the right side to get b(a - b). If you're not sure how FOIL or factoring works, don't worry—you can check that this all works by multiplying everything out to see that it matches. The end result is that our equation has become: (a + b)(a - b) = b(a - b)
Since (a - b) appears on both sides, we can cancel it to get: a + b = b
what you call "cancelling" is actually dividing each side by a-b
However, you start by saying that a = b
so a-b is zero.
so, that "cancelling" step is actually division by zero; it is forbidden.
More importantly, there are only 60 numbers- you can verify this by looking at a railway timetable.
Post by: hamdani yusuf on 08/10/2021 01:25:22
I'm not sure what the relevance of the last posts were. I'm not sure what you were trying to say with it.I was thinking that the problem introduced by the article in the op can't just go away because it contains a mathematical fallacy, like what I quoted in my latter post.
Post by: Eternal Student on 08/10/2021 02:19:20
I was thinking that the problem introduced by the article in the op can't just go away because it contains a mathematical fallacy, like what I quoted in my latter post.This sounds right.
The article isn't completely thorough about proving anything but the results they were talking about are widely recognised and there doesn't seem to be any mathematical fallacy in the more formal proofs of those results.
Best Wishes.
Post by: hamdani yusuf on 08/10/2021 06:38:54
The Natural numbers, for example, is not a finite set. Given any Natural number, N, we can obviously find more than N elements in the set of Natural numbers. The subset { 1, 2, 3, 4, ......, N, N+1 } is contained in the Naturals and it has size N+1 which is clearly greater than N. So the Natural numbers cannot have a finite size.Let's check if countability has a binary value. Assume that set of natural numbers is countable, while set of real numbers is uncountable. Then find a set more diluted than real numbers, and determine if it's still uncountable. Let's start with set of rational numbers. If you think it's countable, find another set that's denser. Otherwise, find another set that's more diluted. Repeat the process until threshold point is found.
However the Natural numbers are the obvious example of a set that is infinite but can be enumerated. We can put the set of Naturals into a 1-to1 correspondence with the set of Naturals ---> The identify mapping will do it (just map 1 → 1; 2 → 2 and 3 → 3 ..... etc....... ).
Post by: Eternal Student on 08/10/2021 11:31:32
Let's check if countability has a binary value.Not a phrase that is commonly used, so I can only guess what was wanted by reading the rest of the post.
Assume that set of natural numbers is countable, while set of real numbers is uncountable.OK. This is correct anyway.
Then find a set more diluted than real numbers, and determine if it's still countable.Dilution is another phrase that isn't commonly used. I'm going to assume that "dilution" means finding a subset.
Let's start with set of rational numbers.This is countable. This proof isn't too difficult. There are many methods to available for this. One easy approach is to note that any rational can be written as a/b where a and b are co-prime, this just means write the fraction in it's simplest form. Then map a/b to the integer 2a.3b. By the fundamental theorem of arithmetic, this identifies a unique integer to each rational.
There are some alternative proofs to be found here: https://proofwiki.org/wiki/Rational_Numbers_are_Countably_Infinite
If you think it's countable, find another set that's denser. Otherwise, find another set that's more diluted. Repeat the process until threshold point is found.Warning: The phrase "dense" isn't used in the way you're trying to use it here.
A set, S, is said to be "dense" in the Reals if and only if
For any real number r, we can always find a sequence of terms in S that converge to r <=>
∀r∈ℜ and ∀ε>0 , ∃s∈S such that | s - r | < ε
So, for example, the Rationals are countable but they are dense in the Reals.
However it seems that you are asking a slightly different question: Can we find a subset
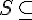ℜ such that every proper subset of S is countable but S is uncountable.The answer is no, you can't.
Proof: Assume (for contradiction) that we can find such a set S.
Then S is not empty because S is uncountable.
So there exists an element s∈S and then consider S \ {s} which is a proper subset of S.
Then S \ {s} is countable. Then S = S \ {s} U {s} is a countable union of countable sets.
So S is countable. →← (Contradiction obtained).
- - - - - - - - -
So there isn't any subset, S, of the Reals which would act as a "threshold", with all subsets of S being countable while all supersets of S are uncountable.
Best Wishes.
Post by: hamdani yusuf on 09/10/2021 10:41:05
Quote
https://en.wikipedia.org/wiki/Power_set#Properties
Cantor's diagonal argument shows that the power set of a set (whether infinite or not) always has strictly higher cardinality than the set itself (or informally, the power set must be larger than the original set). In particular, Cantor's theorem shows that the power set of a countably infinite set is uncountably infinite. The power set of the set of natural numbers can be put in a one-to-one correspondence with the set of real numbers (see Cardinality of the continuum).
Quote
https://en.wikipedia.org/wiki/Cardinality_of_the_continuumLet's assume that the power set of the set of natural numbers is uncountable. How do we determine the countability of less dense set of numbers, such as the power set of the set of prime numbers? or twin primes?
In set theory, the cardinality of the continuum is the cardinality or "size" of the set of real numbers R , sometimes called the continuum. It is an infinite cardinal number and is denoted by c (lowercase fraktur "c") or |R|.
The real numbers R are more numerous than the natural numbers N. Moreover, R has the same number of elements as the power set of N. Symbolically, if the cardinality of N is denoted as
(https://wikimedia.org/api/rest_v1/media/math/render/svg/d20f1f382986e00badaca55386d014b869c90b56)
This was proven by Georg Cantor in his uncountability proof of 1874, part of his groundbreaking study of different infinities. The inequality was later stated more simply in his diagonal argument in 1891. Cantor defined cardinality in terms of bijective functions: two sets have the same cardinality if, and only if, there exists a bijective function between them.
The smallest infinite cardinal number is
Post by: Eternal Student on 09/10/2021 22:19:54
Let's assume that the power set of the set of natural numbers is uncountable.Yes, good call.
How do we determine the countability of less dense set of numbers, such as the power set of the set of prime numbers? or twin primes?The set of primes is an infinite set. See Wikipedia for a proof and discussion: https://en.wikipedia.org/wiki/Euclid%27s_theorem
The set of all primes, P is obviously contained in the Natural numbers. So the identity mapping I: P →ℵ is an injective mapping. So we have |P| ≤ |ℵ| (where |S| denotes the cardinality of the set S. But P is inifnite so |P| ≥ |ℵ|. Hence, |P| = |ℵ| = ℵ0. This assumes results about the ordering of infinite cardinal numbers, which you can find discussed elsewhere (for example, https://en.wikipedia.org/wiki/Cardinal_number). As I recall we would require the axiom of choice to show that ℵ0 is the smallest infinite cardinal. If you're interested, we can check to see if this can be established without the axiom of choice and just in the ZF axiom system.
An alternative approach would be to use the fact that the primes are ordered, the order relation < defined on the Reals will be an order relation on the primes. So we should be able to order the primes from smallest to largest and then find a bijection from P → ℵ. (I haven't checked the results about well-ordered sets and I suspect we will still need the axiom of choice - but that's where I'd be looking first, if indeed you're worried about using the axiom of choice at all).
Anyway, the Power set of the primes must have a greater cardinality. If you wish to accept the continuum hypothesis, this would be the same as the cardinality of ℜ which, in turn, is the same as cardinality of the power set of Naturals. If you don't accept the continuum hypothesis then the Power set of the primes has a cardinality that can be written as 2|P|. I think we can still show that 2|P| = 2N0 if that's useful. It's just that, without the continuum hypothesis, we would know only that this is greater than ℵ0 but not necessarily equal to the cardinality of the continuum.
The twin primes are harder to work with, since we don't know if this is an infinite set. If it's a finite set, then finding the it's power set and the cardinality of it's power set is easy. If it's an infinite set then it has cardinality equal to that of Natural numbers (and for the same reasons as that shown above) and it's power set follows the same rules. I can tell you with certainty that the set of all twin primes is countable (it's either finite or countably infinite). However, we can't determine the cardinality of the Power set without knowing if the twin prime conjecture is true, i.e. if the set of all twin primes is infinite.
Minor note: Just because we can't (or I can't) identify the cardinality of the Power set of the twin primes, does not mean that it doesn't exist or that it will never be determined. It's just that I, personally, can't identify it.
If indeed the twin prime conjecture was ever proven, then the cardinality of the power set follows easily. Conversely, if the cardinality of the power set was known then the truth or falsehood of the twin prime conjecture follows easily. So, if the twin prime conjecture was shown to be undecideable (neither it's truth or falsehood can be established from the ZFC axioms) then the cardianlity of the power set of the set of twin primes remains undecideable.
Best Wishes.
Post by: Zer0 on 11/10/2021 09:32:53
😁
Dyscalculia!!!
But i still follow this OP.
Coz i Really Like what you both are doing in here.
👍
Different Individuals with different backgrounds & identities...moving forward towards a common goal.
👍
Not everybody can Collaborate soo Harmoniously.
Good Job!
Please keep up the Good Work.
🙏
Ps - There are Instances of " Aim & Hit & Miss "...But Real Failure is when One Stops Trying.
🖖
Post by: Eternal Student on 11/10/2021 23:15:38
SideNote - i am a self proclaimed & self diagnosed entity who has a self proclaimed Myself unfit for the Subject.(OP)Self-diagnosed? I don't know where you live but if it becomes useful or relevant you could get a formal test and diagnosis. It could be that something simple can be done. Maybe all you need are some coloured glasses and some classical music playing in the background, or less of something you're normally exposed to (like caffeine or some other substance).
Different Individuals with different backgrounds & identities...moving forward towards a common goal.Hopefully, that's what should be happening in most forum threads.
Anyway, I wish you well, Zer0. Bye for now.
Post by: BilboGrabbins on 12/10/2021 02:24:32
How Many Numbers Exist? Infinity Proof Moves Math Closer to an Answer.QuoteFor 50 years, mathematicians have believed that the total number of real numbers is unknowable. A new proof suggests otherwise.https://www.quantamagazine.org/how-many-numbers-exist-infinity-proof-moves-math-closer-to-an-answer-20210715/
There are an infinite number of infinities. Which one corresponds to the real numbers?
An Infinity of Infinities
Yes, infinity comes in many sizes. In 1873, the German mathematician Georg Cantor shook math to the core when he discovered that the “real” numbers that fill the number line — most with never-ending digits, like 3.14159… — outnumber “natural” numbers like 1, 2 and 3, even though there are infinitely many of both.
Infinite sets of numbers mess with our intuition about size, so as a warmup, compare the natural numbers {1, 2, 3, …} with the odd numbers {1, 3, 5, …}. You might think the first set is bigger, since only half its elements appear in the second set. Cantor realized, though, that the elements of the two sets can be put in a one-to-one correspondence. You can pair off the first elements of each set (1 and 1), then pair off their second elements (2 and 3), then their third (3 and 5), and so on forever, covering all elements of both sets. In this sense, the two infinite sets have the same size, or what Cantor called “cardinality.” He designated their size with the cardinal number
But Cantor discovered that natural numbers can’t be put into one-to-one correspondence with the continuum of real numbers. For instance, try to pair 1 with 1.00000… and 2 with 1.00001…, and you’ll have skipped over infinitely many real numbers (like 1.000000001…). You can’t possibly count them all; their cardinality is greater than that of the natural numbers.
(https://d2r55xnwy6nx47.cloudfront.net/uploads/2021/07/Infinity-graphic.svg)
Sizes of infinity don’t stop there. Cantor discovered that any infinite set’s power set — the set of all subsets of its elements — has larger cardinality than it does. Every power set itself has a power set, so that cardinal numbers form an infinitely tall tower of infinities.
Standing at the foot of this forbidding edifice, Cantor focused on the first couple of floors. He managed to prove that the set formed from different ways of ordering natural numbers (from smallest to largest, for example, or with all odd numbers first) has cardinality
His continuum hypothesis asserts that this is exactly the size of the continuum — that there are precisely
But to Cantor’s immense distress, he couldn’t prove it.
In 1900, the mathematician David Hilbert put the continuum hypothesis first on his famous list of 23 math problems to solve in the 20th century. Hilbert was enthralled by the nascent mathematics of infinity — “Cantor’s paradise,” as he called it — and the continuum hypothesis seemed like its lowest-hanging fruit.
To the contrary, shocking revelations last century turned Cantor’s question into a deep epistemological conundrum.
The trouble arose in 1931, when the Austrian-born logician Kurt Gödel discovered that any set of axioms that you might posit as a foundation for mathematics will inevitably be incomplete. There will always be questions that your list of ground rules can’t settle, true mathematical facts that they can’t prove.
As Gödel suspected right away, the continuum hypothesis is such a case: a problem that’s independent of the standard axioms of mathematics.
These axioms, 10 in all, are known as ZFC (for “Zermelo-Fraenkel axioms with the axiom of choice”), and they undergird almost all of modern math. The axioms describe basic properties of collections of objects, or sets. Since virtually everything mathematical can be built out of sets (the empty set {} denotes 0, for instance; {{}} denotes 1; {{},{{}}} denotes 2, and so on), the rules of sets suffice for constructing proofs throughout math.
In 1940, Gödel showed that you can’t use the ZFC axioms to disprove the continuum hypothesis. Then in 1963, the American mathematician Paul Cohen showed the opposite —you can’t use them to prove it, either. Cohen’s proof, together with Gödel’s, means the continuum hypothesis is independent of the ZFC axioms; they can have it either way.
What do you think about this continuum hypothesis?
Oh dear, the mathematicians in love with infinity pretending to be physicists. I'll put a damper on this quickly.
Infinity is a concept. If mathematicians claim infinity holds answers to calculable infinities, this had two massive errors. Not only is it a concept, it's not a number, its an array of numbers which are fundamentally uncountable. There are no infinities in nature.
Even if we made a machine that could count infinitely onwards, any observer going to the machine, at any point will never be infinite, no matter what number it will read on its screen. That means philosophically that infinity itself is not an observable and there is no finite machine capable of counting to infinity.
Infinity is a much abused concept and often while most physicists will agree with what I said, there's still a handful of physicists who hold onto it like it was the ring of Mordor.
Post by: BilboGrabbins on 12/10/2021 02:29:46
Post by: Bored chemist on 12/10/2021 13:40:43
There are no infinities in nature.There ae a infinite number of ways in which I can place a coffee table in a room.
Post by: Eternal Student on 12/10/2021 14:54:44
If mathematicians claim infinity holds answers to calculable infinities,These are words put together in a way that sounds poetical. I don't know what it means but it sounds cool.
That means philosophically that infinity itself is not an observable and there is no finite machine capable of counting to infinity.The last bit seems reasonable, there's no finite machine capable of counting to infinity. However, this means only that we can't count to infinity. Can you still observe an infinite set anyway? Well it probably depends on whether space and time is continuous or discrete. If, for example, there was something like a fundamental Planck length and the location of a particle can be only one of a finite set of choices then you might be right. Otherwise the sort of thing mentioned by @Bored chemist seems to apply.
In physics, we've been working meticulously to get rid of infinities from over a dozen crucial models, including those which we once thought existed inside of black holes or the beginning of the universe.You might be worrying yourself needlessly. I'm not sure if the OP (Hamdani) was really concerned about using infinity in some piece of Physics, you'd have to ask him. There isn't a Mathematics section in this forum. It seemed that the OP was asking something about Mathematics without any reference to some application in Physics.
Best Wishes.
Post by: BilboGrabbins on 12/10/2021 16:44:56
There are no infinities in nature.There ae a infinite number of ways in which I can place a coffee table in a room.
No you can't. Unless of course the room is infinite? But then how'd you know it's a room with walls?
And even if you could state that correctly, that would be a concept. You wouldn't be able to arrange a table an infinite amount of times. Such a concept is nonphysical. In fact infinities themselves are best defined in physics as unphysical concepts.
Post by: Eternal Student on 13/10/2021 13:02:42
Consider a race between the tortoise and the hare.
The hare travels at twice the speed of the tortoise. However, the hare allows the tortoise to get half-way along the race track before he starts.
They should both cross the finish line at the same time. Check this yourself.
Anyway, it is possible to consider how many times the distance between the hare and the tortoise has been halved.
They started with a distance D/2 between them when the hare began to run. (Where D = distance of the whole track).
When the hare was half way up the track.... the tortoise was only a quarter of the way from the finish.... the distance between them was then D/4
..... there was a time when they were D/8 apart.....
.... D/16 apart.... then D/32....... etc......
... we know that at the finish line they were 0 distance apart (they crossed the finish line together).
So the distance between them was halved "infinitely many" times.... and this all happened within a finite amount of time. The hare reached the finish line in an amount of time = D / (Speed of hare).
To phrase this another way: It seems perfectly realistic that you could have watched this race. It would only have taken a finite amount of time but during the race you would have seen the distance between the hare and tortoise being halved "infinitely many" times.
Best Wishes.
Post by: BilboGrabbins on 13/10/2021 18:40:57
I'm aware of this thought experiment... And no. You cannot divide infinitely. There is a physical stop sign in physics . Again, infinities are not physical things.
Post by: Bored chemist on 13/10/2021 19:08:11
No you can't. Unless of course the room is infinite? But then how'd you know it's a room with walls?Yes, I can.
I can align the table North/ South.
And there are an infinite number of angles through which I can then rotate it.
So that's an infinite number of "ways in which I can place a coffee table in a room."
Post by: BilboGrabbins on 13/10/2021 20:46:43
No you can't. Unless of course the room is infinite? But then how'd you know it's a room with walls?Yes, I can.
I can align the table North/ South.
And there are an infinite number of angles through which I can then rotate it.
So that's an infinite number of "ways in which I can place a coffee table in a room."
Lol. Are you being serious? A room has a finite boundary condition. You might get a hell of a lot of orientations but certainly not infinite. I don't like people misleading others into such baloney!
Post by: BilboGrabbins on 13/10/2021 20:48:58
Post by: Bored chemist on 13/10/2021 21:51:59
What boundary conditions stop me choosing an arbitrary angle?No you can't. Unless of course the room is infinite? But then how'd you know it's a room with walls?Yes, I can.
I can align the table North/ South.
And there are an infinite number of angles through which I can then rotate it.
So that's an infinite number of "ways in which I can place a coffee table in a room."
Lol. Are you being serious? A room has a finite boundary condition. You might get a hell of a lot of orientations but certainly not infinite. I don't like people misleading others into such baloney!
How many angles are there in the series 180, 90, 45, 22.5 ... and so on?
Which of them is forbidden?
Post by: Eternal Student on 13/10/2021 22:11:00
I'm aware of this thought experiment... And no. You cannot divide infinitely. There is a physical stop sign in physics .What physical stop sign in physics? Are you talking about an indivisible planck length? This was mentioned in reply #53. Otherwise lengths such as those in the tortoise and hare experiment or angles such as in Bored Chemist's example can be divided more times than any finite number of times (which is fair description of infintely many times) and it can often all be done within a finite amount of time.
Best Wishes.
Post by: BilboGrabbins on 13/10/2021 22:22:49
What boundary conditions stop me choosing an arbitrary angle?No you can't. Unless of course the room is infinite? But then how'd you know it's a room with walls?Yes, I can.
I can align the table North/ South.
And there are an infinite number of angles through which I can then rotate it.
So that's an infinite number of "ways in which I can place a coffee table in a room."
Lol. Are you being serious? A room has a finite boundary condition. You might get a hell of a lot of orientations but certainly not infinite. I don't like people misleading others into such baloney!
How many angles are there in the series 180, 90, 45, 22.5 ... and so on?
Which of them is forbidden?
First define how big the box is, and then you'll define the walls which would act as a boundary for all possible orientations. If we choose a simple room, which is the exact length of the table and one table stacked on the other defines the height, then how many orientations of a table can you make in this limited space?
Post by: BilboGrabbins on 13/10/2021 22:27:22
Hi again.I'm aware of this thought experiment... And no. You cannot divide infinitely. There is a physical stop sign in physics .What physical stop sign in physics? Are you talking about an indivisible planck length? This was mentioned in reply #53. Otherwise lengths such as those in the tortoise and hare experiment or angles such as in Bored Chemist's example can be divided more times than any finite number of times (which is fair description of infintely many times) and it can often all be done within a finite amount of time.
Best Wishes.
Yes the Planck length. This is the ground rule that prevents continuous divisibility.
Post by: Eternal Student on 13/10/2021 22:43:17
Yes the Planck length. This is the ground rule that prevents continuous divisibility.It's not a rule, it's one possibility. To the best of my knowledge we don't know that space is discrete rather than being continuous.
Best Wishes.
Post by: BilboGrabbins on 13/10/2021 22:48:21
Hi.Yes the Planck length. This is the ground rule that prevents continuous divisibility.It's not a rule, it's one possibility. To the best of my knowledge we don't know that space is discrete rather than being continuous.
Best Wishes.
It is a rule of physical length. No physicist doubts its existence. Well none I have spoken to.
Post by: BilboGrabbins on 13/10/2021 22:54:23
Post by: BilboGrabbins on 13/10/2021 22:59:56
Post by: BilboGrabbins on 13/10/2021 23:02:56
Post by: Eternal Student on 13/10/2021 23:32:19
It's fine for you to have your opinions. I have my opinions and in fact I'm in the middle ground: Space might be discrete or it might be continuous.
However, you need to be careful when you say something like this:
It is a rule of physical length. No physicist doubts its existence. Well none I have spoken to.It's not a universally accepted idea and you would need to cite some references.
Here's one reference that counters what you've said and there are many others.
..... space and time can be either continuous or discrete in a quantum Universe. But it means that if the Universe does have a fundamental length scale, that the CPT theorem, Lorentz invariance, and the principle of relativity must all be wrong. It could be so, but without the evidence to back it up, the idea of a fundamental length scale will remain speculative at best..... [Taken from "This is why space needs to be continuous", Forbes. https://www.forbes.com/sites/startswithabang/2020/04/17/this-is-why-space-needs-to-be-continuous-not-discrete/?sh=50c668d774ea ]
Best Wishes.
Post by: BilboGrabbins on 13/10/2021 23:48:39
Hi again.
It's fine for you to have your opinions. I have my opinions and in fact I'm in the middle ground: Space might be discrete or it might be continuous.
However, you need to be careful when you say something like this:It is a rule of physical length. No physicist doubts its existence. Well none I have spoken to.It's not a universally accepted idea and you would need to cite some references.
Here's one reference that counters what you've said and there are many others.
..... space and time can be either continuous or discrete in a quantum Universe. But it means that if the Universe does have a fundamental length scale, that the CPT theorem, Lorentz invariance, and the principle of relativity must all be wrong. It could be so, but without the evidence to back it up, the idea of a fundamental length scale will remain speculative at best..... [Taken from "This is why space needs to be continuous", Forbes. https://www.forbes.com/sites/startswithabang/2020/04/17/this-is-why-space-needs-to-be-continuous-not-discrete/?sh=50c668d774ea ]
Best Wishes.
I'm very up to date with these things. A more promising mathematical model has shown systems can be discrete and continuous at the same time.
Post by: BilboGrabbins on 14/10/2021 00:32:34
Post by: hamdani yusuf on 14/10/2021 07:49:27
Quote
You've all been indoctrinated into accepting that you cannot divide by zero. Find out about the beautiful mathematics that results when you do it anyway in calculus. Featuring some of the most notorious "forbidden" expressions like 0/0 and 1^∞ as well as Apple's Siri and Sir Isaac Newton.
In his book “Yearning for the impossible” one my favourite authors John Stillwell says “…mathematics is a story of close encounters with the impossible and all its great discoveries are close encounters with the impossible.” What we talk about in this video and quite a few other Mathologer videos are great examples of these sort of close encounters.
Post by: Bored chemist on 14/10/2021 08:43:45
If we choose a simple room, which is the exact length of the table and one table stacked on the other defines the height, then how many orientations of a table can you make in this limited space?No, lets not pick a stupid example, carefully chosen so that you seem to be right. It's particularly stupid choice given that I already specified an important parameter; I said I can rotate the table in the room. So the grownups know that your scenario is irrelevant.
Let's pick a real one. The coffee table in the room I'm in is about 1.5 m long and 0.7 m wide and the room is roughly square and about 4 metres on each side.
In reality there's an infinite number of possible angles I can align it on.
Post by: BilboGrabbins on 14/10/2021 11:19:54
If we choose a simple room, which is the exact length of the table and one table stacked on the other defines the height, then how many orientations of a table can you make in this limited space?No, lets not pick a stupid example, carefully chosen so that you seem to be right.
I beg your pardon? Chosing simple constructions in physics is actually EXACTLY how we should approach your stupid thought experiment.
Post by: Eternal Student on 14/10/2021 13:05:24
Indeterminate: the hidden power of 0 divided by 0 ......... (and video provided)...I can review the video, if that helps:
It was a 12 minute video. You can safely watch it in 6 minutes if you choose double-speed. Calculus was discussed and L'Hopitals rule. Something controversial was said about 5 seconds before the end, so you may like to slow it down for that. If you're new to calculus, this video might provide some useful graphics and explanation. If you're interested in L'Hopitals rule the video doesn't provide enough detail to help much.
Best Wishes.
Post by: hamdani yusuf on 14/10/2021 13:15:20
Quote
In today's video the Mathologer sets out to give an introduction to the notoriously hard topic of transcendental numbers that is both in depth and accessible to anybody with a bit of common sense. Find out how Georg Cantor's infinities can be used in a very simple and off the beaten track way to pinpoint a transcendental number and to show that it is really transcendental. Also find out why there are a lot more transcendental numbers than numbers that we usually think of as numbers, and this despite the fact that it is super tough to show the transcendence of any number of interest such as pi or e. Also featuring an animated introduction to countable and uncountable infinities, Joseph Liouville's ocean of zeros constant, and much more.
Post by: Eternal Student on 14/10/2021 14:08:57
I've got to ask: Do you know this Mathlogger person? Why are you promoting these videos? They're good - but what is this for? It takes time to watch these and you don't seem to want to discuss anything about them.
Best Wishes.
Post by: hamdani yusuf on 14/10/2021 14:31:41
Hi again.No. I posted here because they're related to the topic in this thread. They give us insight on how professional mathematicians are thinking about the problem. Or what they think is the best way to teach the problems to non-mathematicians.
I've got to ask: Do you know this Mathlogger person? Why are you promoting these videos? They're good - but what is this for? It takes time to watch these and you don't seem to want to discuss anything about them.
Best Wishes.
I have posted my criticism on Cantor's diagonal argument which is used in the videos. So I hope I'm not criticizing the wrong argument, which would make it a straw man fallacy.
Post by: Eternal Student on 14/10/2021 15:52:11
First of all I've just finished watching the second video about transcendetal numbers. That was 17 minutes long.
They give us insight on how professional mathematicians are thinking about the problem.Not really. There's nothing especially new that was presented in those videos. Most of this was known before 1900. Textbooks and lecture courses present the material in a way that is more useful to professional mathematicians. The videos, especially the Mathologger videos make it clear that they were trying to appeal to the general public and required only what he described as "common sense" to undertstand them.
...Or what they think is the best way to teach the problems to non-mathematicians.This is more likely. However, Mathologger wasn't really even trying to teach these topics in the usual sense of teaching. The videos were just about getting people interested and getting some views. They were what people describe as "edu-tainment" and not specifically as education. To phrase this another way, they were more for entertainment than anything else.
On the positive side, getting people interested is an important part of teaching and these videos would seem to be doing a good job of that.
I have posted my criticism on Cantor's diagonal argument which is used in the videos.Perhaps you should summarise your criticism on Cantor's diagonal argument again. I can only find references like this in thread:
I think that diagonal argument produces more problems and inconsistencies, rather than being useful to solve other problems. So, getting rid of it could help mathematics to move forward and restore its consistency.So, if I'm right then your criticism of the diagonal agrument is that it produces unusual consequences.
Sadly (actually it's not necessarily "sad", it's just really ineteresting), it does but "getting rid of it" isn't a realistic option. It's a valid procedure following from the axioms of the ZFC axiom systsem and so the consequences it reveals are properties that structures we construct from the ZFC axioms, like Real numbers and subsets of these, would have.
Do you think there is some fundamental flaw in Cantor's diagonalisation method? This would certainly be worth identifying.
OR ELSE, are you proposing that the ZFC axioms are not the most appropriate axiom system for the Real Numbers? I mean, you could well be right there, there is no universal agreement about what the fundamental axioms of Mathematics should be, it's just that ZF (with or without the Axiom of Choice) seems to work well.
Best Wishes.
Post by: Zer0 on 14/10/2021 18:47:21
Hi there!
🙋
I have a Query, Especially for You.
Interested?
A_______B
A simple line.
Start point A.
End point B.
I suppose i can keep dividing it into Halves.
But considering Planck's Length, Can i Divide it until Infinity?
If i Know the Line's point of Origin(A) & am Aware of the Line's point of Cessation(B)...Does that sound like Infinity?
Or if i didn't know the Origin, n was clueless bout the End.
Infinity!
Ps - Thanks E_S for the suggestions.
I've Realized my capacity to understand & learn is Not infinite.
Hence i do not bother myself, & also spare Others of goin thru the troubles of explaining me things which i Firmly Believe i shall never understand.
(Reason i Request for short & brief answers, i Hate it when Teachers waste their Precious Time on Futile Things)
: )
Post by: BilboGrabbins on 14/10/2021 19:08:11
@BilboGrabbins
Hi there!
🙋
I have a Query, Especially for You.
Interested?
A_______B
A simple line.
Start point A.
End point B.
I suppose i can keep dividing it into Halves.
But considering Planck's Length, Can i Divide it until Infinity?
If i Know the Line's point of Origin(A) & am Aware of the Line's point of Cessation(B)...Does that sound like Infinity?
Or if i didn't know the Origin, n was clueless bout the End.
Infinity!
Ps - Thanks E_S for the suggestions.
I've Realized my capacity to understand & learn is Not infinite.
Hence i do not bother myself, & also spare Others of goin thru the troubles of explaining me things which i Firmly Believe i shall never understand.
(Reason i Request for short & brief answers, i Hate it when Teachers waste their Precious Time on Futile Things)
: )
No, to divide through the Planck length infinitely many times would be equivelent to a singularity. That is itself equivelent to a breakdown in physics.
Post by: Eternal Student on 15/10/2021 15:30:05
I've Realized my capacity to understand & learn is Not infinite.Neither is mine. I was especially "thick" as a child and couldn't read, write or do arithmetic until I was about 10 years old. Fortunately the UK doesn't hold people back a year when they don't pass exams, so I did get out of primary school.
No, to divide through the Planck length infinitely many times would be equivalent to a singularity. That is itself equivelent to a breakdown in physics.This is about the limitations of our ability to probe below the planck length not the actual nature of space.
...The Planck length is expected to be the shortest measurable distance, since any attempt to investigate the possible existence of shorter distances, by performing higher-energy collisions, would inevitably result in black hole production.... [from Wikipedia]
It doesn't follow that space isn't continuous, just that our current experiments to probe below that length are expected to create a black hole and change the nature of space in the region.
Best Wishes.
Post by: BilboGrabbins on 15/10/2021 21:47:47
Post by: hamdani yusuf on 16/10/2021 09:43:31
...The Planck length is expected to be the shortest measurable distance, since any attempt to investigate the possible existence of shorter distances, by performing higher-energy collisions, would inevitably result in black hole production.... [from Wikipedia]What prevents us from expanding a 1 meter rod to 1 meter plus half Planck's length, eg. by heating it up?
Post by: Eternal Student on 16/10/2021 23:29:00
What prevents us from expanding a 1 meter rod to 1 meter plus half Planck's length, eg. by heating it up?Are you asking me? BilboGrabbins was the one proposing that space cannot be divided into units smaller than the Planck length.
There's nothing I know of that would prevent space from being continuous. Indeed, the standard formulation of General Relativity requires that space is continuous.
However, when you come to measure a rod there are practical limits in our ability to measure things that accurately. It also assumes the rod is some idealised body and not a quantum mechanical system. Treating the particles that make up the rod as quantum mechanical objects would put a theoretical limit on the ability to localise the ends of the rod.
If I recall correctly, it was this sort of limitation on the ability to localise a particle that lead to the first proposals that space (and time) may not be continuous since it almost becomes irrelevant: You can't localise a particle to one point in space unless it's momentum* → ∞, there is some uncertainty in it's position and therefore there isn't any great difference if you just split space up into discrete intervals rather than assuming it is continuous. However, I prefer to remain open to both possibilities. Space might be continuous or it might be discrete.
From a purely mathematical point of view. We often take derivatives or integrals with respect to some co-ordinate. This Calculus does assume the co-ordinate will be a continuous variable.
Best Wishes.
LATE EDITING: * See comment below by Hamdani Yusuf. "uncertainty in momentum".
Post by: hamdani yusuf on 17/10/2021 07:49:37
You can't localise a particle to one point in space unless it's momentum → ∞It's not the momentum itself that becomes infinite. It's the uncertainty of momentum.
Post by: hamdani yusuf on 01/07/2022 08:53:37
There are many hypercomplex numbers known by modern math. Do they have the same size as real number?
Post by: Bored chemist on 01/07/2022 09:51:35
It's sort of the point here. Physics breaks down below this length.I wonder if Bilbo thinks that physics breaks down for objects smaller than the Planck mass which is about 21 µg
On a day-to-day basis 21µg is a pretty small mass, but it's not impossibly small.
It's about the mass of a million bacteria.
(And I'm still waiting for him to explain what angles I'm not allowed to orient my coffee table.)
Post by: Bored chemist on 01/07/2022 09:59:31
https://twitter.com/pickover/status/1541962088926560256?t=ml0TBOGlhgCZIKDaLXserg&s=03Apparently, the complex numbers have the same cardinality as the reals and I'm tempted to assume that the hypercomplex ones do too.
There are many hypercomplex numbers known by modern math. Do they have the same size as real number?
https://quizlet.com/explanations/questions/show-that-c-the-set-of-complex-numbers-has-the-same-cardinality-as-r-the-set-of-real-numbers-cf3e343a-9b5b-4f78-8a0c-0dcfe9ee5b15
Post by: alancalverd on 01/07/2022 11:09:50
Post by: hamdani yusuf on 02/07/2022 11:38:30
Apparently, the complex numbers have the same cardinality as the reals and I'm tempted to assume that the hypercomplex ones do too.There are as many real numbers in a set of complex numbers where imaginary part is 0. Like wise, there are as many real numbers in a set of complex numbers where imaginary part is 1. You can change the imaginary part with any magnitude. Each of them contains a whole set of real numbers. How can we say that they have one to one relationship?
Post by: Bored chemist on 02/07/2022 11:57:29
Apparently, the complex numbers have the same cardinality as the reals and I'm tempted to assume that the hypercomplex ones do too.There are as many real numbers in a set of complex numbers where imaginary parts is 0. Like wise, there are as many real numbers in a set of complex numbers where imaginary parts is 1. You can change the imaginary part with any magnitude. Each of them contains a whole set of real numbers. How can we say that they have one to one relationship?
Infinite sets are weird.
https://en.wikipedia.org/wiki/Hilbert%27s_paradox_of_the_Grand_Hotel
There are as many even numbers as there are integers (because every even number is twice an integer).
There are as many odd numbers as there are integers (because every even number is twice an integer with 1 added to the product).
There are similarly as many multiples of 3 as there are integers.
Ditto multiples of 4, 5 ... etc.
So the integers are the union of an infinite number of infinite sets sets.
But the cardinality stays the same.
So why would there be a problem with the complex numbers having the same cardinality as the reals?
Post by: hamdani yusuf on 02/07/2022 14:44:01
So why would there be a problem with the complex numbers having the same cardinality as the reals?Why would real numbers have different cardinality than rational numbers?
Where do algebraic numbers belong to?
Post by: alancalverd on 02/07/2022 14:44:40
Post by: Eternal Student on 02/07/2022 15:06:05
Apparently, the complex numbers have the same cardinality as the reals and I'm tempted to assume that the hypercomplex ones do too.Yes, that's correct.
The usual proof uses interleaving of decimal digits to generate a unique real number. Here's an extract that explains it with minimal distraction:
Quote
To show this (a bijection exists between C and R ) you need to show every real number maps to a unique complex number and that every complex number maps to a unique real number. The first part is easy -- every real number already is a unique complex number. So let's concentrate on the second part, mapping the complex numbers to the reals.
Each complex number a+bi, a and b real, may be mapped to a unique real number as follows: Expand a and b as decimals, taking care not to end either in repeating 9s for uniqueness. Then you can interleave the digits of the two decimal expansions so, e.g, the even numbered digits are from a and the odd from b. Start at the decimal points and work out in both directions. Call the result of this interleaving c.
So you now have a real number c from which you can recover a and b, and thus the original complex number a+bi.
Since you did this mapping both ways, by the Cantor-Bernstein theorem (or common sense) the cardinality of the complex numbers and real numbers are the same.
[Quote taken from: https://www.quora.com/Do-the-complex-numbers-have-a-greater-cardinality-than-the-real-numbers ]
The proof requires something like the Schröder-Cantor-Bernstein theorem which means that you do require some of the higher axioms of set theory (e.g. the Axiom of Choice or axioms of logic such as the principle of excluded middles). Wikipedia has some discussion: https://en.wikipedia.org/wiki/Schr%C3%B6der%E2%80%93Bernstein_theorem#Prerequisites . To say that a simpler way, in some systems of mathematics you would not be certain that C and R have the same cardinality.
Anyway, with |R X R| = | R | it would be simple to generalise and show | Rk | = |R| for any natural number k. Since the hypercomplex numbers are elements of a finite dimensional algebra over R, we have that any algebra of hypercomplex numbers would have the same cardinality.
There are as many real numbers in a set of complex numbers where imaginary parts is 0. Like wise, there are as many real numbers in a set of complex numbers where imaginary parts is 1. You can change the imaginary part with any magnitude. Each of them contains a whole set of real numbers. How can we say that they have one to one relationship?Indeed it is weird. It follows from a set of abstract axioms. "Intuitionists" would not accept many of the results concerned with cardinality of infinite sets. As already mentioned, there are systems of mathematics (or axiom schemes) that would not conclude |R| = |C|. If I recall correctly, you ( @hamdani yusuf ) have an interest in Philosophy. You might understand the Wikipedia description of Mathematical Intuitionism better than I do: https://en.wikipedia.org/wiki/Intuitionism.
Best Wishes.
LATE EDITING: Sorry for the overlap. Several new posts have appered since I started writing this. I'll read those in a moment.
Post by: hamdani yusuf on 02/07/2022 15:41:12
There isn't a Mathematics section in this forum. It seemed that the OP was asking something about Mathematics without any reference to some application in Physics.To be clear, I want to discuss pure maths here, unrestricted by physical application. What's important here is the consistency of definitions and relationships among every used concepts in a theory.
Post by: Origin on 02/07/2022 16:06:08
To be clear,Looks like another never ending, merry-go-round thread by Hamdani to put on ignore. Bye and have fun.
Post by: Bored chemist on 02/07/2022 17:10:54
I didn't read the whole thread, but perhaps you could quote the place where somebody asserted that this would be problematic.Here
How can we say that they have one to one relationship?
Post by: hamdani yusuf on 02/07/2022 19:19:08
Since you did this mapping both ways, by the Cantor-Bernstein theorem (or common sense) the cardinality of the complex numbers and real numbers are the same.We can represent any rational numbers by combining two integers as numerator and denominator.
Some irrational numbers can be stated as a rational number powered by another rational number. Let's call them power numbers. How many more expansion procedures like that are required to cover the whole real numbers?
Post by: Eternal Student on 02/07/2022 23:13:29
We can represent any rational numbers by combining two integers as numerator and denominator.
Some irrational numbers can be stated as a rational number powered by another rational number. Let's call them power numbers. How many more expansion procedures like that are required to cover the whole real numbers?
I honestly don't know. It depends what you consider to be an "expansion procedure like that".
For example, would you allow taking limits? If {Xn} is a sequence of numbers you already admit in your set, then why not also include the Real number X whenever the sequence Xn → X. That seems like a reasonable expansion procedure. Anyway, that expansion procedure gets you straight from Q to R in one step.
The old fashioned view is that when trying to build the Real Numbers getting from N to Q is just algebra. You can indeed go a bit further and include some irrational numbers in a field extension of Q if you tried. However, crossing that last mile to build the complete, Archimedian, ordered field we call the Reals steps outside the territory called "Algebra" and into "Real Analysis" (i.e. where things like limits need to be used). It's a bit arbitrary to draw a line somewhere and say this bit and no further is algebra, while that bit over there is analysis but that's what is generally done. I'm mentioning this because you might be considering "an expansion like that" to be some procedure involving only algebra and not analysis: If you denied yourself access to the techniques of Real Analysis then conventional wisdom is that you'll never get to R.
[However, I don't know if anyone was so worried about not crossing that arbitrary line that they really tried hard. I do know that they wouldn't have been able to prove they had got to R - which is mildly amusing. This is because they must demonstrate the field is complete and "completeness" is a property firmly held in Real Analysis territory, so they can't even use those ideas let alone perform some test for it].
Best Wishes.
Post by: hamdani yusuf on 03/07/2022 00:22:27
No one forced you to write in my threads. If you prefer to only read things that already have obvious answers, that's up to you.To be clear,Looks like another never ending, merry-go-round thread by Hamdani to put on ignore. Bye and have fun.
Post by: hamdani yusuf on 03/07/2022 00:27:09
I honestly don't know. It depends what you consider to be an "expansion procedure like that".Adding more members to a set of number by finite amount of additional information.
Post by: hamdani yusuf on 03/07/2022 00:46:24
For example, would you allow taking limits? If {Xn} is a sequence of numbers you already admit in your set, then why not also include the Real number X whenever the sequence Xn → X. That seems like a reasonable expansion procedure. Anyway, that expansion procedure gets you straight from Q to R in one step.I haven't found a reason to deny it.
AFAIK, integers are part of rational numbers, which in turn are part of algebraic numbers, which are part of real numbers. Is there a set of numbers which contains more than algebraic numbers but less than real numbers?
Post by: Eternal Student on 03/07/2022 03:26:19
Is there a set of numbers which contains more than algebraic numbers but less than real numbers?If you just want a SET of numbers, yes, many of them.
There's an infinite set of distinct transcendental numbers, T. These are real numbers that are not algebraic. Actually MOST of the real numbers are these, the algebraic numbers are countable so they are a tiny drop in the ocean compared to the transcendental numbers.
Anyway, you could just keep adding the transcendental numbers one at a time until you got bored.
You can cut down some of those intermediate sets of numbers if you put more of a restriction on your set of numbers. For example, instead of just asking for a set of numbers, insist that the new set of numbers is always a proper Field in its own right. These would be called Field Extensions. (Example: If you try to add π, then the field operations automatically generate π2, π3, ...., 1/π, ...., -π, .... (705 + 3/π), .... so to ensure the set really is closed under field operations you'd need all of these numbers added in one go).
None the less, I still think there's an infinite set of simple field extensions you could find. (I haven't spent too long thinking about it but I reckon you could try a simple field extension by adding π and show that √π is still missing, so extend again with √π and show the √(√π) is still missing..... etc..... the root of what you've just extended with should always be missing).
Best Wishes.
Post by: evan_au on 03/07/2022 07:06:58
Quote
∞∞ = ∞However, 2∞ > ∞
(At least for the counting numbers), so this one seems suspect.
Quote from: Wikipedia
∞−∞ and ∞/∞) are not generally well-defined.In practice, this means that you need more information to determine the answer.
For example, L'Hopital's rule allows you to calculate
Limit of a/b as a→∞ and b→∞
in those scenarios where you know the derivative of a and b (and both aren't infinite).
Post by: hamdani yusuf on 03/07/2022 11:12:13
Quote
https://en.m.wikipedia.org/wiki/Transcendental_number
In mathematics, a transcendental number is a number that is not algebraic—that is, not the root of a non-zero polynomial of finite degree with rational coefficients. The best known transcendental numbers are π and e.[1][2]
Though only a few classes of transcendental numbers are known — partly because it can be extremely difficult to show that a given number is transcendental — transcendental numbers are not rare. Indeed, almost all real and complex numbers are transcendental, since the algebraic numbers comprise a countable set, while the set of real numbers and the set of complex numbers are both uncountable sets, and therefore larger than any countable set. All transcendental real numbers (also known as real transcendental numbers or transcendental irrational numbers) are irrational numbers, since all rational numbers are algebraic.[3][4][5][6] The converse is not true: not all irrational numbers are transcendental. Hence, the set of real numbers consists of non-overlapping rational, algebraic non-rational and transcendental real numbers.[3] For example, the square root of 2 is an irrational number, but it is not a transcendental number as it is a root of the polynomial equation x2 − 2 = 0. The golden ratio (denoted {\displaystyle \varphi }\varphi or {\displaystyle \phi }\phi ) is another irrational number that is not transcendental, as it is a root of the polynomial equation x2 − x − 1 = 0. The quality of a number being transcendental is called transcendence.
Quote
https://en.m.wikipedia.org/wiki/Period_(algebraic_geometry)
The periods are intended to bridge the gap between the algebraic numbers and the transcendental numbers. The class of algebraic numbers is too narrow to include many common mathematical constants, while the set of transcendental numbers is not countable, and its members are not generally computable.
The set of all periods is countable, and all periods are computable,[6] and in particular definable.
Many of the constants known to be periods are also given by integrals of transcendental functions. Kontsevich and Zagier note that there "seems to be no universal rule explaining why certain infinite sums or integrals of transcendental functions are periods".
Quote
https://en.m.wikipedia.org/wiki/Transcendental_function
In mathematics, a transcendental function is an analytic function that does not satisfy a polynomial equation, in contrast to an algebraic function.[1][2] In other words, a transcendental function "transcends" algebra in that it cannot be expressed in terms of a finite sequence of the algebraic operations of addition, subtraction, multiplication, division, raising to a power, and root extraction.[3]
Quote
https://en.m.wikipedia.org/wiki/Computable_number
In mathematics, computable numbers are the real numbers that can be computed to within any desired precision by a finite, terminating algorithm. They are also known as the recursive numbers, effective numbers[1] or the computable reals or recursive reals.
Post by: hamdani yusuf on 03/07/2022 11:43:12
Quote
https://en.m.wikipedia.org/wiki/Continued_fractionRational numbers have finite continued fraction. Irrational numbers, including transcendental numbers have infinite continued fraction.
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on.[1] In a finite continued fraction (or terminated continued fraction), the iteration/recursion is terminated after finitely many steps by using an integer in lieu of another continued fraction. In contrast, an infinite continued fraction is an infinite expression. In either case, all integers in the sequence, other than the first, must be positive. The integers {\displaystyle a_{i}}a_{i} are called the coefficients or terms of the continued fraction.[2]
Post by: hamdani yusuf on 03/07/2022 13:12:23
Quote
https://en.m.wikipedia.org/wiki/Transcendental_numberIt seems like we only need one more step to go from power numbers to transcendental numbers. But not all transcendental numbers can be constructed this way.
In 1900, David Hilbert posed an influential question about transcendental numbers, Hilbert's seventh problem: If a is an algebraic number that is not zero or one, and b is an irrational algebraic number, is ab necessarily transcendental? The affirmative answer was provided in 1934 by the Gelfond–Schneider theorem. This work was extended by Alan Baker in the 1960s in his work on lower bounds for linear forms in any number of logarithms (of algebraic numbers).[18]
Post by: Eternal Student on 03/07/2022 13:25:05
If a is an algebraic number that is not zero or one, and b is an irrational algebraic number, is ab necessarily transcendental?That has a significant copy-and-paste error. ab should be a^b = ab
Best Wishes.
Post by: Eternal Student on 03/07/2022 14:25:44
Here are what I got after go down the rabbit hole.Seems reasonable. For whatever it's worth I didn't know all of the classifications you've managed to find. I have no doubt that there's more ways you could divide up the real numbers. There should be loads of sets of numbers that someone has given a name to and had some passing reason to want to study them.
If you were studying the Real numbers as part of a structured course in Real Analysis, then at about this point people would push your attention to the remarkable facts that do seem to appear:
1. It's very difficult to construct the Real numbers by algebraic methods. (Conventional wisdom is that you can't).
2. However techniques from Real Analysis allow the construction of an object (a complete, totally ordered field extension of the Rationals) that we can call the real numbers.
3. Furthermore, accepting certain axioms, we have a uniqueness property: Any complete totally ordered field extension of the rationals is the same field (up-to isomorphism).
Item 3, the uniqueness property, is oddly reassuring but not necessarily important. It's psychologically reassuring: When Mr. Smith thinks of the real numbers they are using the same thing as Monsieur Smithe except that one says "one", "two", "three" while the other calls it "un", "deux", "trois" etc. It's philosophically reassuring in that perhaps the Real Numbers aren't completely arbitrary or abstract things - there is actually only one thing (up-to isomorphism) that they can be. The uniqueness of the Real Numbers is often the final result or crowning glory presented at the end of an introductory course on Real Analysis, however, I'm not sure it really matters for the purposes of Mathematics. (Maybe it just prevents squabbles among mathematicians claiming that their Real Numbers are better than your Real numbers).
However, 2∞ > ∞Cardinal arithmetic is what they what they sometimes call this. Ummm... I have no idea what else to say but just didn't want you to think your post had gone un-noticed. Thanks @evan_au.
(At least for the counting numbers), so this one seems suspect.
Best Wishes.
Post by: alancalverd on 03/07/2022 15:42:24
If you could divide infinitely, we might ask how would anything get anywhere at a fundamental lengthDangerous use of "fundamental".
The Planck length is the base unit of length in Planck units, just as the meter is in SI units, and it has no special physical attributes.
Unlike the fundamental constants such as e, ε0, μ0 etc which do determine the measured behavior of the universe.
Post by: hamdani yusuf on 03/07/2022 22:08:25
Hi.Thanks for the correction.If a is an algebraic number that is not zero or one, and b is an irrational algebraic number, is ab necessarily transcendental?That has a significant copy-and-paste error. ab should be a^b = ab
Best Wishes.
Now here's an opinion.
If the numerator and denominator are allowed to be infinite, then any real number can be expressed as ratio between two integers with infinite precision. The same thing can't be done for complex numbers or hypercomplex numbers.
Post by: hamdani yusuf on 06/07/2022 15:02:19
I've been feeling the same since the beginning of this thread. So did some critiques of Cantor. Particularly, I'm not convinced by diagonal argument. Eternal Student has shown a loop hole in it. I think it's similar to the cases described in the video below.Quote∞∞ = ∞However, 2∞ > ∞
(At least for the counting numbers), so this one seems suspect.Quote from: Wikipedia∞−∞ and ∞/∞) are not generally well-defined.In practice, this means that you need more information to determine the answer.
For example, L'Hopital's rule allows you to calculate
Limit of a/b as a→∞ and b→∞
in those scenarios where you know the derivative of a and b (and both aren't infinite).
Three false proofs, and what lessons they teach.
Quote
Time stamps:
0:00 - Fake sphere proof
1:39 - Fake pi = 4 proof
5:16 - Fake proof that all triangles are isosceles
9:54 - Sphere "proof" explanation
15:09 - pi = 4 "proof" explanation
16:57 - Triangle "proof" explanation and conclusion
Post by: hamdani yusuf on 06/07/2022 16:11:12
If the numerator and denominator are allowed to be infinite, then any real number can be expressed as ratio between two integers with infinite precision. The same thing can't be done for complex numbers or hypercomplex numbers.I've been thinking through this for quite a while now, but I still can't find a reasonable objection / credible refutation against it. I started to think that the problem is part of information theory, particularly in data compressability. Perhaps it is related to the concept of entropy.
For a start, we can think of integers as part of real numbers which have high compressability, or low entropy. They can be expressed in a finite bits of information, as a multiple of an identity number, which is 1.
Post by: hamdani yusuf on 07/07/2022 04:41:26
For a start,The next step is to fill up the gaps between those integers. The simplest way is by dividing an integer with another integer. We get a rational number.
To express a non-integer rational number, we can use some bits of information as the numerator, some others as denominator, and a few bits for the operator, which is division.
When the numerator and denominator are arranged vertically, the division operator is written as a horizontal line between them. When the numerator and denominator are arranged horizontally, the division operator is written as a diagonal line between them.
For convenience, the denominator can be set as an integer exponent of a base number, usually 10, which is called decimal system. The fractional part is separated from the whole part by a small character. Some regions use comma, while some others use period or dot.
The decimal expression can simplify arithmetic operations like addition and subtraction. But it sacrifices precision, especially if the denominator of the rational number has prime factors other than 2 or 5. But for most practical cases, we don't need infinite precision, hence the rounding error doesn't often cause problems.
Post by: hamdani yusuf on 07/07/2022 09:26:35
It turns out that we can compress the data required to express some irrational numbers if they are algebraic, which is a root of a non-zero polynomial in one variable with integer coefficients. The amount of information needed depends on the coefficients of the polynomial equation.
Post by: Bored chemist on 07/07/2022 10:54:14
When expressed as ratio, 1/2, 1/3, and 1/4 don't seem to need much different amount of information. But when expressed in decimal, 1/3 needs infinite number of digits. Although the decimal digits are repetitive, which make the information compressible.Use base 12 rather than 10.
The problem goes away.
Post by: hamdani yusuf on 07/07/2022 11:52:57
If the numerator and denominator are allowed to be infinite, then any real number can be expressed as ratio between two integers with infinite precision.Like wise, if the degree of polynomial is allowed to be infinite, then any real number can be expressed as a root of polynomial.
Post by: hamdani yusuf on 07/07/2022 11:57:55
But this solution is not general, since it depends on the chosen base number, as well as the denominator. If the denominator has a prime factor not shared with the base number, the number of digits will be infinite.When expressed as ratio, 1/2, 1/3, and 1/4 don't seem to need much different amount of information. But when expressed in decimal, 1/3 needs infinite number of digits. Although the decimal digits are repetitive, which make the information compressible.Use base 12 rather than 10.
The problem goes away.
A more general solution is using continued fraction, which is independent from base number selection.
Post by: Eternal Student on 07/07/2022 15:12:51
Particularly, I'm not convinced by diagonal argument. Eternal Student has shown a loop hole in it.That was an error in the method shown in that particular text (which was a PopSci version of Cantor's proof that ℜ is uncountable ). However, it's possible to fix that and most texts describing the diagonalisation method do exactly that. Just to be clear, the argument is basically sound, it's just that the PopSci article wasn't a perfect version of it.
However, there's no reason why you should go along with it. A lot of people won't like the Axiom of Choice, for example. Earlier posts have mentioned that something like a weak version of this, the axiom of countable choice, does seem to be required. So you can reject the Axiom of Choice and have a perfectly mainstream set theory, or system of mathematics, where Cantor's diagonalisation method would not hold, if you want.
Now here's an opinion.A / B has A as the numerator and B as the denominator.
If the numerator and denominator are allowed to be infinite, then any real number can be expressed as ratio between two integers with infinite precision........ [AND subsequent posts discussing the idea]...
I have no rules to know what to do, or what it means when A or B is infinite.
Presumably you meant A and B are arbitrary Real numbers (and B≠0), they can be big but they are real numbers, so they are never infinite.
Also what do you then mean by "with an infinite precision"?
Does that mean that you can give me the expression A/B to represent the real number √2 and then I can't find any small positive number ξ>0 so that A/B is a distance ξ (or more) away from √2 ?
Best Wishes.
Post by: hamdani yusuf on 08/07/2022 03:02:42
That was an error in the method shown in that particular text (which was a PopSci version of Cantor's proof that ℜ is uncountable ). However, it's possible to fix that and most texts describing the diagonalisation method do exactly that.What should be done to fix it?
Post by: hamdani yusuf on 08/07/2022 03:08:43
A / B has A as the numerator and B as the denominator.I said if numerator and denominator are allowed to be infinite, which means that they don't have to. For example, x=1/3, which can be approximated as 33/100, or more precisely, 3333/10000, or, if you want infinite precision, 333333.../1000000..., with both numerator and denominator have infinitely long digits.
I have no rules to know what to do, or what it means when A or B is infinite.
The numerator can be expressed as
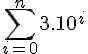, while the denominator can be expressed as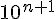 
Both of them are integers, but as n approach infinity, they also approach infinity. But the ratio is finite, and can be expressed as
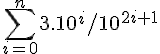
or
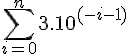
Post by: hamdani yusuf on 08/07/2022 03:50:58
Quote
https://en.wikipedia.org/wiki/Algebraic_numberIf our goal is to fill the gap in real numbers which are not covered by rational numbers (ratio of two finite integers), then algebraic numbers are not well suited for the job for two reasons. First, it can't cover all irrational numbers, such as 2√2. Second, it covers non-real numbers instead, such as 1+i.
An algebraic number is a number that is a root of a non-zero polynomial in one variable with integer (or, equivalently, rational) coefficients. For example, the golden ratio, (1+√5)/2, is an algebraic number, because it is a root of the polynomial x2 − x − 1. That is, it is a value for x for which the polynomial evaluates to zero. As another example, the complex number 1+i is algebraic because it is a root of x4 + 4.
All integers and rational numbers are algebraic, as are all roots of integers. Real and complex numbers that are not algebraic, such as π and e, are called transcendental numbers.
The set of algebraic numbers is countably infinite and has measure zero in the Lebesgue measure as a subset of the uncountable complex numbers. In that sense, almost all complex numbers are transcendental.
Post by: Bored chemist on 08/07/2022 10:21:27
The general solution is to pick a base where the fraction doesn't recur.But this solution is not general, since it depends on the chosen base number, as well as the denominator. If the denominator has a prime factor not shared with the base number, the number of digits will be infinite.When expressed as ratio, 1/2, 1/3, and 1/4 don't seem to need much different amount of information. But when expressed in decimal, 1/3 needs infinite number of digits. Although the decimal digits are repetitive, which make the information compressible.Use base 12 rather than 10.
The problem goes away.
A more general solution is using continued fraction, which is independent from base number selection.
The fact is that you can always do that (and, similarly, you can always choose one where it does).
So whether or not you get a recurring "decimal" isn't important.
It's just an artefact of the arbitrary choice of number base.
Post by: Eternal Student on 08/07/2022 14:36:24
What should be done to fix it? (the diagonalisation method discussed much earlier, e.g. post #14)
Just don't allow the enumeration to contain numbers written with recurring 9 digits. All such numbers can be written with recurring 0 digits instead, insist that this is done.
Example: 0.123999999999....... = 0.12400000000000......
Once you exclude either recurring 9 digits (or recurring 0 digits) then a decimal expansion becomes unique - so that the problem shown in post #14 won't happen.
Best Wishes.
Post by: hamdani yusuf on 08/07/2022 16:01:20
Hi.What if the number is written in binary?What should be done to fix it? (the diagonalisation method discussed much earlier, e.g. post #14)
Just don't allow the enumeration to contain numbers written with recurring 9 digits. All such numbers can be written with recurring 0 digits instead, insist that this is done.
Example: 0.123999999999....... = 0.12400000000000......
Once you exclude either recurring 9 digits (or recurring 0 digits) then a decimal expansion becomes unique - so that the problem shown in post #14 won't happen.
Best Wishes.
Post by: hamdani yusuf on 08/07/2022 16:05:54
The general solution is to pick a base where the fraction doesn't recur.That's an extra work. It's certainly not a practical way to build a computer.
Post by: Eternal Student on 08/07/2022 17:17:14
What if the number is written in binary?That's fine. Then just don't allow recurring 1 digits.
Example: 0.0111111111111111111.... ≡ 0.1 ≡ 0.10000000000000... in binary.
In whatever number base, B, you choose, you just can't allow recurring digits of (B-1). Provided you do this then the representation of a real number as a string of digits is unique.
Best Wishes.
Post by: hamdani yusuf on 09/07/2022 14:11:05
In whatever number base, B, you choose, you just can't allow recurring digits of (B-1). Provided you do this then the representation of a real number as a string of digits is unique.In binary code, the step would remove half of all numbers with finite digits.
Quote
https://en.m.wikipedia.org/wiki/Cantor's_diagonal_argument
In set theory, Cantor's diagonal argument, also called the diagonalisation argument, the diagonal slash argument, the anti-diagonal argument, the diagonal method, and Cantor's diagonalization proof, was published in 1891 by Georg Cantor as a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence with the infinite set of natural numbers.[1][2]: 20– [3] Such sets are now known as uncountable sets, and the size of infinite sets is now treated by the theory of cardinal numbers which Cantor began.
Diagonalization arguments are often also the source of contradictions like Russell's paradox[7][8] and Richard's paradox.[2]: 27
Post by: hamdani yusuf on 09/07/2022 14:13:46
An illustration of Cantor's diagonal argument (in base 2) for the existence of uncountable sets. The sequence at the bottom cannot occur anywhere in the enumeration of sequences above.
The problem with infinite set of natural numbers is that there's no bottom. If we assume the existence of something that is not there, it's no wonder that we will get a contradiction.
Post by: Bored chemist on 09/07/2022 14:35:34
It's certainly not a practical way to build a computer.Had anyone suggested that it was?
Post by: Eternal Student on 09/07/2022 15:35:34
In binary code, the step would remove half of all numbers with finite digits.Why?
Write down a number with finite digits, e.g. 0.10101 . Why would that be removed?
That representation is permitted. (Although during the diagonalisation method you would consider it to have as many 0 digits at the end as required).
Best Wishes.
Post by: hamdani yusuf on 09/07/2022 17:04:57
Hi.Any finite digits binary number can be written in 2 ways. Your restriction rejects one of them.In binary code, the step would remove half of all numbers with finite digits.Why?
Write down a number with finite digits, e.g. 0.10101 . Why would that be removed?
That representation is permitted. (Although during the diagonalisation method you would consider it to have as many 0 digits at the end as required).
Best Wishes.
Post by: hamdani yusuf on 09/07/2022 17:16:47
No. It was to show that your solution can't be both simple and general to make it useful as a tool to solve the problem discussed here, which is the countability of a set of numbers.It's certainly not a practical way to build a computer.Had anyone suggested that it was?
Post by: Bored chemist on 09/07/2022 18:00:22
It's not so much as "solution" as an observation.No. It was to show that your solution can't be both simple and general to make it useful as a tool to solve the problem discussed here, which is the countability of a set of numbers.It's certainly not a practical way to build a computer.Had anyone suggested that it was?
Because you can arbitrarily make any fraction either recur or not (by choosing the number base) there's nothing special about recurring numbers.
So you can simply ignore them.
Ignoring the thing which, at first, looks like an additional complication does make it easier to calculate things.
Post by: Eternal Student on 09/07/2022 18:47:18
Any finite digits binary number can be written in 2 ways. Your restriction rejects one of them.Yes. This is exactly what is required. You want every real number to be uniquely represented.
Best Wishes.
Post by: hamdani yusuf on 29/11/2022 13:58:10
Here is a Venn diagram of real number:
Reference: https://www.physicsforums.com/threads/is-my-classification-of-transcendental-correct.921555
(https://www.physicsforums.com/attachments/b0863664ce8b6788c6c3dbd39245f4d7-png.208105/)
Here's a pattern.
There are infinitely many more integers than natural numbers.
There are infinitely many more rational numbers than integers.
There are infinitely many more algebraic numbers than rational numbers.
There are infinitely many more real numbers than algebraic numbers.
But somehow the state of countability changes only between real numbers and algebraic numbers.
Post by: hamdani yusuf on 29/11/2022 14:12:09
Moreover, at 2:07 rational numbers are classified as countable/list-able using two dimensional list. It's not clear why it stops there, instead of continuing to higher dimensional list/tensor.
Post by: hamdani yusuf on 29/11/2022 14:21:02
is tan(2) transcendental?
the result is transcendental, while it's assumed to be in unit of radians.
the result is unknown, while it's assumed to be in unit of degrees.
I got the same result for sine and cosine.
log(2) is transcendental in base e, but unknown in base 10.
Post by: hamdani yusuf on 30/11/2022 12:55:12
There's also continued fraction to classify subsets of real numbers.We can make a new class of numbers which is a superset of algebraic numbers while being a subset of real numbers. Just like division was used to construct rational numbers, and algebraic functions were used to construct algebraic numbers, we can use a more general operation to construct this new class. Taylor series or generalized continued fraction can be used for this purpose.Quotehttps://en.m.wikipedia.org/wiki/Continued_fractionRational numbers have finite continued fraction. Irrational numbers, including transcendental numbers have infinite continued fraction.
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on.[1] In a finite continued fraction (or terminated continued fraction), the iteration/recursion is terminated after finitely many steps by using an integer in lieu of another continued fraction. In contrast, an infinite continued fraction is an infinite expression. In either case, all integers in the sequence, other than the first, must be positive. The integers {\displaystyle a_{i}}a_{i} are called the coefficients or terms of the continued fraction.[2]
https://en.wikipedia.org/wiki/Taylor_series
https://en.wikipedia.org/wiki/Generalized_continued_fraction#Transcendental_functions_and_numbers
Quote
A generalized continued fraction is an expression of the formFor example,
(https://wikimedia.org/api/rest_v1/media/math/render/svg/dd4d1accb0958ba7af8ab6e9a615ee5168cb28d9)
where the an (n > 0) are the partial numerators, the bn are the partial denominators, and the leading term b0 is called the integer part of the continued fraction.
(https://wikimedia.org/api/rest_v1/media/math/render/svg/79475340ddb27c7c6feb3cfba628f67384c53457)
(https://wikimedia.org/api/rest_v1/media/math/render/svg/87d58af1bad5c08ee378e4648e122117154beba5)
This way, the examples for non-algebraic numbers in the Venn diagram below can be classified as analytic numbers, which means that they can be represented as a regular pattern in a generalized continued fraction. It means that they can be stated using a finite number of bits of information.
Post by: hamdani yusuf on 30/11/2022 13:20:54
Interestingly, all the examples for non-algebraic numbers shown in the diagram above are analytic numbers.
Here is a Venn diagram of real number:
Reference: https://www.physicsforums.com/threads/is-my-classification-of-transcendental-correct.921555
(https://www.physicsforums.com/attachments/b0863664ce8b6788c6c3dbd39245f4d7-png.208105/)
Here's a pattern.
There are infinitely many more integers than natural numbers.
There are infinitely many more rational numbers than integers.
There are infinitely many more algebraic numbers than rational numbers.
There are infinitely many more real numbers than algebraic numbers.
But somehow the state of countability changes only between real numbers and algebraic numbers.
Non-analytic numbers can be constructed by filling ai and bi in a generalized continued fraction with numbers in an irregular pattern, e.g. by putting random numbers for each of them. This makes most of real numbers are non-analytic numbers, i.e. cannot by represented using a finite amount of information.
Post by: paul cotter on 30/11/2022 16:49:44
Post by: alancalverd on 30/11/2022 17:38:59
Post by: hamdani yusuf on 30/11/2022 21:38:33
This way, the examples for non-algebraic numbers in the Venn diagram below can be classified as analytic numbers, which means that they can be represented as a regular pattern in a generalized continued fraction. It means that they can be stated using a finite number of bits of information.This new class of real numbers can also be called compressible number or algorithmic number. They can be produced by a finite algorithm using only natural numbers.
So, the number onion diagram would contain
natural > integer > rational > algebraic > algorithmic > real.
Post by: Eternal Student on 30/11/2022 21:46:32
I quite like a bit of mathematics, so It's nice to see anyone thinking about some Maths on this forum.
Here's a pattern.Sounds OK. Your use of "somehow" makes it sound like it shouldn't happen. Isn't it possible that one of those increases just was much, much bigger than another? The phrase "infinitely many more" just isn't a very restrictive description of an increase in size. There are many increases you can make which are infinite increases in size.
There are infinitely many more integers than natural numbers.
There are infinitely many more rational numbers than integers.
......
But somehow the state of countability changes only between real numbers and algebraic numbers.
Exactly as you have identified, some of those increases leave the end set with the same cardinality as the starting set - but some increases can and do change the cardinality.
But somehow the state of countability changes only between real numbers and algebraic numbers.You may be over-emphasizing exactly where this change takes place. You can add a finite set of transcendental numbers to the algebraic numbers and that's obviously no problem - the final set is still countable. Moreover you can add an infinite BUT countable set of transcendentals to the algebraic numbers and you would still have a final set that is countable. You can keep on adding more infinite (but countable) sets of transcendentals and the resulting set will still be countable. Nothing changes or breaks until you try to add an uncountable set of transcendentals, for example if you tried to add ALL of the transcendental numbers.
To say this a different way, it is not as if the algebraic numbers are the final, last or maximal countable set you could ever build. You can certainly build bigger sets that are still countable. Mathematicians just tend to stop at the algebraic numbers because that's an interesting set of numbers in its own right and not because it was as big as they could get while still keeping the set countable.
You can also play the game from the other end and try to work downwards.... starting from the Reals you can easily strip out an infinite (but countable) set of numbers and you'd still have a set which is uncountable. You can be even more devious and strip out an uncountable set of numbers and yet still have failed to reduce the cardinality (you can still end up with a set this is uncountable).
Somewhere between the algebraics and the Reals, the cardinality jumps from that of N to that of ℜ, but there is no set of numbers that you can identify that describes the maximal countable set or the minimal uncountable set.
Infinity and cardinality, it's an interesting topic.
Best Wishes.
Post by: hamdani yusuf on 30/11/2022 22:56:06
You can add a finite set of transcendental numbers to the algebraic numbers and that's obviously no problem - the final set is still countable. Moreover you can add an infinite BUT countable set of transcendentals to the algebraic numbers and you would still have a final set that is countable. You can keep on adding more infinite (but countable) sets of transcendentals and the resulting set will still be countable. Nothing changes or breaks until you try to add an uncountable set of transcendentals, for example if you tried to add ALL of the transcendental numbers.I'd like to borrow a concept from biology in grouping organisms called monophylecy. A group of numbers worth naming if it's monophyletic.
In your example, they are either polyphiletic or paraphyletic.
Post by: Eternal Student on 01/12/2022 13:28:39
I'd like to borrow a concept from biology in grouping organisms....I expect you can do that.
In your example, they are either polyphiletic or paraphyletic.Maybe but probably only because Human beings tend to start with rational numbers (fractions). Constructing the Real numbers is something mankind and especially mathematicians have been interested in for hundreds if not thousands of years. It's very interesting stuff but we do need to recognise that how things have been done historically does not need to be taken as anything resembling a natural order or evolution. Speaking objectively, Numbers did not come about in just one way, instead human preference has just lead us to develop them one way but other ways are available.
Quite often mankind starts from the counting numbers (the Natural numbers) and historically it was even assumed that these were god-given and could not be constructed from anything simpler. More recently it has been considered that set theory and formal mathematical logic should be the foundation of all mathematics and it is possible to construct the Naturals from these more elementary mathematical objects if you try (see, for example Peano's axioms: http://www2.hawaii.edu/~robertop/Courses/TMP/7_Peano_Axioms.pdf which provides what looks like a fairly nice and short document describing the construction of the Natural numbers. You could also find some details elsewhere like Wikipedia if you wanted but their page(s) are not set up as well for learning). If you wanted an entirely set theoretic approach then you just note that an empty set ∅ should exist in your set theory system and then define the element 0, "zero", (the first Natural number that Peano's axioms requires) to be the empty set ∅. The successor, S(n) can then be defined as the power set of n. For example, the number 1 is defined to be S(0) =def P(∅) =def {∅} where I have written =def to indicate that this is a definition and not to be mistaken as the equality operation = that is defined in the Peano Axioms themselves. Note that although ∅ and {∅} may superficially look to be the same set, they are not. ∅, the empty set, has no elements but {∅} has one element which is the empty set. By continuing to take successors we obtain the number 2 =def {∅, {∅} } which has 2 distinct elements; 3 =def { ∅, {∅}, {{∅}}, {∅, {∅}} } which has 4 distinct elements.... etc.... (it gets messy but you just keep taking power sets).
One way or another, whether god-given or otherwise, we tend to arrive at the Natural numbers as something that is fairly basic and elementary. Where we go from there seems to be just a human preference. Historically, we have tended to construct the rational numbers, "the fractions" a/b and indeed the ancient Greeks were only happy with these. They were greatly troubled about the apparent existence of numbers like √2 which seemed to come out of their knowledge of geometry (e.g. Pythagoras' theorem applied to determine the length of the hypotenuse for a right angled triangle with the two other sides of length 1). However, if you now accept that irrational numbers like √2 are required then there is no reason why you couldn't start to extend the Natural numbers by adding some irrational numbers first rather than by adding some rational numbers.
You can easily have a mathematical structure called a Group where the elements are the Natural numbers plus one or more irrational numbers. Those elements can be combined under the usual operation of addition +.
What I'm trying to say is that it is only human preference that has lead to the development of rational numbers before the development of irrational numbers. In your classification of different sets of numbers as being a "monophylectic" or "paraphylectic", there may not be any objective reason to consider "this place" or "this set of numbers" as being the natural ancestor of some subsequent sets of numbers that we might construct.
To say it another way, when presented with an assorted collection of sets of numbers (e.g. some with Naturals, some with transcendentals, some with a mixture) there may not be any objective way of deciding where their common ancestor might have been and therefore if you have a monophyletic or paraphylectic collection of sets. It's been mainly just human preference that has lead us to think that the natural path of development should be
Naturals ---> Rationals ---> Irrationals ---> Transcendentals ---> Reals
...but all sorts of other development routes are possible, with various branches, forks, re-convergence to a common set and then splitting off again etc. etc.
Naturals ---> Naturals plus √2 ---> Rationals plus √2 ----> Rationals plus √2 and π ---> Reals ----> Complex
\ /\ \
\ / \
\/ / \
Algebraics --------------> Algebraics plus e and Ln 10 \/
Hyperreal
I'm not a philosopher but I'll suggest that Nature didn't evolve the number system down one set route.... it has just always been there and it's only human beings that try to understand it by developing the full system of the Real numbers from simpler structures. There are many routes to get from the Naturals to the Reals and no reason to objectively assert that one is the right way.
Best Wishes.
LATE EDITING: Sorry, the branch diagram for the construction of some sets of numbers only works when viewed on a widescreen monitor with the forum maximised to take up the whole screen. Hopefully you get the idea, even if your small mobile phone device is splitting up the diagram onto many lines. I should have done a proper diagram as a JPEG image or something, sorry.
Post by: Zer0 on 01/12/2022 20:36:00
It's sort of the point here. Physics breaks down below this length.
Reminds me of the concept of Singularities.
P.S. - Perhaps you are Gone, Never to Return...so long & Peace!
✌️
Post by: evan_au on 01/12/2022 21:08:39
Quote from: alancalverd
there are more (numbers) than you could ever need, and they are all freeIn AI (Artificial Intelligence) work, numbers are not free. It takes serious electrical energy to train a large AI model, and even more to run it.
- The more resolution in your calculations (eg using 64 bit floating point instead of 32 point floating point), the faster it converges, but the more electricity it takes to train the model.
- An AI model which is to be used by millions of people (eg a self-driving car algorithm) might use far more electricity to execute than it took to train, so researchers are looking at bringing AI execution down to 16 bits, 8 bits or perhaps even less?
- Some of the recent gaming video chips turned into supercomputers (eg NVIDEA*) have partitioned their computation hardware so it can do 1 x 32-bit operation or 4 x 8-bit operations at once.
..which leads to a debate about "how many numbers do you need?". It's a bit simplisitic to say that the nerves in our brains only have 2 states: firing or not firing.
- There is a complex modulation with rates of firing
- and a poorly-understood overall modulation by brain waves (alpha, delta, etc).
- but rough calculations suggest that neurons on the brain have a marvellous energy economy in terms of energy per transition, which is the envy of engineers designing computers out of silicon...
* other gaming chips are available, and other supercomputers are available, but not many that are both...
Post by: evan_au on 01/12/2022 21:31:57
But even finite numbers can do your brain in. "Graham's Number" is so mind-bogglingly huge that if you tried to hold all the digits of it in your head, your head would collapse into a black hole.
- The proof of this comes from the observation that information has a certain entropy, and the surface of a black hole is the smallest area with a certain entropy
- Apparently, the Schwarzschild radius of Graham's number is bigger than your head... (Note: I haven't tested this calculation myself)
https://en.wikipedia.org/wiki/Graham%27s_number
Podcast (1 hour:15 minutes): https://www.preposterousuniverse.com/podcast/2022/10/17/214-antonio-padilla-on-large-numbers-and-the-scope-of-the-universe/
Post by: Eternal Student on 02/12/2022 01:58:45
I've enjoyed reading @evan_au 's comments and might get around to listening to that podcast. It has also reminded me of something else that was relevant from an older comment by @hamdani yusuf .
It means that they (...certain types of numbers...) can be stated using a finite number of bits of information....(and going on to suggest that other types of numbers can not be represented with a finite amount of information)....
Any number can be represented with a finite amount of information or digital bits of information. It's just that you can't have this ability for all numbers simultaneously. Let's try and explain this simply and without recourse to much mathematics:
Let's take Graham's number as our example, that can be taken as your standard unit for quantity. So you just set one bit for a quantity equal to Graham's number. This means you can also represent some other numbers (like two lots of Graham's number) quite easily. However, a small number like 1, then needs to be expressed as a fraction of Grahams number and that is now going to be extremely information dense.
To re-phrase the concept in more conventional mathematical language, we can always perform a change of basis so that any number can be easily represented.
Anyway, it's just my opinion but I would say that as human beings we are all too quick to assume that some numbers intrinsically have weird or interesting properties as if that is a property of the number. Quite often it is just a property of the representation we are using.
Best Wishes.
Post by: hamdani yusuf on 02/12/2022 02:43:58
What I'm trying to say is that it is only human preference that has lead to the development of rational numbers before the development of irrational numbers. In your classification of different sets of numbers as being a "monophylectic" or "paraphylectic", there may not be any objective reason to consider "this place" or "this set of numbers" as being the natural ancestor of some subsequent sets of numbers that we might construct.In the Venn diagram shown below, smaller ellipses are subsets of the larger ellipses. Algorithm to precisely express the numbers in smaller sets are more restricted compared to larger sets.
Algorithm allowed to express natural numbers only involve addition and multiplication of smaller natural numbers.
Algorithm to express integer numbers requires subtraction operator, besides addition and multiplication of natural numbers.
Algorithm to express rational numbers requires division operator, besides what's needed to express integer numbers.
Algorithm to express algebraic numbers requires root operator, besides what's needed to express rational numbers.
Algorithm to express algorithmic numbers requires finite algorithm, besides what's needed to express algebraic numbers.
The non-algorithmic real numbers can't be expressed using finite algorithm.
You can't jump to use root operator for the first iteration of number classification because it requires exponentiation by rational number.
(https://www.physicsforums.com/attachments/b0863664ce8b6788c6c3dbd39245f4d7-png.208105/)This way, the examples for non-algebraic numbers in the Venn diagram below can be classified as analytic numbers, which means that they can be represented as a regular pattern in a generalized continued fraction. It means that they can be stated using a finite number of bits of information.This new class of real numbers can also be called compressible number or algorithmic number. They can be produced by a finite algorithm using only natural numbers.
So, the number onion diagram would contain
natural > integer > rational > algebraic > algorithmic > real.
As I mentioned earlier, all examples above are algorithmic numbers. Non-algorithmic numbers can't be accurately expressed using finite algorithmic symbols.
Post by: Eternal Student on 02/12/2022 04:44:58
You can't jump to use root operator for the first iteration of number classification because it requires exponentiation by rational number.Not necessarily.
For example, the Taylor series for √(1+x) is just a series involving only exponentiation by natural number powers (which is just repeated multiplication if you didn't even want to use that exponentiation). Admittedly, I would like some use of division. Anyway set x = 1 and then you have a series which can be the motivation for them wanting to build a bigger algebraic structure that includes the limit of that series. (Just to be clear, they don't need to know anything about Taylor series - they can just observe that there is a series which seems to be leading somewhere and be motivated to build a bigger algebraic structure that would include the limit of such a series).
Best Wishes.
Post by: evan_au on 02/12/2022 08:18:53
Quote from: hamdani yusuf
You can't jump to use root operator for the first iteration of number classification because it requires exponentiation by rational number.From another perspective, there is a binary square root algorithm that operates very similar to binary division - just compare, subtract and shift.
- It requires no exponentiation.
- However, since it requires an infinite number of shifts and subtractions to calculate √2, you can't call it a finite algorithm.
- ...even if you did have a computer that could store and compare numbers with an infinite number of bits.
Post by: hamdani yusuf on 02/12/2022 10:20:30
Hi.Thanks for the correction.You can't jump to use root operator for the first iteration of number classification because it requires exponentiation by rational number.Not necessarily.
For example, the Taylor series for √(1+x) is just a series involving only exponentiation by natural number powers (which is just repeated multiplication if you didn't even want to use that exponentiation). Admittedly, I would like some use of division. Anyway set x = 1 and then you have a series which can be the motivation for them wanting to build a bigger algebraic structure that includes the limit of that series. (Just to be clear, they don't need to know anything about Taylor series - they can just observe that there is a series which seems to be leading somewhere and be motivated to build a bigger algebraic structure that would include the limit of such a series).
Best Wishes.
But still, the main point remains. You can't jump number classifications.
Admittedly, I would like some use of division.Which is multiplication by rational numbers.
Post by: hamdani yusuf on 02/12/2022 10:29:49
Shift left is related to multiplication, while shift right is related to division.Quote from: hamdani yusufYou can't jump to use root operator for the first iteration of number classification because it requires exponentiation by rational number.From another perspective, there is a binary square root algorithm that operates very similar to binary division - just compare, subtract and shift.
- It requires no exponentiation.
- However, since it requires an infinite number of shifts and subtractions to calculate √2, you can't call it a finite algorithm.
- ...even if you did have a computer that could store and compare numbers with an infinite number of bits.
Infinite sum can be expressed using finite algorithm, as long as it follows a regular pattern.
(https://wikimedia.org/api/rest_v1/media/math/render/svg/f9131e72da836fa3cfe2a45bd7e91166d71e1984)
(https://wikimedia.org/api/rest_v1/media/math/render/svg/b23f95e353c790da794dc78a840d98072b1a46a5)
Post by: Eternal Student on 02/12/2022 20:28:03
But still, the main point remains. You can't jump number classifications.We can. Since we already know the Reals exist or can be constructed by some route, we can just introduce an element √2 and describe how it combines with the Naturals under addition as an axiom. We don't have to tell them (or ourselves, or whoever it was constructing the Reals by some other route) how or why they might generate that number or want to build a bigger algebraic structure that includes that element just from stuff they notice from the numbers they already have.
If the axioms are consistent with how we already know that √2 behaves in the Reals (e.g. 3 + (2+√2) + (4+√2) = (9 + √2) + √2 etc. etc. - you just tell them exactly how the new element should combine and behave) then the structure they build will be a copy of what we would describe as the Group generated by N and √2. (Specifically, since those axioms were consistent with and necessarily follow from what we know already about the Reals, we do no harm by adding those axioms. We don't produce any new inconsistencies and we don't give them access to any logical statements that we don't have access to ourselves).
I appreciate that this may not be your (or many people's) idea of a natural route for the evolution or development of the Reals from the Naturals. It only seems "natural" if there was some reason or motivation to build a bigger algebraic structure based on what you can see emerging or generate from the numbers you already have. However, from a pure Mathematics point of view, it is possible to create a structure like this regardless of whether you could see any reason to incorporate such an element that behaves √2. Our own historical development of the number system progressed in various ways, sometimes there were clear reasons for wanting to include a new element and it was very much as if you could almost generate that number from what you already had. However, sometimes you couldn't generate anything like that element from what you already have but there was still some reason to want to include a new thing you could call a number that had a particular property. Here are some examples:
Example 1: The need for irrational numbers like √2 was first suggested by some results from geometry. It wasn't until much later that results like Taylor series were known and you can then see that we can almost generate the new number from what you already have.
Example 2: The complex numbers can be developed literally just by taking as an axiom that we want a new element i and the properties that this should have under the field operations of + and x. We take as an axiom that this element has an interesting property under multiplication, i2 = -1 even though no other element we already had in the Reals has any ability resembling this. We didn't (and can't) obtain anything like the element i just by taking some sequence or series of real numbers and considering limits. I haven't tried but I would say that we can't obtain the element i by anything that looks like a simple extension of some algorithm or process applied to elements of ℜ. Whether we can or not, I can assert that we just didn't do it that way. We identified such an element i as being desirable and wished to construct an algebraic structure that behaved like a number system (a field) with that element for a different reason. We just wanted a field where equations like x2 +1 = 0 had a solution and the earliest development of the Complex numbers was entirely based on just assuming the existence of a number which will do the job. Where Complex numbers are still studied at school (which I think is now only on some further maths A-level courses) this is still exactly how they present the Complex numbers - you just start by assuming the existence of a number i with the property i2 = -1.
Now, as it happens, we certainly don't just have to take the existence of i as an axiom. We can construct a field based on the structure ℜ X ℜ with field operations + and x defined a certain way. You don't generally see that being presented until University level studies to the best of my knowledge. However, it's just worth noting that it can be done. It may seem odd if historically someone had just started the other way round but it is entirely possible that they could have done so.... "Look here's an algebraic structure we can build". People would have said "...and why would we want that? I can build a garden spade that also has a drinking trough for camels but we will never want it". However, some years later the original person can reply "ah ha... the thirsty camel has finally come while you were gardening... or in my case I have an element (0,1) such that (0,1)2 = (1,0) and that's precisely what we need for the element i".
Anyway... this post is getting too long. The gist of it is... crumbs, I can't remember, it was a sort of ramble about number systems and camels... oh yes, vaguely the development of the number system progresses in all sorts of ways. You don't always need to identify how you might generate a new number from what you already have, sometimes you will just identify a need for such a new number (like i ) and chose to extend your algebraic structure, your number system, to include it. A set of space aliens may have developed a new element √2 that they wanted to include with their Natural numbers perhaps because an equation like x2 - 2 = 0 was very important to them.
Best Wishes.
Post by: hamdani yusuf on 03/12/2022 05:18:10
Integers are naturally formed by inverse operator of addition.
Rational numbers are naturally formed by inverse operator of multiplication.
Algebraic numbers are naturally formed by inverse operator of exponentiation.
Following the pattern, it seems possible to construct higher class of numbers using higher level of operations, and use their inverse.
Post by: hamdani yusuf on 14/12/2022 22:19:38
Quote
In mathematics, the hyperoperation sequence [nb 1] is an infinite sequence of arithmetic operations (called hyperoperations in this context)[1][11][13] that starts with a unary operation (the successor function with n = 0). The sequence continues with the binary operations of addition (n = 1), multiplication (n = 2), and exponentiation (n = 3).Hyperoperations allow us to exactly express a non-algebraic real number.
After that, the sequence proceeds with further binary operations extending beyond exponentiation, using right-associativity. For the operations beyond exponentiation, the nth member of this sequence is named by Reuben Goodstein after the Greek prefix of n suffixed with -ation (such as tetration (n = 4), pentation (n = 5), hexation (n = 6), etc.) [5] and can be written as using n − 2 arrows in Knuth's up-arrow notation.
For example, x^x=2.
According to Wolframalpha, x=e^(W(log(2)). It involves inverse of tetration.
More real numbers can be constructed using inverse of pentation, hexation, and so on.
Post by: hamdani yusuf on 18/12/2022 10:56:41
Start from H1, which is addition, we can expand natural numbers to integers by adding negative integers. Here's an example.
x+10 = 1
In Hyperoperation notation,
x (H1) 10 = 1
x = -9, which is not a natural number.
Next is H2, which is multiplication. We can expand integers to rational numbers by adding fractions. Here's an example.
x * 10 = 1
In Hyperoperation notation,
x (H2) 10 = 1
x = 0.1 which is not an integer.
Post by: hamdani yusuf on 24/12/2022 11:15:07
x ^ 3 = 2
In Hyperoperation notation,
x (H3) 3 = 2
There are 3 solutions for x.
x=2^(1/3) ≈ 1.2599
x=(-1 - i√3)/(2^(2/3)) ≈ -0.62996 - 1.09112i
x=(-1 + i√3)/(2^(2/3)) ≈ 0.62996 + 1.09112i
None of them are rational number.
What we usually call algebraic numbers are finite additions of one or more root numbers which have 0 imaginary component, or 0 argument in polar coordinate.
For example, 1+√2 cannot be expressed as a simple root number, which can be turned to an integer by raising it to the power of a rational number.
Post by: hamdani yusuf on 26/12/2022 07:53:28
plot x^(x^x) - 2
https://www.wolframalpha.com/input?i=plot+x%5E%28x%5Ex%29+-+2
plot( x^x)^x - 2
https://www.wolframalpha.com/input?i=plot%28+x%5Ex%29%5Ex+-+2
If the brackets are omitted, Wolframalpha seems to evaluate the equation from the right most exponentiation first.
Post by: hamdani yusuf on 12/06/2023 08:02:41
Quote
There's a strange number system, featured in the work of a dozen Fields Medalists, that helps solve problems that are intractable with real numbers.I'm wondering if this number system can help solving the problem here called "the continuum hypothesis conundrum".
Post by: hamdani yusuf on 12/06/2023 08:07:28
How to Wrangle Infinity (an intro to p-adic numbers)
Intuition for the p-adic metric
Post by: Zer0 on 18/06/2023 21:31:52
As the Topic of the thread is 0...
I was Wondering..
Are there any fields of knowledge in which 0 is attributed a (+) or (-) sign?
Have you ever come across a +0 or -0 value?
Thanks!
Post by: hamdani yusuf on 19/06/2023 01:56:34
If you don't mind, i have a small query.I've seen them used in the study of limits.
As the Topic of the thread is 0...
I was Wondering..
Are there any fields of knowledge in which 0 is attributed a (+) or (-) sign?
Have you ever come across a +0 or -0 value?
Thanks!
Post by: hamdani yusuf on 29/01/2024 04:18:48
What we usually call algebraic numbers are finite additions of one or more root numbers which have 0 imaginary component, or 0 argument in polar coordinate.The argument in polar coordinate can also be π to make the number real.
Post by: hamdani yusuf on 29/01/2024 04:48:12
Math Has a Fatal FlawAccepting the validity of diagonalization method comes with the cost of flawed and broken math. The diagonalization method contains loop holes like what we find in "proof" demonstrating that 1=2.QuoteNot everything that is true can be proven. This discovery transformed infinity, changed the course of a world war and led to the modern computer.The video title sounds bombastic, perhaps deliberately to increase views.
IMO, the paradox and confusion comes from how we treat infinity.Quotehttps://brilliant.org/wiki/infinity/
Infinity is the concept of an object that is larger than any number. When used in the context "...infinitely small," it can also describe an object that is smaller than any number. It is important to take special note that infinity is not a number; rather, it exists only as an abstract concept. Attempting to treat infinity as a number, without special care, can lead to a number of paradoxes.
Infinity is not a number!QuoteBecause infinity is not a number, it requires special rules of arithmetic in order to remain consistent. This is a useful view in fields such as measure theory, which extends the real numbers by adding two numbers ∞ and −∞, that satisfy some additional rules:
a+∞ = ∞+a = ∞ (for any a besides −∞)
a−∞ = −∞+a = −∞ (for any a besides ∞)
a⋅∞ = ∞⋅a = −∞ (for positive a)
a⋅∞ = ∞⋅a = −∞ (for negative a)
a/∞ = a/-∞ = 0 (for real a)
∞/a = ∞ (for positive a)
∞/a = -∞ (for negative a)
It is worth noting that 1/0 is not ∞. Additionally, operations involving multiple infinities (such as ∞−∞ and ∞/∞) are not generally well-defined.
Importantly, note that this is an extension of the real numbers chosen specifically to allow infinity to be treated as a number; without this context, infinity remains a concept rather than a number. For instance, the following sections continue to treat infinity as a concept rather than a number, because the measure theory context above no longer applies
Post by: hamdani yusuf on 31/01/2024 00:00:34
Post by: hamdani yusuf on 31/01/2024 13:20:31
Any number can be represented with a finite amount of information or digital bits of information. It's just that you can't have this ability for all numbers simultaneously.I don't think it's true. If a number has infinitely long digits with no algorithm to express those digits, it cannot be represented with a finite amount of bits. Algorithmic numbers can be represented with a finite amount of information. They are essentially compressible numbers. On the other hand, non-algorithmic numbers are incompressible. There are infinitely many more incompressible numbers than compressible numbers.
Post by: Origin on 31/01/2024 16:40:26
Post by: paul cotter on 31/01/2024 16:47:31
Post by: hamdani yusuf on 31/01/2024 21:25:25
Have you found an answer to the question "how many numbers exist"?Yes, it's infinitely many.
Infinity itself is not a number. It's an abstract concept. Treating it as a number like what Cantor did led to contradictions.