Naked Science Forum

On the Lighter Side => New Theories => Topic started by: talanum1 on 20/03/2022 11:57:03

Title: Is ζ(-1) = -1/12 Inconsistent?
Post by: talanum1 on 20/03/2022 11:57:03

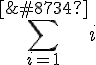The result of = ∞ is inconsistent with ζ(-1) = -1/12. One can write this as: 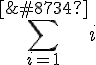not = ∞. Clearly an inconsistency! (Where [&#8734?] = ∞).

I saw a video where they happily plough with the contradiction.

Title: Re: Is ζ(-1) = -1/12 Inconsistent?
Post by: Bored chemist on 20/03/2022 13:13:20

Quote from: talanum1 on 20/03/2022 11:57:03

I saw a video

Have you a link?

Title: Re: Is ζ(-1) = -1/12 Inconsistent?
Post by: talanum1 on 20/03/2022 13:37:05

Yes:

at timestamp: 35:28.

Title: Re: Is ζ(-1) = -1/12 Inconsistent?
Post by: talanum1 on 20/03/2022 14:06:25

This must have to do with analytic continuation of ζ(s). Can you call it analytic continuation if the continuation contains an expression with a pole in it?

Title: Re: Is ζ(-1) = -1/12 Inconsistent?
Post by: talanum1 on 21/03/2022 09:33:27

We must find the source of the inconsistency.

Title: Re: Is ζ(-1) = -1/12 Inconsistent?
Post by: Origin on 21/03/2022 11:32:07

Quote from: talanum1 on 21/03/2022 09:33:27

We must find the source of the inconsistency.

You should go ahead and find the source and then let us know.
Thanks.

Title: Re: Is ζ(-1) = -1/12 Inconsistent?
Post by: talanum1 on 22/03/2022 11:03:13

The source is: ζ(s) is just defined for Re(s) > 1, so we can simply not believe: .
 ([&#8734?] = ∞)

Title: Re: Is ζ(-1) = -1/12 Inconsistent?
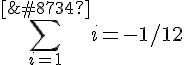Post by: Origin on 22/03/2022 16:19:23

Quote from: talanum1 on 22/03/2022 11:03:13

The source is: ζ(s) is just defined for Re(s) > 1, so we can simply not believe: .
 ([&#8734?] = ∞)

Thanks for finding the source.  So, I guess we are done here.

Title: Re: Is ζ(-1) = -1/12 Inconsistent?
Post by: talanum1 on 13/05/2022 13:24:50

We have ς (s) only defined for Re(s) > 1, and analytic continuation says: assign some values for ς(s) for Re (s) <= 1 that analytically follows from it's value for Re (s) > 1. These values are wholly determined from it's values for Re(s) > 1, so they need not be the same as expected from the definition of ς (s). We must take these values as an (inconvenient) fiction.

Title: Re: Is ζ(-1) = -1/12 Inconsistent?
Post by: Eternal Student on 13/05/2022 18:00:34

Hi.

The last post seems to have the right idea (minor issues with the way you phrased it - but that's not important).

Quote from: talanum1 on 13/05/2022 13:24:50

We have ς (s) only defined for Re(s) > 1

    It's only defined as  ζ(s)  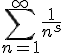=       when   Re(s) >1.         That's what I think you meant.

Quote from: talanum1 on 13/05/2022 13:24:50

We must take these values as an (inconvenient) fiction.

  ?  They are something but they aren't the infinite sum of the same series described above,  if that's what you meant.

Best Wishes.