Post by: Eternal Student on 02/05/2022 17:26:11
I've been reading a bit more stuff about classical elctro-magnetic fields. There is supposed to be energy contained within a E field (and a B field, or both together). An alternative way of describing the same energy can also often be made. For example if two charges are in close proximity, then you can describe the energy as being stored "in" the separated charges.
Anyway, I'm once again interested in where this energy really is and how it behaves:
If a particle has a charge then it creates an electric field. If that energy is in the particle, then it would probably contribute to the total mass of the particle. On the other hand if that energy is actually spread out over all space and contained in the electric field then it may not contribute to the mass of the particle.
Hence, the main question: Does charge contribute to mass?
Examples: 1. There seems to be a difference in mass between electrons and neutrinos, although that's complicated because neutrinos aren't exactly uncharged versions of electrons.
2. Imagine a small spherical conductor, which we will consider as our "particle". Rub the thing with some fur to put a charge on it. Has the mass of the spherical conductor changed? Will it have more inertia? Is this change purely because several thousand electrons were added to the spherical conductor and each electron had mass? Let's try a similar idea - transfer 1800 electrons to the conductor and remove 1 proton from it (i.e. the mass of electrons as you would measure it if you separated them, you know - took them off to infinity and then measured the mass there - should match the mass of the proton when similarly separated). Anyway, the idea being that the overall charge on the spherical conductor should now be -1801 ( -1800 from the electrons and -1 by removing a proton), so it is charged but the separately measured mass of what you've added and taken away shows no overall change. Would there still be a change in the mass of the spherical conductor?
Best Wishes.
Some references, if you want them. I'm going to hide them under this spoiler because it helps to keep the main post short:
Spoiler: show
Best Wishes.
Post by: Halc on 02/05/2022 17:48:31
For example if two charges are in close proximity, then you can describe the energy as being stored "in" the separated charges.It seems not to be 'in' any particular place/object/field, similar to the discussion about the mass of an object increasing at higher altitudes. The energy of the rock/Earth system is up, along with the system mass, but that mass is added to the system, not necessarily the Earth, rock, both, or the gravitational field.
Anyway, I'm once again interested in where this energy really is and how it behaves:
Similarly, a system of two stationary protons in close proximity (not too close) has more energy than the same situation with greater separation, but it is probably a mistake to say that energy is in the protons or the field or whatever.
Quote
Hence, the main question: Does charge contribute to mass?System mass, not field energy or particle energy. Is charge of one particle 'energy'? Only way I can get energy from that is to introduce a 2nd particle, also charged, at which point the energy is a function of their separation.
Didn't yet read the spoiler. Your 'rubbed balloon system' charged with the 1800-1 arguably has more mass because all those extra electrons have been brought into proximity to each other, which is energy that can be harvested. It took work to put them there.
Post by: Eternal Student on 02/05/2022 23:57:37
LATE EDITING: This post has been shortened but is still too long and definitley not urgent.
It seems not to be 'in' any particular place/object/field, similar to the discussion about the mass of an object increasing at higher altitudes....(and following comments)...Yes, that was my thinking. I'm looking over all the similar situations just to check it does all make sense. It does no harm to re-examine my own pre-conceived ideas and I'm keen to get some opinions and see what I might be missing completely.
Just to be clear, I wasn't the one who said energy is stored "in the field". That does seem to be the phrase used in many texts on the subject. I do think the whole situation about "energy" is complicated and I don't claim to understand what energy or mass is. For the moment I'm going along with the idea that it might be contained "in the field" as many texts suggest and just seeing what consequences follow from that.
For a simple electric circuit component, e.g. a Capacitor, there is energy stored in the capacitor when it is charged. ½CV2 with C = capacitance and V = Voltage across the plates. That formula can be determined by various methods. You can recover that energy easily enough by allowing the capacitor to discharge into an electrical circuit.
In this simple example, the energy contained within the capacitor is precisely equal to the result you obtain by taking the E field of the entire universe and computing the integral over all the space in the universe of (constants times by) |E|2 when it was fully charged and then subtracting the same "all of space integral" for the E field when the plates are discharged.
An ideal capacitor is simple because you can assume the electric fields they generate are entirely contained within the component, specifically between the two plates, so that's going to be the only bit of space where the E field changes just by allowing the component to discharge. The integral is then simple.
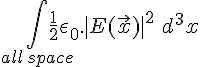= [Rest of space contribution] + ½ξ0 . |E|2 .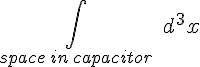 
NOTE that the E field between ideal capacitor plates is uniform (constant) and can be taken out of the integral as shown. The integral is then trivial, it's the volume of space between the plates. Simple substitution with Capacitance C and Voltage across the plates V, shows the RHS becomes [Rest of Space contribution] + ½CV2.
The [Rest of space contribution] never changes because the E field never changes there just by charging or discharging the capacitor. So the energy change due to charging or discharging the capacitor is precisely equal to the energy change in the E field over all of the universe.
CAVEATS: The [Rest of space contribution] may not be finite or a well defined definite integral in the real world. As in other areas of physics, we can just assume it is "something" and provided we subtract exactly the same thing, then it's gone. Alternatively, we can work entirely within an idealised almost empty universe. The only things in that universe need to be the capacitor and the circuit to allow it to discharge, the scientists doing the experiment... and that's about all.... In our simple model universe, we'll assume the same laws of physics hold and since all E fields from any source will fall off as 1/r2 that integral will certainly be finite in that model universe.
I have probably laboured the point a little and almost exactly this calculation was done in one of the references given earlier (or in most good textbooks on electrodynamics). However, it just is absolutely incredible and well worth spending a moment to consider, in my opinion.
You might think it only works for an ideal capacitor but that's not the case: You get the same results by considering the energy stored in an inductor (or "coil") but this time its in the magnetic field. At least in these two simple examples (capacitor and inductor) the change in the fields is entirely confined to one region of space (the interior of the component) and I would fully expect those components to mass more when they are charged (or have current flowing in them for the inductor). There seems to be an easily identified, spatially finite system, that has some (extra) mass due to this energy density existing.
What would be more remarkable is if this result holds for an arbitrary assembly of charges, i.e. if there is energy contained in the E field around every point charge. It suggests that some of what we might call "mass" for a charged particle may not even be local to the point charge. Moving the charge around effectively re-shapes the E field throughout the universe, so it is possible that some spatially remote energy density (i.e. some "mass") might be effectively dragged around with the particle. This additional inertia might be noticed at the point of contact of the applied force on the charged particle. To say that another way, you might be able to change the inertial mass of a point charge just by changing the permittivity constant of some part of space that is a distance away from the point charge. I honestly don't know.
This post is too long and additional comments have been removed in late editing.
Best Wishes.
Post by: paul cotter on 03/05/2022 20:42:12
Post by: Eternal Student on 03/05/2022 22:12:33
Thanks for your comments @paul cotter .
If you put a resistive load across the cap, you only get half the stored energy, regardless of the value of said resistor.That one I would disagree with. It may take forever to get all the power out of the capacitor but it will eventually become heat in the resistor.
Everything else seems reasonable...
..to charge a capacitor through a resistor...would lose some energy in the resistor etc.
Best Wishes.
Post by: evan_au on 03/05/2022 22:29:18
Quote from: Paul cotter
to charge a capacitor through a resistorThat's why electric vehicles use electronic DC-DC converters to extract charge from the battery, and apply power to the electric motor (and the reverse when braking).
With the DC-DC converter, you can take one voltage and turn it into a different voltage, with quite high efficiency (up around 90%), compared to the significant losses you would get from trying to reduce the voltage with a resistor (and when braking, the DC-DC converter can turn a low voltage into a higher voltage to recharge the battery, which a resistor can't do!).
See: https://en.wikipedia.org/wiki/DC-to-DC_converter#Electronic_conversion
Post by: paul cotter on 04/05/2022 10:24:40
Post by: Eternal Student on 04/05/2022 11:11:52
It doesn't matter - but if you want to use equations there are two reasonable ways it can be done:
1. Create your equations in whatever system you prefer. Simply take a picture of it, for example take a screenshot or use the "snipping tool". Then add that as an attachment in the forum post.
Inserting pictures can be a bit fiddly if you want them in the middle of other text but it is possible (try it out sometime). To start with it's easier to just leave it at the bottom of the post and leave it as an attachment - people can click on it if they want to.
2. Use LaTex. The forum supports LaTex reasonably well. What you do is enclose your LaTex within start and end tags. You'll pick up the idea fairly quickly. To get started there are some buttons with some pre-prepared common LaTex code.
Here's an example:
[ Invalid Attachment ]
Click the button with the definite integral and this piece of LaTex code jumps into your post:
Code: [Select]
[tex]\int_1^\infty\frac{1}{x^2}\partial x[/tex]
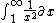
LaTex guides are available in all sorts of places online. If you ever want a particular symbol, Google will usually find the right instruction or code for you quickly.
Notation like x^2 will be printed (or rendered) as x2. Meanwhile x_3 produces subscripts like x3. Anything with a \ symbol (often called "backslash") at the front produces a special symbol. For example \int produces an Integral symbol.
Experiment with changing the pre-assembled bits of LaTex code available from those buttons and you'll soon start picking up how it works.
Let's say you didn't like the pre-assembled integral from 1 to infinity of 1/x2 but instead wanted an integral from 0 to 5 of x3. make the following changes to the code shown earlier:
Code: [Select]
[tex]\int_0^5 x^3 dx[/tex]
Which should produce this:
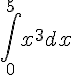
As with all things, you can't learn it all in 5 minutes but the pre-assembled code available from the buttons will help you mark up a few things fairly quickly if that's all you need.
Best Wishes.
Post by: Eternal Student on 04/05/2022 13:56:16
You Tube was recommending a new video to me yesterday. It's related to the ideas in this thread, Energy being contained in the E field.
There are two videos by Veritasium about what actually transmits the energy in electrical circuits, available on You Tube. WARNING: They are not short. If anyone is interested but still uncertain that there might be energy contained in the E field, it's definitely worth watching, i.m.o. I would say watch the first video first - but time is precious, it's more efficient to skip straight to the second video.
The original video is here:
This one is the latest and addresses some inaccuracy in the first video:
- - - - - - - - - - - - -
You don't have to watch the videos (obviously). I'm just going to take the liberty of claiming that the idea that Energy is contained in the E field and spread out throughout all of space is an extremely powerfull idea.
It's causing me to question again what we consider "energy" to be and what we consider to be "mass". So I'm going to repeat my original question from the start of this thread:
Does charge contribute to mass?
There seems to be Energy density in the E-field created by a charge, leading to the possibility that (for some assemblies of charged particles), some of the inertial mass of that assembly is not confined to a finite region of space that you might call the location of that system or assembly - but instead it is spread out across all of space.
What difference could this make and/or how could you determine that some of the inertial mass of the assembly is non-local to the assembly?
You could flood a region of space away from the assembly with a suitable di-electric material. This will change the permittivity, ε, of a volume of space. Energy density of the E-field in space = ½. ε . |E|2, so that is is very likely to change when ε changes. That may influence the resistance to an applied force (the inertial mass) that you notice when a force is applied to the assembly of charges.
Alternative experimental setup's are possible. For example, you can build a Faraday cage and just use that to keep the E field in a region of space down to 0 close to the assembly. You should also get a similar effect by putting the charged assembly inside the Cage and grounding the outside of the cage (i.e. attempt to limit the amount of space available for the E-field from the charged assembly).
Practical problems presumably exist - for example the sort of charged particle I'm imagining would be something like an electron, so that its charge would be significant compared to its mass. How you attempt to push that electron with a force is a problem since we would usually use an E field for that but we don't really want to mess with the E-field again, so we'd be wanting something more like a thin stick to poke it with. (My hand-eye co-ordination isn't that good these days).
Anyway, if anyone knows of a similar experiment that has been done and/or a good reference for this sort of thing, please let me know.
Meanwhile, I'll console myself with the idea that although E fields are interesting, they remain only an approximation to what is happening. There may not be any E field that exists throughout all of space. It's all a classical not a quantum theory and Q.F.T does not need an E field, for example.
Best Wishes.
Post by: paul cotter on 04/05/2022 15:10:42
Post by: Eternal Student on 05/05/2022 03:48:41
@paul cotter , there's no requirement to watch any videos. I suppose they are there on the off-chance someone wanted some additional background or information. To be honest there's only about a dozen regular users but I still end up spending too long writing posts that seem more complete than they really needed to be. Brief questions, answers or thoughts with limited pause for grammar would actually do the job most of the time.
Anyway, I think you could well be right about Heaviside. Thanks for your time. There's a lot of history for Heaviside improving long distance communication and transmission lines - which is where the ideas would be important and first noticed.
Best Wishes.
Post by: paul cotter on 05/05/2022 06:45:18
Post by: Eternal Student on 21/05/2022 16:08:22
I'm sorry to add something to what was my own post but I've just found something that does seem relevant. I don't have anyone else to tell and it seemed so interesting that I've got to tell someone.
Does charge contribute to mass?
Yes, absolutely, no doubt, 100%, yes, yes it does. At least certainly in classical physics (including relativity - just not Quantum theories).
Relevant examples:
1. Capacitors have already been discussed. They really should have more inertia, more resistance to an applied force, when they are charged. Obviously the difference is small and there's no realistic hope of measuring it.
2. A more extreme example is obtained by the electron. Here the charge is significant compared to the mass and as you can imagine it now matters a whole lot whether you include the energy in the E field created by the electron as something that contributes to its mass.
The main result, in words, no equations: Classically, ALL of the mass of an electron is due to the energy in the E field. Let's say that another way - because it seemed interesting to me and can't be overstated:
Not only does the energy stored in the E field of an electron contribute to its mass, every scrap of the mass can be fully explained and accounted for as being due to the energy stored in the E field it creates.
Consequences: I fell off my chair.
Let's just be clear about a few things first: This isn't a new result in the world of physics, it's been known for a while. It's just well hidden. If you want to lower its importance, you can. You can argue straight away that this is ONLY a classical result; our best estimates are that electrons are actually best considered as genuine point particles..... there's stuff you could point at to suggest why the result isn't given much attention.
However, we're not going to do any of that. For the purposes of classical physics - the inertia or mass of an electron is significantly due to dragging around its E field when you apply a force to the thing you classically identify as being "the particle".
I'll skip all equations, I don't think anyone will want that.
References: It all hinges around "Compton Radius" as the radius of a uniformly charged spherical electron such that its rest mass is entirely due to the energy in the E field.
https://www.chemeurope.com/en/encyclopedia/Classical_electron_radius.html
Best Wishes.
Post by: paul cotter on 25/05/2022 12:16:56
Post by: Dimensional on 30/05/2022 05:57:03
Post by: Eternal Student on 31/05/2022 19:43:35
Sorry, it's taken me a while to notice the other replies.
where does the energy go when we bring two like charges together(ie the work done on bringing them together)?That's a very good question and there is some answer for that.
As you are aware (similar to the Hadrons having more mass than their component parts), when you bring two like charges together, force is required and would have been moved through a distance. So Energy was put into that system. That system should then have more mass than the individual particles when they were separated (infinitely far apart from each other). It does.
There are two standard ways of calculating this energy / mass change. To avoid this post getting too long, let's just have a look at one way.
Energy in the E field:
We have Energy density (Energy per unit volume) due to (or stored in, if you prefer) the E field at position x = ½ε |E(x)|2.
So the total energy in the E field = Volume Integral of that density where the position x varies over all of the space in the universe.
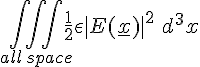
You mentioned that bringing the two like charges together distorted the E field. Well it does but it's a very simple effect. The E field obeys superposition principles. The E field from the two particles will be the sum of the E field produced by each one individually.
So the Energy in the E field due to particle 1 when it was infinitely separated from particle 2 is given by
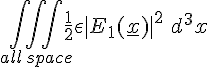
where E1 = the E field just from particle 1.
Similarly the Energy in the E field due to particle 2 when it was infinitely separated is
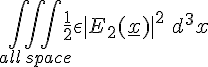
E2 = E field just from particle 2.
When you bring the two particles close together, the E field at a position x is precisely the sum of two separate fields.
E(x) = E1 (x) + E2 (x)
Note that this is a vector sum and we will want to determine | E (x) | and this won't quite be |E1| + |E2| unless the vectors are co-linear. However, they are almost completely co-linear through most of space when the particles are brought close together and would be precisely co-linear if the two particles had 0 distance between them. For simplicity we shall just have |E(x)| ≈ |E1(x)| + |E2(x)| but you are free to determine the exact calculation if you wish..
Anyway, the point is that |E(x)|2 is what appears in the expression for the energy density in the E field and the square of a sum is larger than the sum of the squares. (|E1| + |E2| )2 = |E1|2 + |E2|2 + 2.|E1| |E2|. So, now when we determine the total energy in the E field we obtain the following....
=
+ + 
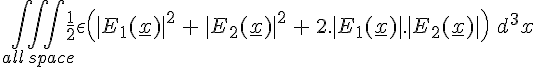
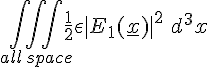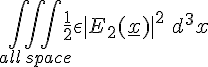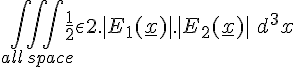
Where the first two integrals are precisely the sum of the energy stored in the E field when the two particles were separated. Meanwhile the third integral is a bonus - the extra energy that exists now that the particles have been forced together.
- - - - - - - -
So the work done in pushing the two charged particles together is seen in the E field. On a more practical level, you can actually measure it as an increase in mass that the entire system (the assembly of charged particles) has. It's exactly like the Hadrons you mentioned where the total mass of the hadron is greater than the sum of the separate masses of its constituent parts.
Best Wishes.
Post by: Armad on 02/06/2022 16:21:15
If a particle has a charge then it creates an electric field. If that energy is in the particle, then it would probably contribute to the total mass of the particle.
Hi , I was just browsing this forum and I found this question interesting . Suppose a particle has no electrical charge and does not emit an electric field . What if a particle just has field energy and charge was a product of interactions rather than something that exists as an entity ?
Particles could be viewed to absorb and conserve electrical energy that was created by interactions . In the electrodynamics of moving bodies , I have been working on a kinetic energy differential equation but note I still have some uncertainty .
kE=A
Kinetic energy is equal to area times the speed . I am not sure whether this helps you with this thread but I feel it is some how related .
Post by: Origin on 02/06/2022 18:01:41
What if a particle just has field energyWhat do you mean by field energy?
charge was a product of interactions rather than something that exists as an entityIf you are talking about particles, I don't believe that is a viable option. Electrons, positrons and protons always have the same charges, if the charge was due to an interaction of some sort then would occasionally see these particles with a different charge.
I have been working on a kinetic energy differential equation but note I still have some uncertainty .Area times speed does not give you energy. You would get the units of m^3/s. I don't know what that would be, but it certainly is not the units of energy.
kE=A Kinetic energy is equal to area times the speed .
Post by: alancalverd on 02/06/2022 18:17:30
1. Capacitors have already been discussed. They really should have more inertia, more resistance to an applied force, when they are charged.Hmm. "Charging" a capacitor means separating electrical charges within it, by applying an external voltage, or adding charge to one electrode and thus inducing an opposite charge in the other. Either procedure involves doing work and storing energy as stress in the dielectric. So there will be a mass increase associated with the stored potential energy, but not "charge" per se because the net charge remains zero!
Post by: Armad on 02/06/2022 18:59:57
What do you mean by field energy?
A bounded extension of a particle or particles in the form of light that is beyond the visible spectrum. The Earths magnetic field for example .
Post by: Origin on 02/06/2022 19:36:19
A bounded extension of a particle or particles in the form of light that is beyond the visible spectrum.This somewhat difficult since you are using nonstandard definitions for things. A field does not have anything to do with a form of light or any electromagnetic radiation. I would recommend you google "particle field definition" and see if that helps. I am sure if I try to describe a field it will only make it more confusing (probably confuse myself).
The Earths magnetic field for example .The earths magnetic field or any magnetic field is a good example of a field, as is the electric field. Neither one of these fields are a form of light or any type of EM radiation though.
Post by: Eternal Student on 02/06/2022 19:56:12
I am not sure whether this helps you with this thread but I feel it is some how related .Thank you. That is interesting.
I might just mention that I'm not trying to develop anything really "new". A lot of this is new to me - I haven't considered it before - but I'm not really trying to develop anything new to the world of physics.
Either procedure involves doing work and storing energy as stress in the dielectric.You're an engineer, Alancalverd and it shows. To be honest I had never considered physical stress as a store of energy for a capacitor but let's do that now: There would be some physical stress in the dielectric and you could measure the strain etc. However, a capacitor will work with just an air gap or even a vaccum between the plates (admittedly not as well but it will work). Not all of the energy stored in a capacitor can be explained as stress in a material.
"Charging" is what you call it. Yes, there is an equal opposite charge on the other plate but you can still call the process "charging up" that capacitor. However, it's fine if you want to call it separating some charge in the capacitor. That process results in the capacitor containing more energy and in principle therefore having more mass and more inertia, although the difference would be so slight I wouldn't try to measure it. It's not about the size of the change it's just that the change should be there.
Best Wishes.
Post by: Armad on 02/06/2022 21:07:42
I looked up the defintion that seems to be a little unclear , but to be honest I am not a parrot , who just repeats what is written on Google . All particles have a quantum field of some description , these fields without doubt have energy . These fields aren't emmited fields in my opinion and you are welcome to disagree . How do we know fields aren't bounded light that is beyond the level of present detection ?A bounded extension of a particle or particles in the form of light that is beyond the visible spectrum.This somewhat difficult since you are using nonstandard definitions for things. A field does not have anything to do with a form of light or any electromagnetic radiation. I would recommend you google "particle field definition" and see if that helps. I am sure if I try to describe a field it will only make it more confusing (probably confuse myself).The Earths magnetic field for example .The earths magnetic field or any magnetic field is a good example of a field, as is the electric field. Neither one of these fields are a form of light or any type of EM radiation though.
Fields will not naturally have frequency or a wave-length although I suspect that events can cause a field to wave. Atomic vibration being proportional to wave-length , the faster the hyper state , the shorter the wave-length .
Post by: alancalverd on 02/06/2022 22:16:20
However, a capacitor will work with just an air gap or even a vaccum between the plates (admittedly not as well but it will work).In the case of a vacuum capacitor there is a mechanical stress in the insulators that separate the plates. Vacuum has a dielectric constant, the permittivity of free space.
Quote
That process results in the capacitor containing more energy and in principle therefore having more mass and more inertiaMy point is that the energy stored in a capacitor is the potential energy resulting from the separation of charges. There is no additional charge resulting from "charging" a capacitor, so the mass change is not the mass of charge, but the energy-mass of charge separation.
Post by: Eternal Student on 03/06/2022 01:20:42
My point is that the energy stored in a capacitor is the potential energy resulting from the separation of charges. There is no additional charge resulting from "charging" a capacitor, so the mass change is not the mass of charge, but the energy-mass of charge separation.That sounds OK to me. I don't see that we have any disagreement. I might have phrased it differently and put the emphasis on the E field but that's all.
The separation of charge has resulted in a change in the Electric field. There is then a different amount of energy stored in that field. The capacitor is one of the text book examples* to illustrate that considering Energy stored in the E field gives exactly the same numerical answers as considering the energy required to separate those charges and create that final assembly of charges from the initial assembly of charges.
* For example, this reference was already given in the very first post: http://labman.phys.utk.edu/phys222core/modules/m6/field%20energy.html
and this quote was taken out of it: In electrostatics, viewing the energy as being stored in the separated charges or viewing it as being stored in the electric field leads to the same results. We are allowed to take either point of view.
The capacitor was a nice example to use because, for an ideal capacitor, the new E field you get from the separation of charges is contained or restricted to the region of space between the plates, while the E field outside of that region is completely unaffected. So there's not much problem or concern about saying where that energy is located... it's in the capacitor for sure. There's just a choice of thinking about it as potential energy that is in the charges or else as energy that is in the E field.
Best Wishes.
Post by: paul cotter on 03/06/2022 10:02:22
Post by: Kryptid on 03/06/2022 20:14:24
kE=A Kinetic energy is equal to area times the speed .
That equation doesn't work. Kinetic energy is proportional to mass.