Post by: Kryptid on 20/06/2022 03:06:27
In accordance with general relativity, the space near a massive body isn't perfectly Euclidean. Does this mean that the inverse square law is only an idealized approximation and might fail to produce accurate calculations under certain circumstances, such as those close to black holes?
Post by: Halc on 20/06/2022 03:57:30
It falls apart at extremes. For instance near a black hole, the inverse square law has your weight (force required to maintain a constant altitude) approaching some finite quantity, where in reality, at the EH, no force is enough to do that.
It also falls apart for great distance since spacetime isn't Minkowskian at the largest scales. There cannot be a global inertial frame, and the inverse square law I think is a property of an inertial frame.
Post by: Kryptid on 20/06/2022 04:45:37
It also falls apart for great distance since spacetime isn't Minkowskian at the largest scales.
Any idea what distances such a thing would happen at?
Post by: Halc on 20/06/2022 06:14:01
Any idea what distances such a thing would happen at?It's kind of like asking when normal velocity addition stops working and when relativistic addition must be used. It depends on the precision you want, but right away if you want infinite precision.
For the small scale (the black hole example), we talk about 'local' tests, that say there isn't one to distinguish acceleration from gravity. So the answer to the question is the distance needed to distinguish the two cases, which of course depends of the precision of your instruments.
On the large scale, I would say 'far enough that dark energy is measurable'. That means I have two small pebbles held apart at distance X by a rigid rod, far away from gravity sources. Now you let go of the pebbles. In inertial space, they'll stay put per Newton's first law. But dark energy will accelerate them apart (and normal space expansion will not). If you can measure that, the inverse square law is also probably measurably off. Dark energy messes up all the formulas, and is the primary reason inertial frames (and their rules) cannot be global.
Post by: evan_au on 20/06/2022 09:13:54
- If you move twice as far away to distance 2d, the intensity drops by a factor of 4.
As a side-note:
However, you can get relativistic beaming in scenarios such as:
- sources are traveling close to c (Special Relativity)
- sources are close to a black hole (General Relativity)
This affects the distribution of intensity (no longer isotropic), the total intensity of the source (due to time dilation) and its wavelength (the relativistic Doppler/Einstein shift).
- In the case of a source close to a black hole, some of the radiation is swallowed, never to reappear, so the total intensity is reduced.
https://en.wikipedia.org/wiki/Relativistic_beaming
Since merging black holes often travel at a fair fraction of c, similar beaming of gravitons would occur (but much harder to detect than with light!)
Post by: Eternal Student on 21/06/2022 00:47:43
Before adding anything to this thread it would be useful to know if @Kryptid is already done or satisfied with the replies.
Best Wishes.
Post by: Kryptid on 21/06/2022 00:50:50
Hi.
Before adding anything to this thread it would be useful to know if @Kryptid is already done or satisfied with the replies.
Best Wishes.
I'm satisfied, but it's perfectly fine if you have something to add.
Post by: Eternal Student on 21/06/2022 12:03:12
Let's do this in small chunks with time for tea break in between posts. First we'll consider the basic inverse square law and one way we can violate it in curved space that has a real-life example (a black hole) we can point to.
Well the inverse square law usually arises when you have a source that emits particles equally in all directions.
You can specify the details more precisely OR allow some randomness (for example have particles emitted with random velocities but no preference for the direction of those velocities) - the most important thing is that the emissions are isotropic (much the same in every direction from the source). The other assumption is the particles travel away from the source in straight lines (for example that's what photons or rays of light would do).
Here's a quick diagram of the situation:
emissions-isotropic.png (7.16 kB . 503x400 - viewed 3741 times)It's important to remember that this should be a 3-Dimensional thing but the diagram is just a 2-D slice as usual, particles are being thrown out by the source in all directions.
Now imagine drawing a sphere centred on the source with a radius r.
emissions-sphere.png (10.47 kB . 551x452 - viewed 3774 times)The general reasoning is that the emitted particles must pass through the surface of that green sphere on their way further out into space. We're going to assume you're familiar with this idea and just speed through it:
If the source emitted N particles in total every second, then N particles must pass through the sphere every second. The sphere has a surface area of 4πr2, so the flux of particles through the spherical surface is N / (4πr2). That might also be called the bombardment intensity and it is the number of particles hitting the surface (or crossing through) per unit area of the surface and per second. Since the emissions were isotropic the flux is the same over any patch anywhere on that sphere. If we remove the spherical surface and just put a small piece of flat surface with an Area A (keep it small so we can say that all of it was a distance r from the source) at distance r from the source, then the bombardment intensity for that little flat surface is also given by N / (4πr2).
We see that the intensity (or flux across a surface) falls off as 1/r2. We have the inverse-square law.
Let's put a particle detector at a distance r from the source, with everything in standard flat space. It gets it's usual fair share of particles bombarding it. In my sketch it looks like 1 particle track is passing through the detector.
emission-flat.png (11.46 kB . 541x561 - viewed 3766 times)Now let's do the same in curved spacetime. Here we have a black hole on the left hand side. The main difference is that the particles don't take a straight line path after leaving the source in this situation. Those particles are following a geodesic and spacetime curvature makes that a curved trajectory. I'm taking a lot of liberties in this sketch but I've tried to show that in this configuration the detector is getting more than its fair share of particles pass through it. About 3 particle tracks are passing through the detector.
emission-cuved.png (16.12 kB . 906x691 - viewed 3838 times)If we picked up the particle detector and put it on the right hand side of the source then less than the usual amount of particles pass through the detector. Overall the 1/r2 law for the intensity has been lost because the intensity depends on the exact location of the particle detector and not just on it's scalar distance from the source.
As I said, I was taking lots of liberties there.... the diagram illustrates the point but without any fine details. The metric is the Schwarzschild metric but the diagram is drawn on a flat screen in Euclidean space. So we need some agreement about what is being shown and how. I've tried to keep the black hole in a line with the detector and source because then the area of the detector (its height up the page and depth into the page) is determined by changes in the angular co-ordinates from the black hole and so this would look much the same even if you picked it up and put it on the right hand side of the source. However the distance from the source wouldn't quite look the same, when the detector is close the black hole, the radial co-ordinate R from the black hole has a high value for distance determination (1 unit change in R is worth a lot of distance when you're close to the black hole). So on our diagram putting the detector over on the right hand side but at the same metric distance could look like the detector was actually a bit closer to the source - this all depends on what we decide the x-axis or horizontal axis along the page is showing. The details for the diagram aren't too important - it's just illustrating the concept.
Best Wishes.
Post by: paul cotter on 21/06/2022 14:48:47
Post by: Eternal Student on 21/06/2022 18:09:57
So the inverse square law can be violated if the emitted particles don't take straight line paths, that was discussed in the earlier post. As it happens most of that was caused by curvature in the time component of spacetime rather than because just the space part was non-Euclidean. Your ( @Kryptid ) original question seemed to want more attention on just space being non-Euclidean.
We can do that, however, in real-life or real-universe situations we don't often get a lot of curvature in the purely spatial part of spacetime. So, for one thing there's no good examples that provide a lot of intuition. Also, it's inevitable that if we put a little curvature into the spatial part, i.e. make space obviously non-Euclidean, then we actually end up twisting Spacetime to (searching for a suitable expletive) well.... a lot. What that means is that it can be very hard to identify what time is doing or that it behaves in any way like the time we imagine. So you'd end up going home and quite uncertain if time had been messed with or if it really was just the space part.
So, we're going to try and build an example where time is handled as easily as possible.
This is the usual metric for flat Minkowski space, written with spherical co-ordinates:
ds2 = [ dr2 + r2dθ2 + r2Sin2θ dφ2 ] - c2dt2
I'm assuming you (Kryptid) have seen something like this before and I'll just rush through the principles in case someone else is reading the post.
We're using spherical co-ordinates (r, θ, φ) as shown in this diagram:
(https://upload.wikimedia.org/wikipedia/commons/thumb/4/4f/3D_Spherical.svg/360px-3D_Spherical.svg.png)
The bit in [Square brackets] is the metric on the spatial part and that's all we'll really need to focus on. The metric just tells us about the size of (the square of) the distance moved when we change the radial co-ordinate by a small amount dr and the angles by a small amount dθ and dφ respectively. Many texts will describe this in more detail if it's required.
We're just going to change that metric slightly:
ds2 = [ dr2 + r2dθ2 + (1). Sin2θ dφ2 ] - c2dt2
We've not adjusted the time part at all. We've just removed a coefficient r2 from the front of the dφ contribution and replaced it with 1 written in red so you'll notice it. That small adjustment is sufficient to make our space quite weird and certainly not Euclidean.
What it's saying is that no matter how far away from the origin you are, a small change in the azimuthal angle is worth the same amount of distance. Meanwhile, distance changes conventionally with changes in the polar angle - if you are at a large radial distance r from the origin then changing the polar angle will result in sweeping out a large distance through space.
Here's a diagram:
NonEuclidean.png (8.33 kB . 613x441 - viewed 3722 times)If we take a section so that the y-axis is what runs up the page on that diagram, then everything behaves as you expect. The two red arcs have different lengths, the one further out is longer as usual. However if you take a section through space so that the z-axis is what runs up the page then things are strange. Distances along the radial blue lines still behave normally but the red circular arcs will actually have exactly the same lengths in our metric.
OK, I hope you have the idea. This space is a bit weird and there's no way to show what it "looks like" in a diagram because we are and the computer screen is, in flat space.
In some small regions of our non-Euclidean space, it actually is just ordinary Euclidean space. In all regions where r ≈1 the space is locally flat and perfectly normal, everything makes good common sense. As you move away from r ≈1 the space takes on progressive curvature and Euclidean geometry fails to apply.
Now let's have our point source emitting particles, we'll put it at the origin and we'll surround it with a surface at constant radial co-ordinate r as usual:
emissions-sphere.png (10.47 kB . 551x452 - viewed 3719 times)This post is getting a bit long so we'll speed up....
Make all the usual assumptions.... particles must pass through the surface at constant r on their way further out into space... etc.... (Minor note, I've tried to be careful with the metric, the emitted particles should follow straight line radial paths after leaving the source WHEN the source is at the origin, geodesic paths can get weird if the source is elsewhere).
The main thing is that this surface doesn't actually have a surface area of 4πr2 any longer. The space is so curved that a surface at constant radial co-ordinate, r (which we world ordinarily call a sphere of radius r), has a surface area given by 4πr and not 4πr2.
An area element, dA, for the surface is shown in this diagram:
Area element.png (6.54 kB . 613x441 - viewed 3707 times)Note that the lengths along the sides of the area element are determined by using the non-Euclidean metric. For the length in the direction of increasing θ (written on the left in the diagram), we hold r and φ constant and allow only θ to vary. We have ds2 = [ dr2 + r2dθ2 + (1). Sin2θ dφ2 ] (you can subtract a 0 time change if you want to use the spacetime metric and not just the metric on space, we're intersted in the distances in space which are the spacetime intervals you see when you take a slice through spacetime at constant time).
We end up with, dS2 = 0 + r2dθ2 + 0 - 0 = r2dθ2 and hence, dS = r dθ as shown on the diagram. Do the same sort of thing to get the length in the direction of increasing φ. Overall then, dA = r Sin(θ) dθ dφ.
If you just don't care, then that's fine.... that's how you would have thought an area was found, we're done, move on. However there might be a few that know defining an area in non-Euclidean space isn't simple and want to check a few details. I was careful to set up a metric so that the vectors
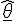and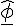 
are orthogonal w.r.t. the given metric and we can define an area as shown. There'll be a bit more discussion about area later.To find the total area of the surface we have to integrate as usual:
= 
= 
=
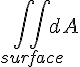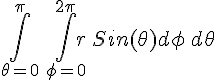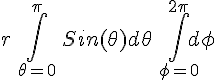
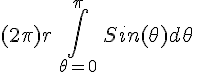= 4π rOK, so the emitted particles are passing through that sphere but the sphere only has a surface area of 4π r in this curved space, which means the average flux or bombardment intensity on the sphere's surface is N / (4πr) in this space. We obtain a 1/r law for intensity and not a 1/r2 law.
If you don't have the source at the origin then the particles can follow more unusual paths and we would have a situation similar to that shown in an earlier post (with the black hole) where the intensity can be higher in one direction from the source instead of from another direction - that only makes the 1/r2 even less valid.
This post is already too long... I think I was going to briefly discuss some complications with areas but...well... I'm just not going to do that.
Best Wishes.
Post by: paul cotter on 21/06/2022 18:34:27
Post by: Eternal Student on 21/06/2022 18:46:50
I see a dimensional conflict...Yes. I almost mentioned this in the post but it was already too long - because all good scientists are trained to check the units and dimensions.
The metric has a form where φ actually has dimesnions of length:
ds2 = (stuff with an overal dimension of length2) + Sin2(θ) dφ2.
We'll leave the θ as a dimensionless angle, then the dφ2 must have dimensions of length2.
Anyway, In the final expression for the surface area 4πr, that is really 2 . (2π) . r where the (2π) has dimensions of length.
Best Wishes.
LATE EDITING: Having a dimension assigned to what looks like an angle can seem very hard to swallow. If it helps, the space can be considered and conceptualised as something with flat (2-D) polar co-ordinates (r, θ) and a third dimension φ which is the depth into the page. The depth into the page just happens to permit a range between 0 and 2π. That helps to see φ as something that can have dimensions of length. As I mentioned, there's no good way to visualise this very non-Euclidean space and re-drawing everything with that sort of representation just strains understanding elsewhere.
Post by: Eternal Student on 21/06/2022 20:35:23
The inverse square law (whether related to gravitational field strength....We've had a bit of discussion about the inverse square law as it might apply to various things like e-m radiation or particles emitted by some point source. I've avoided considering gravity itself and the inverse square law for gravitational force. So let's do that now, it's a bit shorter than some of the other posts:
The inverse square law describing the gravitational field strength is evidently shot to pieces.... Mainly because the field strength is the force per unit mass and that has the word force in it.
The moment you've got extreme or rapidly changing spacetime curvature we can't even consider gravity as a force.
Best Wishes.
Post by: Eternal Student on 24/06/2022 18:41:11
It's just too quiet today. So I'm going to pick a minor thing that was said earlier, which I'm not entirely certain of.
It also falls apart for great distance since spacetime isn't Minkowskian at the largest scales. There cannot be a global inertial frame, and the inverse square law I think is a property of an inertial frame.@Halc usually doesn't mind if their comments get questioned.
The agreement:
I think the inverse square law fails in an expanding universe.
But...
the disagreement:
Not for the reasons outlined.
Firstly, I'm not too concerned about the inverse square law for gravity. That ship has sailed - there's loads of reasons why Newton's laws of gravity don't adequately explain some situations and the expansion of space is one of those. As it happens, you can build something very similar to the Friedmann equations describing the apparent expansion of the universe using just Newtonian laws. However, a lot more can be explained by assuming it is the fabric of space itself that is expanding (and hence GR as a model of gravity) rather than the movement of objects (like planets) through space (Newtonian motion and gravity).
(Reference: On a really quite day, when you have a spare 4 hours, there's a series of lectures from Leonard Susskind of Stanford University that are freely available on You Tube and they do exactly this - build the Firedmann equations from Newton. Otherwise, you may be willing to just take my word on it)
So what we're left with is the inverse square law for most other things, such as the intensity of e-m radiation from a (point) source.
The agreement:
The expansion of space causes e-m radiation to be red-shifted, wavelengths increase as light travels through expanding space. For that reason, the inverse square law for intensity would not hold. The intensity of e-m radiation received at a distance r would fall off faster then 1/r2 (~ r - n with n>2 but that index n might depend on the behaviour of the scale factor a(t) for the universe, so the exact value might vary as the universe evolves). The comment about the lack of a global inertial reference frame is also spot on correct in this situation. The wavelength changes because you just can't measure the wavelength in the same frame as where it was produced even if you wanted to.
The disagreement:
Suppose it wasn't e-m radiation that was being emitted by the point source. Suppose it was something else like Beta particles being emitted isotropically by the source. Why would that not follow the 1/r2 law for the bombardment intensity received on the surface of a sphere held at a constant metric distance (a radius) r from the source?
I don't know, I haven't done the calculations or thought about it much - that's why I'm asking.
First thoughts are as follows:
(i) Keep it simple and assume the Beta particles have the same initial speeds, just various different directions of emission from the source. The expansion of space should start to reduce those speeds. This tends to reduce the number of Beta particles that will pass through the spherical surface in 1 unit of time.
(ii) Working against the idea in (i), space itself is expanding and therefore some space and everything in that space (even if it had 0 velocity) is passing across the surface of the sphere in 1 unit of time. Equivalently, because we insisted that the sphere retains constant metric distance from the source and isn't co-moving, we are dragging it like a fishing net through space to achieve that.
(iii) The basic idea of "intensity" needs to be examined. It's an amount of energy per unit area but also PER UNIT TIME. What time would you use? The Co-moving or co-ordinate time seems reasonable but you might use the time that passes for an observer always located on the surface of the sphere at the place where the intensity was being measured. We insisted on keeping that sphere at a constant metric radius from the source, so that observer is not co-moving with the universe and therefore their proper time intervals are not given by the changes in co-ordinate time.
Anyway.... seems complicated and uncertain. I think we can reasonably assume the inverse square law won't hold for e-m radiation but I really don't know if it holds for the emissions of some other types of things.
Best Wishes.
Post by: evan_au on 24/06/2022 22:52:52
Quote from: Eternal Student
Suppose it was something else like Beta particles being emitted isotropically by the source.If we assume that the particles are traveling at (say) c/10, then there will be an event horizon beyond which these particles will not pass, because space will be expanding faster than c/10 by the time they got there.
- This event horizon will be much smaller than the event horizon for light (which defines the limits of our observable universe).
Post by: Eternal Student on 24/06/2022 23:38:14
I do like the reasoning @evan_au, however I don't think it holds (sorry).
The reasoning about Event Horizons is almost backward. Even if the Beta particles had almost 0 velocity, or do drop to exactly 0 velocity soon after emission, over enough time the space between the beta particles and source will expand. So, given enough time the distance between Beta particle and source > fixed radius r. That will put the Beta particle outside the surface where the intensity is being measured.
None the less, if the expansion of space is very unusual, so that it is actually negative (or to phrase that another way so that space actually contracts instead of expanding) then something like your idea will hold. There is an event horizon at a fixed physical distance, r, such that Beta particles emitted by the source can never cross that EH. Then the 1/r2 law for intensity evidently fails, the intensity drops to precisely 0 for r ≥ that horizon radius.
Best Wishes.
LATE EDITING:
assume that the particles are traveling at (say) c/10, then there will be an event horizon beyond which these particles will not pass, because space will be expanding faster than c/10 by the time they got there.The main issue is that the velocity of the Beta particles isn't an absolute or frame independant thing. By the time they reach your EH they are travelling at far more than c/10 relative to the source. The speed c/10 is their speed through every local patch of space they find themselves in.
Post by: evan_au on 25/06/2022 10:08:47
Quote from: Eternal STudent
The reasoning about Event Horizons is almost backward.I was not thinking about a horizon at a fixed distance.
- After all, the size of our observable universe is not at a fixed distance - it expands at the speed of c.
- But space can expand faster than c, so (in principle) there are distant galaxies that people on Earth could see today, but
which will not be visible in 10 billion years, because the expansion of space has carried them outside our visible universe.
- If you posit some particle that travelled at c/10 (and didn't slow down), there would be regions of our visible universe that could never detect these particles, because the space in between is/will be expanding faster than c/10.
Usual disclaimer: Ignoring intergalactic medium, electrostatic forces, magnetic fields, etc which will change the velocity and/or direction of real beta particles.
Post by: Eternal Student on 25/06/2022 14:33:45
I'm always very grateful for anyones time spent in conversation. So thank you very much @evan_au.
However, I can't always agree with everything and that is the nature of discussion after all. What you've said isn't wrong, it's just misleading. Although, equally, what I've said before could be considered misleading.
We need to establish a few things and then hopefully we will be seeing and understanding the same things.
I was not thinking about a horizon at a fixed distance.OK - BUT you should be. The inverse square law is about the intensity received at a distance, r, from the source. That is a physical distance, so it is determined by the metric. It is not determined by reference to a difference in the values assigned to locations in the co-ordinate system we commonly use to describe an expanding universe.
The usual co-ordinates used in an expanding universe are the called the co-moving co-ordinates. Galaxy 1 can have fixed co-moving co-ordinates and it's tempting to say it has a fixed position. Galaxy 2 can also have fixed co-ordinates and we can be tempted to say it has a fixed position. The co-ordinate differences between the galaxies never changes, so that seems fine. However, the physical distance between the galaxies is increasing with time, in that respect it doesn't look like the galaxies are fixed in position in any ordinary sense of the word. To avoid the confusion, it's best if you just don't say or imagine that either of the galaxies have a fixed position. Instead, just say that the galaxies are "co-moving with the universe", or that they are "co-moving" for short.
But space can expand faster than c, so (in principle) there are distant galaxies that people on Earth could see today, butThis is correct. However, the light emitted by the distant galaxy will travel an infinite physical distance. It's just that how far it can go in 1 unit of time will not be sufficient to match the expansion of space that is occurring between the distant galaxy and earth.
which will not be visible in 10 billion years, because the expansion of space has carried them outside our visible universe.
We would place our sphere, where the intensity is being determined, at a fixed physical distance from the distant galaxy and not at a fixed co-moving co-ordinate separation from the distant galaxy. The light from that distant galaxy will reach the surface of that sphere. Just to get the image and understanding right, the surface of that sphere might have started at time t=0 precisely where planet earth was. However, the surface of that sphere will be a long way from earth at a later time t=1 unit, when the photons from the distant galaxy finally cross over that sphere.
We can place a sphere with a fixed physical radius, r, around the distant galaxy (it doesn't matter how large r is) the photons from that galaxy will (eventually) reach the surface of that sphere. In no way does this contradict the idea that the photon won't reach earth - the surface of the sphere is nowhere near planet earth when the photons cross over the sphere.
If you posit some particle that travelled at c/10 (and didn't slow down), there would be regions of our visible universe that could never detect these particles, because the space in between is/will be expanding faster than c/10.Yes, total agreement. However, that has nothing to do with the particles crossing over a sphere at some fixed and pre-determined physical distance from the source.
Best Wishes.
Post by: Halc on 26/06/2022 02:58:44
Suppose it was something else like Beta particles being emitted isotropically by the source. Why would that not follow the 1/r2 law for the bombardment intensity received on the surface of a sphere held at a constant metric distance (a radius) r from the source?Presuming you didn't do anything funny like put detector/source at different potentials, the inverse square law would work given this constant r (say both held at opposite ends of a stick). Space expansion would make no difference. Dark energy probably would, but that counts as 'something funny' just like gravity does. Dark energy would put tension on the stick. Space expansion would not.
If we assume that the particles are traveling at (say) c/10, then there will be an event horizon beyond which these particles will not pass, because space will be expanding faster than c/10 by the time they got there.OK, but if distant detector is held at constant distance from this emitter, it will cross over that 'event horizon' (towards us) and the particles will get to it.
What you're talking about isn't the event horizon, it's the Hubble radius, the distance where Hubble's law yields c. The event horizon is a little further away from that, and it has to do with acceleration, and is not a function of the current expansion rate like the Hubble radius is. So a beta particle moving at 0.1c would get at most a 10th of the way to the Hubble radius, and would take an infinite time to do so.
Quote
This event horizon will be much smaller than the event horizon for light (which defines the limits of our observable universe).The light event horizon is about 16 BLY away. Current radius of the visible universe is about thrice that, so they're very different things. The latter is all the material in the universe which at some past time might have had a causal impact on a given event (Earth, here, now). The event horizon is the comoving distance of the nearest current event from which light can never reach here in any amount of time.
After all, the size of our observable universe is not at a fixed distance - it expands at the speed of c.The Hubble sphere expands at c (by definition). The visible universe expands at somewhat over 3c, which is why we can see galaxies that are currently about 32 BLY away (comoving distance). The event horizon is barely expanding at all.
Quote
so (in principle) there are distant galaxies that people on Earth could see today, butHate to disagree, but new galaxies become visible over time. The most distant ones were not visible several billion years ago, even if one used the best telescopes. Yes, the galaxies cross beyond the event horizon, but that doesn't mean we can't see them any more than we stop seeing somebody falling into a black hole.
which will not be visible in 10 billion years
The inverse square law is about the intensity received at a distance, r, from the source. That is a physical distance, so it is determined by the metric. It is not determined by reference to a difference in the values assigned to locations in the co-ordinate system we commonly use to describe an expanding universe.Just so, yes.
Quote
The usual co-ordinates used in an expanding universe are the called the co-moving co-ordinates. Galaxy 1 can have fixed co-moving co-ordinates and it's tempting to say it has a fixed position. Galaxy 2 can also have fixed co-ordinates and we can be tempted to say it has a fixed position.Right. The rate that a given galaxy changes its coordinates is called peculiar velocity, and the peculiar velocity of almost all objects is quite low, a few percent of c at best.
Quote from: evan_au
If you posit some particle that travelled at c/10 (and didn't slow down)In an expanding metric, the paricle will slow down without some force maintaining its peculiar velocity. Newton's laws only work in a static metric.