Naked Science Forum

On the Lighter Side => New Theories => Topic started by: talanum1 on 23/09/2022 13:21:45

Title: Is There a Problem With Cantor's Diagonal Proof?
Post by: talanum1 on 23/09/2022 13:21:45

Yes. He does not write down the extra number to the infinite'th digit. To remedy this one has to write down the list together with the n'th digit:

 1 2 3 4 ... n n+1
.2 3 4 5 ... 6 7
.3 4 5 6 ... 7 8
...
....             9 1

and then specify that when you write down the extra number to (if you change the n'th digit by one) to also change the n+1'th digit by one. Then, by induction you can claim to have written down the number not on the list.

Title: Re: Is There a Problem With Cantor's Diagonal Proof?
Post by: talanum1 on 23/09/2022 14:09:13

There's just one problem with this: because n can change, you do not know the digit under the n'th index so you can't change the n'th or (n+1)'th digit. To remedy this we must write down the list as follows:

 1 2 3 4 ... n (n+1)
.1 2 3 4 ... p a
.2 3 4 5 ...
....
.v w x ...   c
.q r s t ...  u b

and write down the number not on the list as:

.2 4     ... c+1 b+1

Then the reasoning would be: since at least one digit in the list must be unique at it's place, the number written down is indeed a number not on the list - he leaves out this reasoning.

Title: Re: Is There a Problem With Cantor's Diagonal Proof?
Post by: talanum1 on 23/09/2022 14:46:46

Just one problem with this: it supposes there is a largest number (n+1), and there isn't.

So we cannot write down a number not on the list. So does it exist even if we cant write it down? Root 2 is writable as .

Title: Re: Is There a Problem With Cantor's Diagonal Proof?
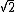Post by: Colin2B on 23/09/2022 15:03:47

Quote from: talanum1 on 23/09/2022 14:46:46

Root 2 is writable as .

The largest number can be written as (n+1). So?

Title: Re: Is There a Problem With Cantor's Diagonal Proof?
Post by: talanum1 on 23/09/2022 15:06:44

We can write down the number: call the list L and the operation of adding 1 to the digits as O_n. Then the number not on the list is:

lim_{n -> ∞} O_n(L).

Title: Re: Is There a Problem With Cantor's Diagonal Proof?
Post by: talanum1 on 23/09/2022 15:10:46

Point is: writing the largest number as (n+1) is wrong: there is no largest number, otherwise we can construct n+2 etc.

Title: Re: Is There a Problem With Cantor's Diagonal Proof?
Post by: Colin2B on 23/09/2022 17:24:26

Quote from: talanum1 on 23/09/2022 15:10:46

Point is: writing the largest number as (n+1) is wrong: there is no largest number, otherwise we can construct n+2 etc.

No, you just say n+2 is the new n+1 and the old n+1 is now n
Don’t understand your problem,

Title: Re: Is There a Problem With Cantor's Diagonal Proof?
Post by: talanum1 on 24/09/2022 09:53:48

You can't claim n + 1 = n + 2. This is not computer science. This just confirms the fact that there is no largest number.

Technically we cannot write down ∞, we may just write lim_{n-> ∞} n. Or write ∞ as shorthand for this.

Title: Re: Is There a Problem With Cantor's Diagonal Proof?
Post by: Colin2B on 24/09/2022 10:05:23

Quote from: talanum1 on 24/09/2022 09:53:48

You can't claim n + 1 = n + 2. This is not computer science.

I’m not claiming that. I’m saying you transpose n+2 becomes the new n+1

Title: Re: Is There a Problem With Cantor's Diagonal Proof?
Post by: talanum1 on 24/09/2022 10:14:11

You can do such a operation in mind or on computer, but it is not mathematically correct.

Your saying n+2 = O(n+1). I'm saying then O(n+1) = n+1+1 > n+1

Title: Re: Is There a Problem With Cantor's Diagonal Proof?
Post by: Colin2B on 24/09/2022 13:43:39

Quote from: talanum1 on 24/09/2022 10:14:11

Your saying n+2 = O(n+1).

no I’m not

Title: Re: Is There a Problem With Cantor's Diagonal Proof?
Post by: talanum1 on 07/10/2022 17:49:20

The prevailing thought is that you can reach an infinite amount of time. This is false: 13.7 billion years from now infinite time would be just as far away as it is today.

Title: Re: Is There a Problem With Cantor's Diagonal Proof?
Post by: pzkpfw on 07/10/2022 20:09:58

That's not an issue in math.

I can write in moments the symbol ∞ to represent all of infinity.

I can write 0.9... = 1; where the "..." represents infinite 9 digits, not having to worry that I'd never be able to write them all down, even in infinite time.