Post by: Eternal Student on 22/11/2022 03:50:42
Anyone know of a good explanation / derivation of the free vortex velocity formula?
V(r) = k/r ; with V(r) = velocity of the fluid at radius r (and it will be tangential); k = constant ; r = radial co-ordinate.
Just to formalise, using cylindrical co-ordinates (r, θ, z) a free vortex around the z-axis can be defined to be a fluid flow where the velocity field is given by:

(https://upload.wikimedia.org/wikipedia/commons/c/c0/Vorticity_Figure_02_a-m.gif) Animated image from Wikimedia.
That's all some texts do, just define it that way. However some try and go a bit further and explain why this sort of velocity field would be reasonable from some elementary assumptions about what is happening. What I'd like to see is a good derivation of that formula.
I've been Googling the thing for a while now and not found much that is reliable.
This post is already long and the main thing is for me to ask you something - I would like a good derivation from some elementary assumptions. I'll put one weak argument under a spoiler, you can see it if you want. The post is not about me telling you stuff. It's just that if you do find a derivation based on angular momentum, pause for a moment and see if it really is reasonable. I'm always happy for any discussion.
Spoiler: show
Best Wishes.
Post by: alancalverd on 22/11/2022 17:47:40
Post by: Eternal Student on 23/11/2022 05:15:20
That's an outstanding answer and you can have the "best answer" award for that. It's taken me a while to think about and I'm just astounded by your ability to put something into a few words. Thank you very much.
I don't have the ability to compress something into a handfull of words but I think you were saying something like this (which I'll put under a spoiler because it would be better to keep the post short and any other comments coming in).
Spoiler: show
Best Wishes.
LATE EDITING: Made some adjustments, it'll do.
Post by: alancalverd on 23/11/2022 11:44:04
As for the constant of integration, clearly as r → ∞, V → 0, so surely c = 0? Or is the entire universe rotating under some mysterious ∑ c > 0 thanks to an unpaired butterfly in orbit somewhere? ;)
*Big bum, short of breath - that's me!
Post by: Eternal Student on 23/11/2022 14:25:33
I agree the constant c should be 0 for a vortex extending to infinity (which is the simplest idealistic version of a free vortex flow). Well spotted.
I was thinking it could be negative for a free vortex (an approximate free vortex) contained in some finite region like a big cylinder (or a big flooded road). That's then interesting because we can have some inner region with a clockwise flow, a quiet patch and a counter-clockwise flow further out. I think I've seen effects like this in a You Tube video with flooded roads that had leaves and debris on the surface to trace streamlines naturally. It's not that this sort of odd motion will usually be established when you start up a vortex and all the water was calm and static to begin, that's not what I think would happen. It's just that if the outer part of a large body had some rotation clockwise to begin with, then this can continue for a long time much as a steady flow solution while someone unblocks a drain cover and starts up a counter-clockwise vortex near the centre of that body of water. Provided the velocity profile settles down to v(r) = (k/r) - c then this should be a viable un-forced steady flow solution for a fluid with a small viscosity.
Velocity profiles of the form v(r) = (k/r) + c with c positive are never likely to be sustained just because the fluid has more kinetic energy in that solution than with c=0. Viscous forces tend to reduce the kinetic energy and dissipate heat. However, for a negative value of c, I think you could get the clockwise and counter-clockwise motion described and in a container of the right size that doesn't need to be a higher total kinetic energy.
Hmmm.... Wish I could find the YT video of someone unblocking a road drain with exactly the sort of outer counter-clockwise and inner clockwise rotations being sustained for a very long time.... can't find it now.
Best Wishes.
Post by: alancalverd on 23/11/2022 15:39:36
V will have to decrease faster than 1/r because the fluid in contact with the pipe isn't moving, so you need to invert your analysis, beginning with the stationary boundary layer and allowing V to increase towards the centre.
Fortunately the classical models for viscous laminar flow in a pipe will give you the answer, with the mass flow now being in the plane of the page instead of across or out of it.
Once you introduce opposing vortices you are moving towards turbulent flow characteristics at the boundary between them, and as soon as you introduce nonzero viscosity and velocities at the boundary, the system necessarily becomes unstable.
Post by: Eternal Student on 23/11/2022 21:07:55
The old pedant says you can't have a free vortex if it's contained!There seems to be several different definitions of "free" used to describe a "free vortex flow" that I can find from different websites and sources. *
1. It's not driven.
2. It's not contained and not driven.
3. The velocity of the fluid is given by v = (k/r) and tangential. Make of it what you will.
* Shipping costs, tax and handling fees obviously still apply. You can't avoid that.
Definition 3 seems to be favoured (as mentioned in an earlier post) and you could obviously argue there were no limits imposed on r.
V will have to decrease faster than 1/r because the fluid in contact with the pipe isn't moving...Set c = -(k/R) where the pipe has radius R. Then a flow given by v(r) = (k/r) + c (and in the
 direction) satisfies the boundary condition v(R) = 0. I'm not sure if you'd still call that a free vortex flow but it has most of what you'd want. E.g. the velocity still falls off only as 1/r, it's curl free (irrotational) everywhere except at the origin.
direction) satisfies the boundary condition v(R) = 0. I'm not sure if you'd still call that a free vortex flow but it has most of what you'd want. E.g. the velocity still falls off only as 1/r, it's curl free (irrotational) everywhere except at the origin. On the other hand, it doesn't really offer any automatic conservation of angular momentum for a particle that wanders from an outer track to an inner track like the profile v = (k/r) would and it just doesn't have the profile v(r) = (k/r) if you were taking that as a definition of a free vortex flow. The lack of an automatic conservation of momentum probably makes the flow less stable, in real life as particles do sometimes wander from one radius to another they need torque which they must be obtaining from other parts of the fluid if the vortex is not driven.
I'm just about done with Fluid dynamics for a few days, I'm ready to put the book back on the shelf. I'm happy there's at least a few reasons why the velocity k/r is reasonable for a free vortex instead of just accepting the definition of free vortex flow as being one with that velocity field. Thanks again for your time.
Best Wishes.
Post by: paul cotter on 23/11/2022 21:31:54
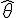 direction). We can argue that v = v(r) = function of r only because of the symmetry of the situation and that the entire velocity is (mainly) tangential from an earlier assumption.
direction). We can argue that v = v(r) = function of r only because of the symmetry of the situation and that the entire velocity is (mainly) tangential from an earlier assumption.
 = velocity of the fluid orthogonal to the r direction and hence actually in the plane, A = Area of the plane, r = direction orthogonal to the plane, directional derivative shown with grad operator if you prefer it).
= velocity of the fluid orthogonal to the r direction and hence actually in the plane, A = Area of the plane, r = direction orthogonal to the plane, directional derivative shown with grad operator if you prefer it).  =
= 
 .
.
 on a section of the ring at radius r and with angle between θ and θ+dθ. Hence,
on a section of the ring at radius r and with angle between θ and θ+dθ. Hence,


 to a first order approximation (and becomes exact for a fluid where viscous shear forces are treated as pure contact forces and δr → dr ). If you're happy working with a ring of width δr >0 that is small but
to a first order approximation (and becomes exact for a fluid where viscous shear forces are treated as pure contact forces and δr → dr ). If you're happy working with a ring of width δr >0 that is small but  . That denominator is finite for all finite values of r. So we establish that α(r) = 0 <=>
. That denominator is finite for all finite values of r. So we establish that α(r) = 0 <=>  = 0. Hence, we can find a streamline at radius r (a ring of infinitesimal width if you like) where the flow velocity changes with time while the simplified discussion just continues to talk about rings of a small width and a small net torque on that ring.
= 0. Hence, we can find a streamline at radius r (a ring of infinitesimal width if you like) where the flow velocity changes with time while the simplified discussion just continues to talk about rings of a small width and a small net torque on that ring. is 0 (just to be clear it's everywhere 0, there's no radius r where it could be non-zero or else we can find a ring with net torque on it).
is 0 (just to be clear it's everywhere 0, there's no radius r where it could be non-zero or else we can find a ring with net torque on it). = constant and from equation [4] we must then have
= constant and from equation [4] we must then have  for some constant c => v = (k/r) + c for some constants c,k and v = k/r is the simplest solution.
for some constant c => v = (k/r) + c for some constants c,k and v = k/r is the simplest solution. is the only velocity field that could describe a steady flow free vortex when the fluid has some coefficient of viscosity μ > 0. Thanks again for your time.
is the only velocity field that could describe a steady flow free vortex when the fluid has some coefficient of viscosity μ > 0. Thanks again for your time.