Post by: Jaaanosik on 08/04/2023 21:24:55
Happy Easter!
As the subject says, is proper acceleration absolute?
The answer is yes, because all inertial observers agree on the acceleration that would be measured by an accelerometer.
If we analyze this motion in the rest frame K. We are interested in the A points accelerations.
The A points represent geometric centroids of four 'pie cutouts' of the flywheel.
(https://theelectromagneticnatureofthings.com/wp-content/uploads/2023/03/aa02.png)
Then we calculate the A points accelerations from K'1 and K'2 point of view and compare between the frames.
(https://theelectromagneticnatureofthings.com/wp-content/uploads/2023/04/aa04.png)
The rest frame K starting values are
(https://theelectromagneticnatureofthings.com/wp-content/uploads/2023/04/aa001.png)
The results are perplexing to say the least.
The different inertial observers do not agree on the acceleration.
K'1 moves with speed 1m/s in +X direction in the rest frame K, sees the top of the cycloid.
K'2 moves with speed 1m/s in -X direction in the rest frame K, sees the cusp of the cycloid.
(https://theelectromagneticnatureofthings.com/wp-content/uploads/2023/04/aa006.png)
A3, A4 points have different acceleration in the -y direction, the acceleration is not invariant.
Let us discuss.
Post by: Eternal Student on 08/04/2023 23:29:56
I'll go first:
is proper acceleration absolute?I'll say yes.
Let us discuss.I'm cautious. Looking at the previous posts listed on your profile this is almost exactly the same as another post. You could, for example, have just added a new entry to that old post and it would automatically rise to the top of the forum board as the newest thread to be adjusted.
I'm also really not sure what it was you wanted to discuss. There's few details here with the notable exception being some very nice diagrams. However the diagrams have obviously been used several times before and you've just copied them straight back in here again.
Best Wishes.
Post by: Eternal Student on 09/04/2023 03:43:45
* The points Ai don't seem to have been given the correct co-ordinates to match the diagram.
* K1' and K2' don't seem to be related to the curved yellow lines in the second diagram.
* The table of values at the end is difficult to understand. In the first column, some radius r is changing. What or where is that r?
I'm trying to see what you wanted to discuss but I'm still not sure at the moment, sorry.
Best Wishes.
Post by: Jaaanosik on 09/04/2023 04:59:02
Hi again.There are two sets of coordinates: (X,Y,Z) and (x,y,z)
* The points Ai don't seem to have been given the correct co-ordinates to match the diagram.
* K1' and K2' don't seem to be related to the curved yellow lines in the second diagram.
* The table of values at the end is difficult to understand. In the first column, some radius r is changing. What or where is that r?
I'm trying to see what you wanted to discuss but I'm still not sure at the moment, sorry.
Best Wishes.
This is from a text book:
(https://theelectromagneticnatureofthings.com/wp-content/uploads/2023/03/aa01.png)
General motion of a rigid body in space where reference axes origin attached to B translates and rotates with angular velocity
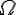 in reference to origin
in reference to origin  . The angular velocity
. The angular velocity 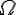 may differ from body angular velocity
may differ from body angular velocity 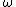 .
.The generic motion equations for velocity and acceleration of point
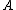 as per the above figure are
as per the above figure are(https://theelectromagneticnatureofthings.com/wp-content/uploads/2023/04/aa008.png)
Please, see the A points coordinates, they are correct, they have small unit vectors (i,j,k), the origin is in point B.
The above equations were used for the calculations.
The radius is the
 where
where  is the curvature of the trajectory.
is the curvature of the trajectory.The K'1 radius for the top of the cycloid is 4m. The K'2 radius for the cusp of the cycloid is going to 0, because the curvature is going to infinity.
The point of discussion are the calculations.
Your questions are excellent, they are important for the calculations.
Edit:
For the rest frame...
(https://theelectromagneticnatureofthings.com/wp-content/uploads/2023/04/aa009.png)
Post by: Eternal Student on 09/04/2023 13:14:59
OK, I can see what you've got know. Rigid body dynamics with an embedded body frame. I'm guessing the point B was the centre of mass of your body.
Basically rigid bodies that start to tumble (rotate) can have accelerations of some parts of the body that are very different to other parts of the body. This allows:
* TV films to be made where space rockets are at risk of being torn apart if the pilot can't stop the craft from tumbling fast enough.
* The "tennis racket" effect or intermediate axis theorem. See the following short YouTube video clip, if you're interested. A tool is set spinning in Zero-G on (....not sure but probably the International Space Station) and exhibits the ability to make very sudden and abrupt flips from head to toe rather than just spinning around one axis as you might have anticipated. With respect to a space craft mentioned above - if the tool was the space capsule and the pilots were located in one end of it, then they are very abruptly accelerated when the head end flips to where the toe end used to be, i.e. they are almost certainly dead.
On a more pedestrian level, tennis rackets will flip in the air when you throw them upwards and spin them around their intermediate axis.
* Gyroscopes and spinning tops can exhibit the fantastic behaviours that they do.
I'm not sure how this connects to "proper acceleration", as defined here: https://en.wikipedia.org/wiki/Proper_acceleration
I haven't checked the mathematics you've presented but, without doubt, parts of the rigid body are experiencing different proper accelerations if it rotates as you've outlined.
Best Wishes.
Post by: Jaaanosik on 09/04/2023 13:48:21
Hi.Correct, these are straight textbook calculations that are the subject of the discussion.
OK, I can see what you've got know. Rigid body dynamics with an embedded body frame. I'm guessing the point B was the centre of mass of your body.
....
Best Wishes.
If somebody has a problem with A points as geometric centroids it is easy to replace the wheel with the rods and some mass at the end of the rods, the blue rods and the blue balls in the first figure.
Post by: alancalverd on 09/04/2023 14:00:14
Quote
In relativity theory, proper acceleration is the physical acceleration (i.e., measurable acceleration as by an accelerometer) experienced by an object.
then edit it a bit to get
proper acceleration is what would be measured by an accelerometer attached to an object
which makes clear and unequivocal sense.
Then if by "absolute" you mean "would be agreed by all observers" the answer is clearly yes, provided that you don't demand simultaneity of observation. The accelerometer in your rocket departing from moon orbit will read and transmit "0.1 g" or something, but nobody on earth will know about it for a second or so after transmission, and if the receiver handshakes "confirm 0.1g" you will transmit "negative, now 0.0" and so forth.
Post by: Jaaanosik on 09/04/2023 15:16:27
...
Then if by "absolute" you mean "would be agreed by all observers" the answer is clearly yes, provided that you don't demand simultaneity of observation.
...
Yet, the calculations show all inertial observes do not agree on the acceleration.
Different inertial observers predict different accelerations based on the textbook calculations.
Post by: alancalverd on 09/04/2023 15:49:42
Post by: Eternal Student on 09/04/2023 16:28:13
Yet, the calculations show all inertial observes do not agree on the acceleration.I'm still not following, sorry.
Different inertial observers predict different accelerations based on the textbook calculations.
You have a formula for the acceleration at point A. All of the things in that formula are determined with reference to the frame K and not K1' or K2'. To get the acceleration with respect to a frame, let's say centred at O at time t=0 and with the offset velocities you have specified, then you still have some work to do. It's not a lot of work, for Galilean relativity or non-relativistic mechanics, the accelerations in those frames are identical to those in the frame K.
Under special relativity, a proper acceleration must, by definition, be measured in the frame where the individual (Sally) was instantaneously at rest. It will not be the same as an acceleration that someone else (Huang) might assign to Sally in the frame where Huang was at rest (unless Huang and Sally were at rest with respect to each other).
Best Wishes.
(Overlap with @alancalverd, who posted before I finished. Looks OK and consistent).
Post by: geordief on 09/04/2023 17:21:07
the data the rocket transmits is absolute acceleration, force per unit massSo a massless body cannot experience that kind of acceleration?
On a personal, intuitive level as a paid up member of the massive travelling public the acceleration I feel I put down to parts of my body being squeezed against other parts as a result of different internal densities .
Is that a correct undetstanding(or something like correct)?
Post by: Jaaanosik on 09/04/2023 23:21:22
Fair enough, because what they see is relative acceleration, i.e. the apparent second derivative of position versus time of an object viewed from a distance, but the data the rocket transmits is absolute acceleration, force per unit mass.
There is no transmission, everything is local.
There is a rest frame inertial observer locally.
There is K'1 frame observer aligned at the same position locally.
There is K'2 frame observer aligned at the same position locally.
Position - meaning space and time are aligned.
All inertial observers are local but they are in the relative motion as described.
There is no distance at play here, no transmission.
All of them are supposed to agree on the acceleration.
Post by: Eternal Student on 09/04/2023 23:32:28
So a massless body cannot experience that kind of acceleration?Being massless has made it considerably more complicated. I think you ( @geordief) need to bring that down to specific examples rather than discussing the situation in general. We would then select a more appropriate system of mechanics that can be applied (e.g. General Relativity).
With simple Newtonian mechanics, a massless body has no inertia or resistance to any force that you think you could apply to it. However, there's no reason to assume it can have any force act on it, all accelerations are possible even without any force. Overall, Newtonian mechanics just will not handle a massless particle.
Best Wishes.
Post by: Jaaanosik on 09/04/2023 23:39:31
Hi.Yet, the calculations show all inertial observes do not agree on the acceleration.I'm still not following, sorry.
Different inertial observers predict different accelerations based on the textbook calculations.
You have a formula for the acceleration at point A. All of the things in that formula are determined with reference to the frame K and not K1' or K2'. To get the acceleration with respect to a frame, let's say centred at O at time t=0 and with the offset velocities you have specified, then you still have some work to do. It's not a lot of work, for Galilean relativity or non-relativistic mechanics, the accelerations in those frames are identical to those in the frame K.
Under special relativity, a proper acceleration must, by definition, be measured in the frame where the individual (Sally) was instantaneously at rest. It will not be the same as an acceleration that someone else (Huang) might assign to Sally in the frame where Huang was at rest (unless Huang and Sally were at rest with respect to each other).
Best Wishes.
(Overlap with @alancalverd, who posted before I finished. Looks OK and consistent).
I showed the calculation for the rest frame in reply #3.
I showed the results for the other frames in my original post, here it is again.
(https://theelectromagneticnatureofthings.com/wp-content/uploads/2023/04/aa006.png)
A3 has 0j in K, A3 has -0.25j in K'1 and A3 has -0.5j in K'2. They are not equal.
A4 has -2j in K, A4 has -1.75j in K'1 and A4 has -1.5j in K'2. They are not equal.
Response to the bold part: they do not agree on the acceleration.
If you are willing, please, show your calculation they are equal, we can compare.
Post by: geordief on 10/04/2023 00:42:12
Hi.It was more an attempt on my part to understand the nature of proper acceleration on massive objects and what describes it in physical terms.So a massless body cannot experience that kind of acceleration?Being massless has made it considerably more complicated. I think you ( @geordief) need to bring that down to specific examples rather than discussing the situation in general. We would then select a more appropriate system of mechanics that can be applied (e.g. General Relativity).
With simple Newtonian mechanics, a massless body has no inertia or resistance to any force that you think you could apply to it. However, there's no reason to assume it can have any force act on it, all accelerations are possible even without any force. Overall, Newtonian mechanics just will not handle a massless particle.
Best Wishes.
(Hoping I can park the question of massless objects even though it was I who introduced it)
If an object is completely rigid and uniformly dense and the acceleration was evenly distributed (this reminds me a bit of gravity) would acceleration affect that body in a fundamentally different way than it would a body where the acceleration would cause internal stresses?
Can we have an idealized acceleration that is indistinguishable from gravity?
Post by: alancalverd on 10/04/2023 09:46:54
So a massless body cannot experience that kind of acceleration?An interesting observation. Classically, a massless body will accelerate instantaneously to infinite speed if you apply an infinitesimal force. Experimentally the only massless "body" is a photon, which travels at c from the instant of its creation. The reconciliation between these statements pretty much occupies the whole of Maxwell and Einstein.
Post by: Eternal Student on 10/04/2023 14:10:30
@geordief , your reply may take some time and sidetrack this thread. I should reply to @Jaaanosik first. I'll put a separate reply for you.
If you are willing, please, show your calculation they are equal, we can compare.Firstly I don't really like the equations you have put down in post #3. I'm not certain they're correct.
(https://theelectromagneticnatureofthings.com/wp-content/uploads/2023/04/aa008.png)
You haven't described what the terms like vB are supposed to be. I'm left guessing it's the velocity vector of the point B in the reference frame K etc. The angular velocities ω and Ω don't seem to go through the right places. It looks like both pass through the point B. I would have expected ω to pass through B and represent a rotation of just the body frame (lower case letters x,y,z) about the centre of mass, while Ω went through the origin, point O, of the fixed axis (with capital letters X,Y,Z for the axis).
I don't think you need the set of equations you have presented at all. There's not much point in adjusting them or writing more of a description about which thing was supposed to be which thing. You just don't need any of it.
Fix the frame K with axis X,Y,Z - it does not rotate, it is a fixed inertial axis system. It can be quite arbitrary, we just want Newton's laws to hold in it - i.e. it should be an inertial frame.
In the frame K, the position vector to an arbitrary point A on the body is rA much as shown in one of your diagram:
(https://theelectromagneticnatureofthings.com/wp-content/uploads/2023/03/aa01.png)
So the velocity vector is
 in the frame K.
in the frame K.The velocity in some other inertial frame like K1' or K2' is just some constant vector added to that, this assumes you are using just Galilean relativity.
So the acceleration in frame K, or frame K1' or K2' is
 because any constant vector differentiates to 0 anyway.
because any constant vector differentiates to 0 anyway.That's it... that's all there is to it. The acceleration of an arbitrary point A on the body (which could be A1 , A2, A3 or A4 in your very first post, is the same in every frame which is just an offset of the frame K. By an "offset" I mean it moves with constant velocity relative to the frame K. As you may know, using Galilean relativity, all inertial frames can be described as these sorts of offsets from each other. So what we are saying is that the acceleration of any point A on the body is the same when measured in ANY inertial reference frame (using Galilean relativity and not Special relativity).
Best Wishes.
Post by: Halc on 10/04/2023 14:38:17
As the subject says, is proper acceleration absolute?The answer is indeed yes, but it has nothing to do with observers or being inertial. An observer not undergoing the acceleration in question would likely compute the proper acceleration of said thing in question and not 'observe' it. All the text in your posts are computations (not always correct ones), and none of them are observations.
The answer is yes, because all inertial observers agree on the acceleration that would be measured by an accelerometer.
Correct, these are straight textbook calculations that are the subject of the discussion.You need to find an actual textbook. The page https://theelectromagneticnatureofthings.com/aa/ is not a textbook and has many severe mistakes and the mathematics presented there is quite wrong. For one, it seems horrible that K is what they call a rest frame and is also used as a unit vector along the Z axis. Use different symbols for these very different things.
You're apparently copying the figures from that page and not doing your own mathematics. The values are wrong for the proper acceleration of almost anything, so it's a poor point to start when trying to analyze the situtation from the perspective of a different frame.
The setup on the website depicts something where the angular momentum is constantly changing, and yet no source of torque on the system is identified. Right there is a red flag that you should be going elsewhere to learn about proper acceleration.
If we analyze this motion in the rest frame K. We are interested in the A points accelerations.
The A points represent geometric centroids of four 'pie cutouts' of the flywheel.
(https://theelectromagneticnatureofthings.com/wp-content/uploads/2023/04/aa001.png)
The first 3 lines seem plausible. The next 4 A values are position coordinates only, not velocities or accelerations. Velocities are given here:
(https://theelectromagneticnatureofthings.com/wp-content/uploads/2023/04/aa002.png)
Looking at A1 column. VB is moving at -1I due to the precession. That's wrong since it's the motion of points A3,A4, and B, but not A1 and A2 which are off to the side, moving faster and not quite perpendicular.
Vrel is the 3rd line, listed as -0.5k, meaning the distance between A and B is 0.25 (not elsewhere specified).
Ω x rA/B seems to be their attempt to correct the discrepancy in the first line, but is done wrong. To get 0.25j, B would need to be right at the origin O and not where the picture puts it. So this middle line is wrong.
I didn't go through the final acceleration calculations since they seem dependent on how the continuous change of angular momentum is being achieved, and that isn't specified. I suspect 'gravity' except they assert that K is an inertial frame, which a lab on Earth is not. If there's gravity, that has to be added to the proper acceleration of each thing, and it isn't.
Quote
The different inertial observers do not agree on the acceleration.No observers are mentioned (correctly so) since proper acceleration isn't frame dependent. The velocities are, but those can be computed trivially by just adding the velocity of the inertial frame to the velocities listed (presuming those figures were correct, which they're not).
Quote
K'1 moves with speed 1m/s in +X direction in the rest frame K, sees the top of the cycloid.
K'2 moves with speed 1m/s in -X direction in the rest frame K, sees the cusp of the cycloid.
Yet, the calculations show all inertial observes do not agree on the acceleration.The fact that you're talking about cycloids and cusps and such seems to indicate analysis of a rolling wheel in freefall and not a precessing gyroscope sort of setup depicted.
It's fine to do this, but then ditch the gyro picture and do an analysis of a wheel rolling with linear motion. I don't see any calculations being done by you, but if they're not coming out with identical acceleration values, it's a big clue that the calculations are being done incorrectly. And again, you seem to be attempting a calculation of different scenario than the one depicted in the OP.
To get the acceleration with respect to a frame,There is no 'acceleration with respect to a frame'. Presuming lack of relativistic spacetime curvature (It all seems to be Newtonian mechanics since nothing particularly relativistic is coming into play in this scenario), acceleration is not dependent on any inertial frame and thus coordinate acceleration is the same as proper acceleration. This is not true of non-inertial frames where coordinate acceleration can be very different than proper acceleration.
And despite the site's claim of frame K being inertial, I suspect it isn't since gyroscopes typically precess under accelerated frames such as a typical lab on the surface of Earth.
So a massless body cannot experience that kind of acceleration?A massless thing (a graviton say) cannot follow a timelike worldline and thus cannot have any notion of proper acceleration. You can bend light around things with fiber optics and such, and I suppose that can be expressed as acceleration, but not proper acceleration.
All that said, proper acceleration seems not to be dependent on mass at all. A 1kg mass following some curved worldline experiences the same proper acceleration as a neutrino following an identical worldline. But a photon cannot follow such a line.
The setup in the OP specifies the mass of none of the components, rightly so because it's irrelevant. The precession rate specified can be achieved with the right mass to moment ratio, but that ratio isn't dependent on the specific mass.
Quote from: Jaaanosik
Is there anything wrong with the analysis?I saw no analysis, just conclusions.
Quote
Did somebody find an error or mistake?Well the acceleration numbers in the OP are self-contradictory. Normally when something like that occurs, the person generating the numbers searches for where the arithmetic mistake was made. But a denialist will declare victory and publish the contradiction.
Another symptom is that this has been an entirely Newtonian exercise, utilizing only Newtonian mathematics to analyze an appropriate (low speed, low mass) situation. But when the mistake is made, you immediately go for relativity theory (not referenced at all before) and not declaring that all physics of the last 3 centuries needs to be discarded.
In Newtonian physics, relative to an inertial frame, and in the absence of gravity, coordinate acceleration and proper acceleration are the same thing. Under special relativity, this isn't true, but the difference is way off in the ~20th digit for a low speed case as is being described here.
I'd also like to say that some vectors are subject to frame translations. An unintuitive example of this is a light pulse could be heading north relative to one inertial frame and east relative to a different inertial frame. This isn't itself contradictory. But it's an example where the same vector (where the light pulse is really going) is expressed quite differently in different reference frames.
The accelerometer must read the same magnitude in any frame, but it's direction might be frame dependent. If you compute different magnitudes, you've made a mistake. You express no interest in finding that, so the topic got moved here. Errors have been pointed out and ignored. Also, the proper accelerations are dependent on the external forces being applied to the system depicted. These have not been identified.
Quote
I agree, the claim the acceleration analysis done here breaks the relativity as we know it, that's a new hypothesis.OK, so you see why I moved things here.
The relativity cannot work unless it is done through a preferred reference frame.
Quote
Is there a physicist who can show the analysis is not good?Start by showing your work. It's really hard to point out the error when the arithmetic is not shown. This also illustrates your denialist attitude. If somebody points out an error, you declare them to be not a physicist, and thus can ignore the comment. If my 8 year old points out where I add 2+5 and get 9, do I dismiss that critique because they're not a professional mathematician?
How did you arrive at the curvature radius value for the cycloids? How did you arrive at the acceleration values from these radius values? Because the radius is indeed frame dependent, but the acceleration isn't.
Let's take a simple case of a wheel rolling along a wall with a permanently vertical axis. You still have points A1-A4 each 0.25 from the axis. In the 'rest frame' K, the wheel spins in place and each point accelerates towards that axis at a fixed magnitude. Now show me how that fixed magnitude changes relative to some other frame where the cycloid radius is different.
Pick several frames, say one where the cusp radius goes to zero, or where the wall is stationary, or where system v is x=1 relative to K, or whatever illustrates your contradiction with Newtonian physics.
If the simple example doesn't illustrate your contradiction, then fine, show the work for the OP case. The object can be forced to take the trajectory described even if takes external forces to do so. I presume that there's no gravity and the origin remains unaccelerated.
Post by: Eternal Student on 10/04/2023 15:21:43
I can see you're still editing your post a little @Halc . Assuming it remains broadly similar to the one I've seen, we seem to be in agreement.
* The acceleration of any point on the body is the same in any inertial reference frame.
* I noticed the diagrams had been taken from the website you mentioned. I didn't even go to the website to have a look at it. It's not a domain name I recognise or would have advised anyone to risk going to visit.
* Considering the mathematics, the diagrams and the equations which were shown, I don't like them either.
* "There is no acceleration with respect to a frame" - yes there is. However it's not relevant in this situation and not worth me making a fuss about. All inertial frames show the same accelerations for any point in the body.
Best Wishes.
Post by: alancalverd on 10/04/2023 16:03:43
An observer not undergoing the acceleration in question would likely compute the proper acceleration of said thing in question and not 'observe' it.Not in my experience. My observer on the ground knows that I am accelerating at 0.8g in a car or pulling 2.5g in a plane because my accelerometer says so and the radio happens to be working today.There's no way he can observe or compute it directly if I am out of sight. Even more the case for a spacecraft telemetry system.
Post by: Jaaanosik on 10/04/2023 16:33:52
... I'm not certain they're correct.
...
They are correct, the textbook:
(https://i.imgur.com/DXoArdR.png)
(https://i.imgur.com/7ZBZjSR.png)

The initial values are posted.
B rotates around O.
The flywheel spins around B.
Quote
...
That's it... that's all there is to it. The acceleration of an arbitrary point A on the body (which could be A1 , A2, A3 or A4 in your very first post, is the same in every frame which is just an offset of the frame K. By an "offset" I mean it moves with constant velocity relative to the frame K. As you may know, using Galilean relativity, all inertial frames can be described as these sorts of offsets from each other. So what we are saying is that the acceleration of any point A on the body is the same when measured in ANY inertial reference frame (using Galilean relativity and not Special relativity).
The acceleration is a function of
 , just see the equations.
, just see the equations.K'1 and K'2 observe different
 values because curvature radius changes, therefore the results are different.
values because curvature radius changes, therefore the results are different.
Post by: Jaaanosik on 10/04/2023 17:24:55
These are just initial values of Omega, omega and positions B and A points with their respective unit vectors.
...
(https://i.imgur.com/4NZpQIB.png)
The first 3 lines seem plausible. The next 4 A values are position coordinates only, not velocities or accelerations.
Quote
Velocities are given here:
(https://i.imgur.com/7QtvIGE.png)
Looking at A1 column. VB is moving at -1I due to the precession. That's wrong since it's the motion of points A3,A4, and B, but not A1 and A2 which are off to the side, moving faster and not quite perpendicular.
Vrel is the 3rd line, listed as -0.5k, meaning the distance between A and B is 0.25 (not elsewhere specified).
Ω x rA/B seems to be their attempt to correct the discrepancy in the first line, but is done wrong. To get 0.25j, B would need to be right at the origin O and not where the picture puts it. So this middle line is wrong.
...
There is no precession. It is straight calculation
 .
.A positions are specified
 , (x,y,z) origin is in B.
, (x,y,z) origin is in B.The
 calculation is correct A1, A2 points are offset to the side they are further away from the Omega axis of rotation compared to A3, A4.
calculation is correct A1, A2 points are offset to the side they are further away from the Omega axis of rotation compared to A3, A4.  are at right angle to
are at right angle to 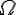 .
.  are parallel to
are parallel to 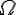 , the results are correct. There is no attempt for any corrections. The calculation is straightforward.
, the results are correct. There is no attempt for any corrections. The calculation is straightforward.  is correct as well.
is correct as well.There is no gravity in this thought experiment.
Quote
The fact that you're talking about cycloids and cusps and such seems to indicate analysis of a rolling wheel in freefall and not a precessing gyroscope sort of setup depicted.
It's fine to do this, but then ditch the gyro picture and do an analysis of a wheel rolling with linear motion. I don't see any calculations being done by you, but if they're not coming out with identical acceleration values, it's a big clue that the calculations are being done incorrectly. And again, you seem to be attempting a calculation of different scenario than the one depicted in the OP.
There are just three inertial frames, with their respective observers, K, K'1, K'2, nothing else.
The cycloids are the consequence of the relative motion between the rest frame K and K'1, K'2.
This it t=0, O, O'1, O'2 are aligned and that's the reason why K'1 and K'2 see different positions on their respective cycloids.
Post by: Eternal Student on 10/04/2023 17:55:52
I've checked again but there's nothing wrong with the derivation given in post #16, which would be about 3 lines if you wrote it out neatly. There are also multiple references for the final result. Here's just two:
https://galileo.phys.virginia.edu/classes/252/lecture1.htm
Which is a short piece of Mathematics, that document was prepared by the University of Virginia
https://plato.stanford.edu/entries/spacetime-iframes/
Which discusses the philosophy along with the mathematics, if you prefer a Philosophical slant. That's a document prepared by Stanford University.
So, I'm really sorry but something does seem to have gone wrong with either the formulae you have used or the arithmetic that was done while applying them.
- - - - - - - - - - - -
I'll address some parts so we can focus on the analysisI appreciate that it can be helpful to identify exactly where you have gone wrong in your calculations. In my own experiences this can be very informative and educational, much more so than just looking at some other method or solution to a problem.
However, I don't have enough time available at the moment. I can't do much more than provide the references given above, sorry.
Best Wishes.
Post by: Jaaanosik on 10/04/2023 19:11:19
Hi.There is more going on with your statement (bold) than one might think. Let us investigate.
I've checked again but there's nothing wrong with the derivation given in post #16, which would be about 3 lines if you wrote it out neatly. There are also multiple references for the final result. Here's just two:
https://galileo.phys.virginia.edu/classes/252/lecture1.htm
Which is a short piece of Mathematics, that document was prepared by the University of Virginia
https://plato.stanford.edu/entries/spacetime-iframes/
Which discusses the philosophy along with the mathematics, if you prefer a Philosophical slant. That's a document prepared by Stanford University.
...
We will discuss only the rest frame K at the moment.
The point B acceleration is (0I,-1J,0K), can we say the point B rotates around origin O1=(0I,-99J,0K) with Omega=(0I,0J,0.1K)?

The B acceleration results are equal for O, O1 but there is a difference between r and Omega values.
(https://i.imgur.com/28GNVi4.png)
Question: Can an observer at B determine what is true origin O or O1 from inside the box without any signal from the outside, assuming the B observer has A points accelerations known to him?
Even more important question: Is
 information lost/destroyed to the B observer inside of the box?
information lost/destroyed to the B observer inside of the box?
Post by: Eternal Student on 10/04/2023 21:43:24
I didn't get around to making a reply for @geordief , sorry.
If an object is completely rigid and uniformly dense and the acceleration was evenly distributed (this reminds me a bit of gravity) would acceleration affect that body in a fundamentally different way than it would a body where the acceleration would cause internal stresses?That is going to take a while to discuss. I'm tempted to suggest creating another thread.
Can we have an idealized acceleration that is indistinguishable from gravity?
Very briefly: There are some differences between a gravitational field that might be produced by a mass and a uniform acceleration. There are articles discussing this and they are based on the idea that a gravitational source should create a force with a gradient (an increase in the magnitude of the force) as you move toward the object. As such there are tidal forces on any object of non-zero width in the region or, to paraphrase it, there are ways to tell if you are in an elevator (without windows) that is being uniformly accelerated or if you were genuinely in a gravitational field. This doesn't cause much problem for General Relativity or "the equivalence principle". It's only necessary to consider local frames and they can be as local, or as small as required.
As regards your question about a body with varying density and stress: All bodies would exhibit stress from tidal forces. You may be considering a related term which is "strain", some objects are stretchy and they will deform under this stress.
Best Wishes.
Post by: geordief on 10/04/2023 22:09:36
Hi.Thanks(I know you are busy so there is no urgency to reply)
I didn't get around to making a reply for @geordief , sorry.If an object is completely rigid and uniformly dense and the acceleration was evenly distributed (this reminds me a bit of gravity) would acceleration affect that body in a fundamentally different way than it would a body where the acceleration would cause internal stresses?That is going to take a while to discuss. I'm tempted to suggest creating another thread.
Can we have an idealized acceleration that is indistinguishable from gravity?
Very briefly: There are some differences between a gravitational field that might be produced by a mass and a uniform acceleration. There are articles discussing this and they are based on the idea that a gravitational source should create a force with a gradient (an increase in the magnitude of the force) as you move toward the object. As such there are tidal forces on any object of non-zero width in the region or, to paraphrase it, there are ways to tell if you are in an elevator (without windows) that is being uniformly accelerated or if you were genuinely in a gravitational field. This doesn't cause much problem for General Relativity or "the equivalence principle". It's only necessary to consider local frames and they can be as local, or as small as required.
As regards your question about a body with varying density and stress: All bodies would exhibit stress from tidal forces. You may be considering a related term which is "strain", some objects are stretchy and they will deform under this stress.
Best Wishes.
I have often heard it said that we measure acceleration in a frame of reference by installing an accelerometer)
What if we dispensed with the accelerometer,?
If we observed any change in relative motion between any two parts of the system in the frame of reference that would indicate acceleration.,I suppose
I think my idea about an infinitely rigid body must be a non starter unless, perhaps we are thinking of point particles (are there point particles with mass?the neutrino?)
Post by: Jaaanosik on 11/04/2023 12:25:42
Hi.Very good post, the 'V' shape of the gravity field lines differs from the straight line uniform acceleration.
I didn't get around to making a reply for @geordief , sorry.If an object is completely rigid and uniformly dense and the acceleration was evenly distributed (this reminds me a bit of gravity) would acceleration affect that body in a fundamentally different way than it would a body where the acceleration would cause internal stresses?That is going to take a while to discuss. I'm tempted to suggest creating another thread.
Can we have an idealized acceleration that is indistinguishable from gravity?
Very briefly: There are some differences between a gravitational field that might be produced by a mass and a uniform acceleration. There are articles discussing this and they are based on the idea that a gravitational source should create a force with a gradient (an increase in the magnitude of the force) as you move toward the object. As such there are tidal forces on any object of non-zero width in the region or, to paraphrase it, there are ways to tell if you are in an elevator (without windows) that is being uniformly accelerated or if you were genuinely in a gravitational field. This doesn't cause much problem for General Relativity or "the equivalence principle". It's only necessary to consider local frames and they can be as local, or as small as required.
As regards your question about a body with varying density and stress: All bodies would exhibit stress from tidal forces. You may be considering a related term which is "strain", some objects are stretchy and they will deform under this stress.
Best Wishes.
The curvature can be detected from within the box.
The same applies to my post above, the curvature radius can be detected.
The flywheel cannot rotate around O1 because the A points accelerations would be different.
The curvature radius is the main factor in the acceleration analysis and this is true even within K frame itself.
Having said that K'1 and K'2 see different flywheel trajectories, they do not agree on the curvature radius with the K frame. Every moving K' sees different curvature trajectory. That's the reason they do not agree on the A points acceleration analysis.
Post by: alancalverd on 11/04/2023 18:06:37
What if we dispensed with the accelerometer,?Something of a problem! In the absence of an external frame we can only measure acceleration as the force per unit mass on a test mass that is free to move inside our accelerating body - i.e. an accelerometer.
Aside from spagettification in a steep gravitational gradient, if an entire rigid object is accelerating uniformly (which can only occur in the case of a flat object perpendicular to a uniform electric, magnetic or gravitational gradient) there is no way any element of it can be aware of its acceleration. The question then arises as to whether you could measure the change in length of a spaghettifying object since all your measuring methods would themselves either be spaghettifying, or constitute an accelerometer!.
Post by: Jaaanosik on 12/04/2023 12:00:30
Did somebody find an error or mistake?
I agree, the claim the acceleration analysis done here breaks the relativity as we know it, that's a new hypothesis.
The relativity cannot work unless it is done through a preferred reference frame.
Is there a physicist who can show the analysis is not good?
The world of physics has some explanation to do.
This does not go away with just moving it to a different sub forum. :)
Post by: Jaaanosik on 13/04/2023 03:12:34
Is there anything wrong with the analysis?I saw no analysis, just conclusions.
...
Reply #3 shows the rest frame calculations that are part of the analysis.
Do you agree with those calculations?
There is no point in checking other frames if we have no agreement in the rest frame.
Reply #23 is continuation of the analysis. It's very important post with implications.
Here are two posts that we can discuss, if interested.
Post by: Jaaanosik on 13/04/2023 18:42:19
No external forces specified, there are no external forces.Reply #3 shows the rest frame calculations that are part of the analysis.Well, I said that the acceleration values could not be known without knowing the external forces being applied to the system. But given the values in that table, one can extrapolate backwards to get the external forces.
Do you agree with those calculations?
This is a closed system and for the sake of the argument we can say in the intergalactic space faraway from any gravity source.
Quote
I agree with the velocity table. Thing is, relative to any other inertial frame, the only values that change on either table is the first line, the IJK one, where the relative velocity of the frame in question is subtracted from those figures. None of the other lines in either table gets effected, so if you're getting different values, there must be a mistake in the calculations.The 2nd line is the second expression from here:
So for instance, in the K'1 frame, the top line would be (-2I, 0J 0K) for each column.
I accept the acceleration table as well. I have comments on those lines
The first line is the acceleration of B at -1J. A nonzero total cannot be without an external force being applied to B large enough to effect that acceleration. I'm not disagreeing with the value, but just wanting to make you aware of this implication of external force being applied.
I don't know what the 2nd line is. It comes to zero for everything. (Ω x rA/B) is the 2nd line of the velocity table, not zero, so that omega with a dot on it must be zero, but I don't know what that symbol means.
(https://i.imgur.com/bI5Jvgl.png)
It is
 ... an angular acceleration, but there is none.
... an angular acceleration, but there is none.Quote
3rd line is the disk spinning about the k axis and the values sum up to zero, so no external forces required.Yes, that's the point, the velocity can be determined by the A points accelerations.
5th line is the spinning of the disk about B, and again the values sum up to zero, so no external forces required.
The 4th line is unnatural and represents a torque in the direction of -i on the system. I agree with the line, but like line 1, can be used to extrapolate an external torque being applied to the system somewhere. This is expected since the setup implies a continuous change of angular momentum which would violate conservation of angular momentum laws without that application of external torque. And yes, this torque causes precession despite your refusal to name it thus.
Bottom line is that the post 3 values are consistent with the scenario.QuoteReply #23 is continuation of the analysis. It's very important post with implications.That was a reply to ES, but I'll try to comment on it.We will discuss only the rest frame K at the moment.No, you can't. If acceleration was fixed at -1J, it would require a velocity relative to O1 of -10I, a contradiction with a velocity a tenth that.
The point B acceleration is (0I,-1J,0K)
Can we say the point B rotates around origin O1=(0I,-99J,0K) with Omega=(0I,0J,0.1K)?
Is that what you were looking for?
Quote
So observer B with help of A points accelerations can determine the velocity, the curvature radius.QuoteQuestion: Can an observer at B determine what is true origin O or O1 from inside the box without any signal from the outside, assuming the B observer has A points accelerations known to him?He knows his acceleration from his accelerometer, so he can point in the direction of O. He can sense the rate of change of that acceleration, so that gives him the ability to triangulate. Yes, he can determine the distance to O. For instance, B goes around O every 6.28 (seconds? units were not clearly given). But if the origin was at a distance of 100, that time would be over a minute.
B observer does not need any signal from the outside to do so, I hope it makes sense.
The question is can the motion satisfy analysis of K frame with curvature radius 1m and at the same time K'1 analysis with curvature radius 4m?
What are the accelerometers at A points going to measure? 1m or 4m radius, because they cannot both.
Post by: Halc on 13/04/2023 23:09:05
No external forces specified, there are no external forces.OK, so you're in denial of Newtonian physics since your assertion violates the first and third laws of motion as well as conservation of angular momentum. Somehow you'll probably blame that on Einstein as well.
This is a closed system and for the sake of the argument we can say in the intergalactic space faraway from any gravity source.
The close system seems to have its center of mass at B, and that center of mass is accelerating, impossible for a closed system.
Yes, that's the point, the velocity can be determined by the A points accelerations.That can't be true else there's be an absolute motion detector. So for circular motion about some axis, one can determine velocity and distance to that axis relative to the frame in which that axis is stationary. That's different than the absolute statement you gave. So our guy on the rolling wheel is always going to measure v=0.5 relative to B, and tangential to the direction of B (r=0.25 away), and no abstract frame change is going to alter that physical measurement.
Quote
Question: Can an observer at B determine what is true origin O or O1 from inside the box without any signal from the outside, assuming the B observer has A points accelerations known to him?OK, I misread this question the first time. The A-point masses define where B is (their mutual center of gravity). If he knows the accelerations of those points, that's the same as the observer at B knowing his own acceleration. All he has to do is average them. That reduces the answer to the one I gave: that B can determine the distance to O by looking at his own instruments instead of those at the A points.
Quote
So observer B with help of A points accelerations can determine the velocity, the curvature radius.He needs no help from the A points to do that, and again, only the velocity relative to O. 'The velocity' and 'the curvature radius' without a frame reference are a meaningless phrases. You said you're only considering frame K at this point, the one in which the axis of Ω is stationary, so in light of that reference, yes the observer at B can determine those things, and without help.
Quote
The question is can the motion satisfy analysis of K frame with curvature radius 1m and at the same time K'1 analysis with curvature radius 4m?It can't determine velocity relative to an unspecified frame. If B is told to add 1I to all his velocity computations, then sure, he can say his velocity now ranges from 2 to zero relative to this new frame in which the Ω axis is moving at speed -1I. But that's giving him the answer. He doesn't measure that.
Quote
What are the accelerometers at A points going to measure?Those are objective facts, physical measurements. They read what your chart says in post 3, minus the axis labels. They cannot read one thing and also read a different one. That would be a logical contradiction.
So for instance, in the OP scenario at t=0, the accelerometer at A4 reads 2.236, and thataway, a direction of a point that you happen to assign the coordinate (X=0 Y=0, Z=0.25), but the meter is unaware of those coordinates. It just displays an arrow pointing that way, essentially what a plumb bob does (except it points the opposite way). That, plus the magnitude, is your physical data, and it must be the same regardless of abstract frame choice.
Quote
1m or 4m radius, because they cannot both.Accelerometers read a vector acceleration, not a scalar length. Meters is the wrong unit for an accelerometer to read. You might want to put one additional instrument next to it reading the derivative of the accelerometer. For the rolling wheel, it (the ones at A points) would read zero for the magnitude change and ω for the rate of direction change. For the complicated setup in the OP, the meters would both be bouncing all over the place and there would be no simple way to determine the center of anything from such unstable readings, but it gets easy if you combine (average) the readings at all 4 A points.
Post by: Jaaanosik on 14/04/2023 03:19:27
The origin O is the barycenter of the closed system, that's where is the center of mass, not B.No external forces specified, there are no external forces.OK, so you're in denial of Newtonian physics since your assertion violates the first and third laws of motion as well as conservation of angular momentum. Somehow you'll probably blame that on Einstein as well.
This is a closed system and for the sake of the argument we can say in the intergalactic space faraway from any gravity source.
The close system seems to have its center of mass at B, and that center of mass is accelerating, impossible for a closed system.
O is the origin of the inertial system.
There is no denial of Newtonian physics or conservation of angular momentum.
Quote
This calculation is for 100m curvature radius:Yes, that's the point, the velocity can be determined by the A points accelerations.That can't be true else there's be an absolute motion detector. So for circular motion about some axis, one can determine velocity and distance to that axis relative to the frame in which that axis is stationary. That's different than the absolute statement you gave. So our guy on the rolling wheel is always going to measure v=0.5 relative to B, and tangential to the direction of B (r=0.25 away), and no abstract frame change is going to alter that physical measurement.
(https://i.imgur.com/JEB0W3x.png)
This is the calculation for 1m curvature radius:
(https://i.imgur.com/hMVGSzV.png)
This is the calculation for 4m curvature radius:
(https://i.imgur.com/qt08MCn.png)
A3, A4 points acceleration values determine B, A points velocity and the curvature radius, nothing else is required.
The acceleration is absolute, only one set of values can be on A3 accelerometer and A4 accelerometer.
Quote
The bold part, please, see the calculation above.QuoteQuestion: Can an observer at B determine what is true origin O or O1 from inside the box without any signal from the outside, assuming the B observer has A points accelerations known to him?OK, I misread this question the first time. The A-point masses define where B is (their mutual center of gravity). If he knows the accelerations of those points, that's the same as the observer at B knowing his own acceleration. All he has to do is average them. That reduces the answer to the one I gave: that B can determine the distance to O by looking at his own instruments instead of those at the A points.QuoteSo observer B with help of A points accelerations can determine the velocity, the curvature radius.He needs no help from the A points to do that, and again, only the velocity relative to O. 'The velocity' and 'the curvature radius' without a frame reference are a meaningless phrases. You said you're only considering frame K at this point, the one in which the axis of Ω is stationary, so in light of that reference, yes the observer at B can determine those things, and without help.
The acceleration is absolute therefore the acceleration determines the velocity and the curvature radius.
Quote
QuoteThe question is can the motion satisfy analysis of K frame with curvature radius 1m and at the same time K'1 analysis with curvature radius 4m?It can't determine velocity relative to an unspecified frame. If B is told to add 1I to all his velocity computations, then sure, he can say his velocity now ranges from 2 to zero relative to this new frame in which the Ω axis is moving at speed -1I. But that's giving him the answer. He doesn't measure that.QuoteWhat are the accelerometers at A points going to measure?Those are objective facts, physical measurements. They read what your chart says in post 3, minus the axis labels. They cannot read one thing and also read a different one. That would be a logical contradiction.
So for instance, in the OP scenario at t=0, the accelerometer at A4 reads 2.236, and thataway, a direction of a point that you happen to assign the coordinate (X=0 Y=0, Z=0.25), but the meter is unaware of those coordinates. It just displays an arrow pointing that way, essentially what a plumb bob does (except it points the opposite way). That, plus the magnitude, is your physical data, and it must be the same regardless of abstract frame choice.
(https://i.imgur.com/4H4WJpZ.png)
If this board is placed on a table it will measure the gravity, if rotated, different axis will measure the gravity.
Accelerometers measure absolute acceleration.
This board is calibrated for m/s^2.
Quote
Quote1m or 4m radius, because they cannot both.Accelerometers read a vector acceleration, not a scalar length. Meters is the wrong unit for an accelerometer to read. You might want to put one additional instrument next to it reading the derivative of the accelerometer. For the rolling wheel, it (the ones at A points) would read zero for the magnitude change and ω for the rate of direction change. For the complicated setup in the OP, the meters would both be bouncing all over the place and there would be no simple way to determine the center of anything from such unstable readings, but it gets easy if you combine (average) the readings at all 4 A points.
Post by: Jaaanosik on 14/04/2023 16:49:28
...I pointed out in my Reply #23QuoteThis calculation is for 100m curvature radiusThese numbers are fiction. For instance, top line lists VB at -10I where in fact at r=100m and Ω=1, VB would be -100I.
So you're trying to compute stuff possibly from a curvature, but the curvature doesn't give any indication of how fast somethings is traversing that curve. It could be anything. You made up some numbers. Ω wasn't held constant, and neither was any of the proper accelerations, so it wasn't based on those.
 and it follows
and it follows  so the flywheel maintains its absolute rotation around K, k axis because 0.1 + 0.9 = 1Ω.
so the flywheel maintains its absolute rotation around K, k axis because 0.1 + 0.9 = 1Ω.So to expand, the analysis goes backwards.
(https://i.imgur.com/JEB0W3x.png)
The A3, A4 accelerations are measured and the values are above.
What is the B velocity if B acceleration is known (above)? The first line in the velocity table because that's the only possible calculation.
It cannot be 1m/s (or anything else) because it would require to have different A3, A4 points acceleration, see the table bellow.
(https://i.imgur.com/hMVGSzV.png)
The direction of the acceleration in B points towards the origin and the radius is how far is the origin.
Once we know velocity and the acceleration we get the curvature radius from
(https://i.imgur.com/MO0fBu0.png)
It is crucial to resolve this part of analysis in order to discuss anything else further.
Post by: GertrudeFranklin on 14/04/2023 17:47:03
Post by: Jaaanosik on 14/04/2023 20:01:53
What a detailed explanation with calculus. Thanks!It appears to me your potential questions got answered, not dismissed. :)
I came on the thread and were ready to post a few questions, but your last post dismissed them all.
Thank you another time! :)
It is good to have questions.
The calculations are based on textbooks, the main questions are what input parameters where used, that is important.
What parameters, why those parameters,... more things to uncover.
The calculations can be checked by anybody with the input parameters layed out.
If there is something new then I am going to say it is new, as in my post #28.
I am not claiming it is a theory, because I see it as a hypothesis. After a review a hypothesis can become a theory if agreed by reviewers.
An example, we know that information cannot be destroyed in QM:
https://en.wikipedia.org/wiki/No-hiding_theorem#Conservation_of_quantum_information
So here is a hypothesis:
The information about velocity and curvature radius cannot be hidden/destroyed in classical physics, mechanical systems.
It is conserved in the absolute proper acceleration.
Wouldn't it be nice to get a unification/agreement between QM and classical physics? ;)
Post by: Halc on 14/04/2023 22:39:27
OK, I think I actually finally see what you're trying to do, and where your mistakes are. Rotation (as well as acceleration) being absolute means they cannot be frame dependent. So Ω and ω must remain 1 and 2 respectively. To suggest otherwise is to say that it takes a different amount of time to go all the way around relative to another frame. Spin rates cannot change under Newtonian mechanics, so Ω and ω are fixed.and it follows
so the flywheel maintains its absolute rotation around K, k axis because 0.1 + 0.9 = 1Ω.
What you describe is a pseudo-rotation radius based on the momentary frame-dependent curvature of the trajectory of a point on a cycloid. That's a valid (albeit pretty complicated) way to go about it, but assign it a new symbol. Don't overload Ω like you've done since Ω is fixed at 1 (and the instruments at B can measure it directly). So call it δ or something. Then the equations will work out and you get the correct answer for any frame.
The r=4 acceleration line matches the (wrong) values from post 3, so I'll use that one as my example with corrected values.
Values for motion of B are relative to the K'1 frame where the pseudo-rotation about the stationary axis at (0, 0, -3) at rate δ which is 0.5. Other values are relative to B and not the frame of choice.
VB = (-2I, 0, 0) ( 4δ )
All the other velocity lines still reference Ω or ω and not δ and are relative to B, not relative to any chosen frame, so they remain the same as the K values in post 3 which are
Ω x rA/B ¼j -¼j 0 0 (precession rate, a function of Ω, not of δ)
vrel -½k ½k ½i -½i (spin velocity due to ω)
A similar adjustment to the acceleration lines. First one is based on δ, the rest on Ω or ω
aB = -1J (centripetal due to δ)
Ω² x rA/B = -¼i, ¼i, 0, 0 (centripetal accel due to Ω)
2Ω x vrel = 0, 0, 1j, -1j (from torque causing precession rate Ω)
arel = -i, i, -k, k (centripetal acceleration due to ω)
The sum of these is identical in any frame. In fact, except for the VB line, all lines are the same, and the accelerations are not in any way a function of VB.
You should have realized that a mistake was made when the acceleration results came out frame dependent like that, different in both magnitude and direction.
For instance, A3 accelerates at 1 m/sec² but in the K2 frame it comes out to 1.096 m/sec² and pointing 14° in a different direction. That violates these values being objective. You seem to persist in asserting that the meter at B reads two different things, a logical contradiction. So consider my correction to your analysis above.
Post by: Jaaanosik on 15/04/2023 19:23:20
Thanks Halc, now we are getting into the inner workings...OK, I think I actually finally see what you're trying to do, and where your mistakes are. Rotation (as well as acceleration) being absolute means they cannot be frame dependent. So Ω and ω must remain 1 and 2 respectively. To suggest otherwise is to say that it takes a different amount of time to go all the way around relative to another frame. Spin rates cannot change under Newtonian mechanics, so Ω and ω are fixed.and it follows
so the flywheel maintains its absolute rotation around K, k axis because 0.1 + 0.9 = 1Ω.
What you describe is a pseudo-rotation radius based on the momentary frame-dependent curvature of the trajectory of a point on a cycloid. That's a valid (albeit pretty complicated) way to go about it, but assign it a new symbol. Don't overload Ω like you've done since Ω is fixed at 1 (and the instruments at B can measure it directly). So call it δ or something. Then the equations will work out and you get the correct answer for any frame.
The r=4 acceleration line matches the (wrong) values from post 3, so I'll use that one as my example with corrected values.
Values for motion of B are relative to the K'1 frame where the pseudo-rotation about the stationary axis at (0, 0, -3) at rate δ which is 0.5. Other values are relative to B and not the frame of choice.
VB = (-2I, 0, 0) ( 4δ )
All the other velocity lines still reference Ω or ω and not δ and are relative to B, not relative to any chosen frame, so they remain the same as the K values in post 3 which are
Ω x rA/B ¼j -¼j 0 0 (precession rate, a function of Ω, not of δ)
vrel -½k ½k ½i -½i (spin velocity due to ω)
A similar adjustment to the acceleration lines. First one is based on δ, the rest on Ω or ω
aB = -1J (centripetal due to δ)
Ω² x rA/B = -¼i, ¼i, 0, 0 (centripetal accel due to Ω)
2Ω x vrel = 0, 0, 1j, -1j (from torque causing precession rate Ω)
arel = -i, i, -k, k (centripetal acceleration due to ω)
The sum of these is identical in any frame. In fact, except for the VB line, all lines are the same, and the accelerations are not in any way a function of VB.
You should have realized that a mistake was made when the acceleration results came out frame dependent like that, different in both magnitude and direction.
For instance, A3 accelerates at 1 m/sec² but in the K2 frame it comes out to 1.096 m/sec² and pointing 14° in a different direction. That violates these values being objective. You seem to persist in asserting that the meter at B reads two different things, a logical contradiction. So consider my correction to your analysis above.
First, just some thought exercise: Can we define Ω without a radius? Can we have radian without a radius?
If I understand correctly you are suggesting to name B orbital angular velocity δ and the value is 0.5 for 4m radius.
... and B spin angular velocity Ω=1, right?
Let us use your suggestion for the following calculation.
We take the flywheel alone and it falls in a 'circular' orbit around the Earth. The flywheel is flat.
(https://i.imgur.com/ekdbWqe.png)
We just replace O with the center of the Earth r=7000km, that is the distance between B and the center of the Earth.
(https://i.imgur.com/taU3qrl.png)
The gravitational acceleration is 8.13475m/s^2 at that height.
If we go by the current GR there is no force acting on B, B observer is inertial by definition and the flywheel rotates around B.
We define Ω=(0,0,0) and to get some reasonable numbers let us increase ω=(0,200,0).
The current understanding of the physics says, there is only centripetal force from A points to B, nothing else.
Now let us examine an idea, what if gravity is a force and not curved space.
The calculation Ω=(0, 0, 0.001078011) and ω=(0, 200, -0.001078011) and r=7000000m, the flywheel dimensions are the same.
(https://i.imgur.com/K6Rgp0E.png)
Your argument should be δ=(0, 0, 0.001078011) generates gravity centripetal force at B and it is negated by centrifugal force of the same magnitude, so there is no force acting on B and your Ω=(0,0,0); so there is only centripetal force on the flywheel to B, correct?
My calculation is different, it predicts a torque. This torque generates a precession, speed up of the flywheel orbit. If the flywheel rotates opposite way the calculation predicts recession, slow down of the flywheel orbit.
This has been settled by 'experiments' - satellite flyby anomalies: https://en.wikipedia.org/wiki/Flyby_anomaly
The satellites have reaction wheels on them for positioning/turning.
The GR cannot explain it, satellites speed ups and slow downs, my calculation can.
The hypothesis: The gravity is a real force.
Post by: Halc on 15/04/2023 23:11:17
Thanks Halc, now we are getting into the inner workings...Well, no, now we're kind of done. The corrected calculation is shown, and it is also incomplete and doesn't work for frames with motion along the Y axis. You'd need another line to do it with your funny cycloid method because motion along a trochoid path isn't at a constant rate like it is for a circular path, so a component for the acceleration needed for those speed changes needs to be there. The component is zero if no Y motion is present, so the answer works.
Quote
Can we define Ω without a radius?Of course. Ω here is just 2 rads/sec which makes no mention of radius, and is actually used with different radii in the numbers you put in post 3. It is a vector, so the direction of the axis is part of Ω, and is presumably north in the orbity thing below, but most satellites do not orbit about that axis.
Quote
If I understand correctly you are suggesting to name B orbital angular velocity δ and the value is 0.5 for 4m radius.Yes for the 0.5 and 4m radius, but it isn't an orbital velocity since B isn't orbiting anything 4 meters away. B doesn't actually orbit anything, which is a word reserved for a sort of a gravity/satellite relationship. B traces a circular path around O (the origin of frame K), and since the disk with centroid at B has changing angular velocity, that circular motion is precession about O, not an orbit about O.
B never revolves, precesses, or orbits about the pseudo-point at K=-3 in K'1, even if its motion maintains a constant distance from that point for a moment.
Quote
B spin angular velocity Ω=1, right?The disk defining B spins at ω=2. B precession angular velocity is Ω=1. I'm agreeing with you, but wording it more correctly.
Quote
We take the flywheel alone and it falls in a 'circular' orbit around the Earth. The flywheel is flat.But there's no bar running from O this time applying torque to the disk, so the disk won't precess. It will just spin on the x axis permanently as it orbits. There's a lot of satellites that do this. None of them precess.
We just replace O with the center of the Earth r=7000km, that is the distance between B and the center of the Earth.
Quote
The gravitational acceleration is 8.13475m/s^2 at that height.You're mixing theories here. Under Newton there is gravitational acceleration since gravity is a force, and F=ma. Under GR there is no force and no acceleration and the spinning disk follows a geodesic through curved spacetime. Either way, the proper acceleration of B is zero, but the coordinate acceleration is around 8, assuming a sort of semi-inertial coordinate system that Newton might have used, or possibly a rotating reference frame that most people use from day to day.
If we go by the current GR there is no force acting on B
Quote
B observer is inertial by definitionLocally inertial since he experiences negligible proper acceleration. In a larger coordinate system (one that includes Earth), it's not inertial because spacetime isn't Minkowskian there.
Quote
We define Ω=(0,0,0)The flywheel is not in orbit, but just hovering over Earth? That makes no sense.
Quote
and to get some reasonable numbers let us increase ω=(0,200,0).~1910 RPM. OK...
Quote
The current understanding of the physics says, there is only centripetal force from A points to B, nothing else.It's a disk. The forces are from every direction, not just 4 points. There are differences, and ones that should be taking into account in your post 3 calculation but are not. The answer there is a good approximation, but since the disk has more angular moment about the k axis than does the collection of 4 point masses, some of the lines (notably the torque one) need a bit of adjustment.
I'm saying all this because I don't want you pointing back to my post saying that I agreed to something which is only approximately correct. So on that note, the centripetal force from all the mass of the disk adds up to zero, and so has no effect on B. B could be severed from the A points (becoming a small dot of matter surrounded by a detached spinning disk with a slightly larger hole in it) and the motions of everything would be essentially unaffected by this. The A points act on and cancel out each other and don't really have much if any effect on B. This is not true in the OP example where the A points applied lateral force and also torque to B which B had to transfer down the axle to O where the hidden parts of the close system could deal with them. That isn't happening with B in the sky.
Now let us examine an idea, what if gravity is a force and not curved space.
The calculation Ω=(0, 0, 0.001078011) and ω=(0, 200, -0.001078011)[/quote]Sorry, you changed ω. Pick one. And what's the point of tilting the disk slightly like that?
Also, 7 significant digits seems too many for a simple example. How about 3.9 rads/hr for Ω?
and r=7000000m, the flywheel dimensions are the same.
(https://i.imgur.com/K6Rgp0E.png)
Quote
Your argument should be δ=(0, 0, 0.001078011) generates gravity centripetal force at BDon't presume to tell me what my argument should be. If we're talking the frame of the CoG of Earth, then δ and Ω are the same thing. So it's just Ω. Secondly, there's no such thing as gravity centripetal force. In Newtonian physics, there is no centripetal force on a satellite, only gravity. The accelerometer would be nonzero if there was centripetal force. Under GR, there is no force at all, centripetal, gravitational, or otherwise. So B has zero proper acceleration in both cases.
Quote
and it is negated by centrifugal forceThere is no centrifugal force at all here. That's only meaningful in a rotating reference frame, and nobody has specified such a frame here.
Quote
My calculation is different, it predicts a torque. This torque generates a precession, speed up of the flywheel orbit.Precession doesn't change the orbit altitude. It changes either the angular momentum direction of the spinning object or the direction of the orbital axis, or other variants like the precession of the major axis of an eccentric orbit, all quite normal things. I don't know what you mean by 'speed up'. Does the orbit gain or lose energy? Speed-up usually means a loss of orbital energy, in which case you need to show where that goes.
The link you give has to go with gravitational boosts of a flyby (like what the Voyager probes did with Jupiter and most of the other planets) to gain far more speed than could be provided by the limited propulsion system. It has nothing to do with orbits, which are not known to gain energy from nowhere.
How is this relevant to the topic here? You posted contradictory stuff. It takes 38 posts to figure out what you actually did, it was corrected, apparently to your dismay. So instead of learning, you go off and propose a new thing, this 'my calculation' which is strangely (but not unexpectedly) unspecified. Let me know how it works out.
Post by: hamdani yusuf on 17/04/2023 14:29:10
As the subject says, is proper acceleration absolute?
The answer is yes, because all inertial observers agree on the acceleration that would be measured by an accelerometer.
Accelerometers in ISS show near zero values, although it's accelerated toward the earth center significantly.
Quote
Gravity at the altitude of the ISS is approximately 90% as strong as at Earth's surface, but objects in orbit are in a continuous state of freefall, resulting in an apparent state of weightlessness.
https://en.wikipedia.org/wiki/International_Space_Station
Post by: Jaaanosik on 17/04/2023 16:02:17
...
How is this relevant to the topic here? You posted contradictory stuff. It takes 38 posts to figure out what you actually did, it was corrected, apparently to your dismay. So instead of learning, you go off and propose a new thing, this 'my calculation' which is strangely (but not unexpectedly) unspecified. Let me know how it works out.
The point of contention is the relationship between orbit and spin angular velocities.
So a simplification, disc spinning in an intergalactic space as per the op but there is no rod, no centripetal acceleration.
What are the A points accelerations when we consider two sets of input parameters:
1. Ω=(0,0,1), ω=(0,2,0)
2. Ω=(0,0,0), ω=(0,2,1)
In both cases the flywheel has the same rotation around K,k.
Are the A points accelerations going to be the same in both instances?
Post by: Jaaanosik on 17/04/2023 22:03:55
...QuoteSo a simplification, disc spinning in an intergalactic space as per the op but there is no rod, no centripetal acceleration.Spins cannot have two values, so this makes no sense.
What are the A points accelerations when we consider two sets of input parameters:
1. Ω=(0,0,1), ω=(0,2,0)
2. Ω=(0,0,0), ω=(0,2,1)
...
I'll try to ask the question differently.
We start with the rotation and spin as per OP, so we have Ω=(0,0,1), ω=(0,2,0).
At time t=0 we cut the B from the rod and we are left with the spinning wheel.
Is ω=(0,2,1) the correct spinning wheel initial angular velocity after the cut?
Post by: Halc on 17/04/2023 23:54:31
The point of contention is the relationship between orbit and spin angular velocities.There is no relationship, at least not directly. There are secondary effects. For instance, Earth's rotation rate ω is once every 23:56:04 hours, but the direction of that rotation (axis orientatin) precesses at a rate Ω of about once every 26000 years, and not all the way around like your spinning top, but only in a more narrow cone. So Polaris will once again become the north star in about 26000 years, and it's actually a pretty freaky chance that our axis happens to point so close to such a bright star right now. This precession is due to external torque from tidal forces from both the moon and sun.
Quote
So a simplification, disc spinning in an intergalactic space as per the op but there is no rod, no centripetal acceleration.Spins cannot have two values, so this makes no sense.
What are the A points accelerations when we consider two sets of input parameters:
1. Ω=(0,0,1), ω=(0,2,0)
2. Ω=(0,0,0), ω=(0,2,1)
There's just ω, and absent external forces, unstable shaped objects (like tennis racquets, wingnuts and such), it is constant for rigid objects like a disk. Orbits have no direct effect on it. Note it must be a rigid object. You can spin a water bottle at ω along its long axis and after a short time it's spin axis will remain the same, but the rate will drop considerably to perhaps 0.3ω as the bottle reorients itself differently relative to that spin axis. Angular momentum is conserved, but not always angular velocity.
Quote
In both cases the flywheel has the same rotation around K,k.No. Ignoring the meaningless Ω value and taking the ω as the spin, you've specified the first one rotating at 2 around the L axis, and the second one rotating faster at about 2.236 around an axis tilted upward 14 degrees. This would become more clear if you expressed ω in polar coordinates instead of rectangular coordinate that you have there.
Polar coordinates of your ω values above are (in magnitude, deg, deg) respectively
(2, 90, 0)
(2.236, 90, 14.4) .
Quote
Are the A points accelerations going to be the same in both instances?Presuming they're both at the same distance from the axis, the 2nd one will have greater acceleration magnitude due to the higher spin rate, but they'll all accelerate towards the axis of the spinning disk, unlike the example with the precession due to internal forces acting on the depicted parts.
Accelerometers in ISS show near zero values, although it's accelerated toward the earth center significantly.That's right. Accelerometers display proper acceleration, not coordinate acceleration. The ISS has only coordinate acceleration towards Earth.
At time t=0 we cut the B from the rod and we are left with the spinning wheel.It can't speed up (to 2.236) like that, but it did very much have a k component to its motion due to a fairly high precession rate (significant torque being applied). That would result in unstable motion, a disk spinning on a different axis than the one perpendicular to its face. It would wobble and not have a defined spin rate, but it would have a defined (constant) angular momentum axis perhaps something in the neighborhood of 10° up from the y axis or something. That's just a guess. I'm not sure if it would be accurate to specify an angular velocity to your wobbling disk since it continuously changes and the acceleration of a given point on it does not point perpendicular to the axis. None of the usual trivial formulas would apply, and only some fairly involved calculus would be able to compute the acceleration of a given A point.
Is ω=(0,2,1) the correct spinning wheel initial angular velocity after the cut?
Consider the solar system. It has definite constant angular momentum on an axis more or less corresponding to the orbital plane of the planets. The majority of that angular momentum is accounted for by Jupiter (more than everything else combined). But the solar system has no angular velocity. There's no rate at which the solar system revolves due to it not being a rigid object. But neither do even unstable rigid objects like the wingnut I mentioned. A disk spinning on a skewed axis would exhibit predictable but not regular angular motion.
Post by: Jaaanosik on 18/04/2023 02:11:59
There is no speed up, it is already at that speed because absolute Ω and absolute ω add up.At time t=0 we cut the B from the rod and we are left with the spinning wheel.It can't speed up (to 2.236) like that, but it did very much have a k component to its motion due to a fairly high precession rate (significant torque being applied).
Is ω=(0,2,1) the correct spinning wheel initial angular velocity after the cut?
Ω=(0,0,1), ω=(0,2,0)
Ω+ω=(0,2,1)
Quote
That would result in unstable motion, a disk spinning on a different axis than the one perpendicular to its face. It would wobble and not have a defined spin rate, but it would have a defined (constant) angular momentum axis perhaps something in the neighborhood of 10° up from the y axis or something. That's just a guess. I'm not sure if it would be accurate to specify an angular velocity to your wobbling disk since it continuously changes and the acceleration of a given point on it does not point perpendicular to the axis. None of the usual trivial formulas would apply, and only some fairly involved calculus would be able to compute the acceleration of a given A point.The equations calculate the instantaneous acceleration.
After some delta time dt there is a torque that generates dΩ this would translate into a feedback loop...
That's the complication, agreement here.
Quote
Consider the solar system. It has definite constant angular momentum on an axis more or less corresponding to the orbital plane of the planets. The majority of that angular momentum is accounted for by Jupiter (more than everything else combined). But the solar system has no angular velocity. There's no rate at which the solar system revolves due to it not being a rigid object. But neither do even unstable rigid objects like the wingnut I mentioned. A disk spinning on a skewed axis would exhibit predictable but not regular angular motion.
Post by: Jaaanosik on 20/04/2023 20:13:44
The 'orbital' Ω is responsible for the acceleration at point B.
The 'spin' ω=(0,2,0) does not contribute to B point acceleration despite having j non-zero value.
(https://i.imgur.com/ndlKmp4.png)
The point B circle trajectory (left), point B straight line uniform acceleration trajectory (right).
The acceleration magnitude at point B is the same and the spinning disc does not rotate around z axis at point B in all instances.
(https://i.imgur.com/37GYS1c.png)
The calculations show the trajectory curvature radius can be deduced from A points accelerations and no signal from the outside is required.
Post by: Jaaanosik on 21/04/2023 17:23:28
...Just pointing out, δ is your invention, your hypothesis.
What you describe is a pseudo-rotation radius based on the momentary frame-dependent curvature of the trajectory of a point on a cycloid. That's a valid (albeit pretty complicated) way to go about it, but assign it a new symbol. Don't overload Ω like you've done since Ω is fixed at 1 (and the instruments at B can measure it directly). So call it δ or something. Then the equations will work out and you get the correct answer for any frame.
...
The textbooks are clear, there are only Ω and ω.
(https://i.imgur.com/7ZBZjSR.png)
Post by: Jaaanosik on 22/04/2023 19:41:43
...The bold part...
What you describe is a pseudo-rotation radius based on the momentary frame-dependent curvature of the trajectory of a point on a cycloid. That's a valid (albeit pretty complicated) way to go about it, but assign it a new symbol. Don't overload Ω like you've done since Ω is fixed at 1 (and the instruments at B can measure it directly). So call it δ or something. Then the equations will work out and you get the correct answer for any frame.
...


If
 and
and  then
then  (skipping the other obvious dimensions).
(skipping the other obvious dimensions).(https://i.imgur.com/prXV9EO.png)
K'1 and K'2 frame curvature radius values are eliminated.
... and it is a contradiction to K'1 and K'2 because K'1
 and K'2
and K'2  .
.That's a problem, the rest frame K with
 and
and  has become the preferred frame.
has become the preferred frame.There goes the relativity out of the window and I don't have a problem with that. :)
We just have to settled on one preferred reference frame. ;)
Post by: Jaaanosik on 24/04/2023 16:59:27
Any undergraduate students here?
Brave enough to ask these questions their professors? ;)
Post by: Jaaanosik on 26/04/2023 12:33:30
over 90% percent of what I said is textbook stuff.
I made obvious controversial conclusions that are logical.
Are you going to help the truth to come out?
Post by: Halc on 26/04/2023 14:08:57
over 90% percent of what I said is textbook stuff.I disagree with that since I see no mention of your funny trochoid analysis in the one page of book you show.
If you're going to use trochoid mathematics for the acceleration of point B, you also need to use it for the A points, but you're not doing that. None of that is in the tiny bit of textbook you mention although I imagine it's covered somewhere.
Anyway, I stopped contributing since all the answers are already above and you purpose seems to be to demonstrate physics to be wrong and not to figure out where the error is in your calculations.
Quote
Are you going to help the truth to come out?I did, and done correctly there are no contradictions. The error has been pointed out. Stop defending something the textbook doesn't say and understand the corrections.
Post by: Jaaanosik on 26/04/2023 14:35:56
The generic motion equations are used for an instantaneous acceleration calculations and they are supposed to work for any inertial observer if the relativity is true.over 90% percent of what I said is textbook stuff.I disagree with that since I see no mention of your funny trochoid analysis in the one page of book you show.
If you're going to use trochoid mathematics for the acceleration of point B, you also need to use it for the A points, but you're not doing that. None of that is in the tiny bit of textbook you mention although I imagine it's covered somewhere.
Anyway, I stopped contributing since all the answers are already above and you purpose seems to be to demonstrate physics to be wrong and not to figure out where the error is in your calculations.QuoteAre you going to help the truth to come out?I did, and done correctly there are no contradictions. The error has been pointed out. Stop defending something the textbook doesn't say and understand the corrections.
Generic curved trajectory has two accelerations, normal and tangential.
The point B is at the top of the cycloid in K'1 frame and there is only pure normal/centripetal acceleration, there is no tangential acceleration.
The curvature radius is 4m in K'1 frame and your correction of insisting that Ω=1 invalidates this curvature radius because the acceleration in B should be rΩ^2 = 4m/s^2.
The radius r=1m is in the rest frame and you are making it the preferred frame of analysis.
There is pure tangential acceleration in K'2 frame, don't you see it?
Your correction is wrong and it is there for others to see.
The instantaneous acceleration at any other point on the cycloid has to consider correct normal and tangential accelerations in any given frame.
Post by: Eternal Student on 26/04/2023 21:41:46
I've had several attempts at writing a reply BUT I wasn't sure it would make any difference.
What sort of reply or response would you like?
Are you going to help the truth to come out?I do not have Sean Carroll (a physicist) in my friends list or anything like that. There are limits on what I could do.
Let's not consider your idea for a moment, just consider an arbitrary idea presented by some person in the world. Is it efficient to get the world's leading physicists to apply their time to look at all these people's ideas? Isn't it more efficient for them to concentrate on peer-reviewed research papers in the journals? Now, sometimes a good idea that appeared on a forum is going to be missed. That's a shame, don't get me wrong, that is a real shame - but if all the physicists were reading forums instead of journals then hardly any new research gets done by them and that seems to be a much greater loss.
This forum is quite small, there aren't many users, who do you think is here and what do you think they can or should do?
Best Wishes.
Post by: Jaaanosik on 27/04/2023 16:38:45
Hi.To keep an open mind.
I've had several attempts at writing a reply BUT I wasn't sure it would make any difference.
What sort of reply or response would you like?Are you going to help the truth to come out?I do not have Sean Carroll (a physicist) in my friends list or anything like that. There are limits on what I could do.
Let's not consider your idea for a moment, just consider an arbitrary idea presented by some person in the world. Is it efficient to get the world's leading physicists to apply their time to look at all these people's ideas? Isn't it more efficient for them to concentrate on peer-reviewed research papers in the journals? Now, sometimes a good idea that appeared on a forum is going to be missed. That's a shame, don't get me wrong, that is a real shame - but if all the physicists were reading forums instead of journals then hardly any new research gets done by them and that seems to be a much greater loss.
This forum is quite small, there aren't many users, who do you think is here and what do you think they can or should do?
Best Wishes.
The pursuit of the truth is the most noble inclination of the human nature.
What do you think about the presented calculations and the conclusion there is a preferred frame?
Post by: Origin on 28/04/2023 15:25:14
What do you think about the presented calculations and the conclusion there is a preferred frame?I think you need to keep an open mind and listen to the responses you got to your question. I'm sure it is very exciting to think you have discovered something that has been missed by millions of physicists. Isn't it much more likely that you have just made an error in your analysis?
Post by: Jaaanosik on 29/04/2023 16:33:50
No, I did not get my questions answered.What do you think about the presented calculations and the conclusion there is a preferred frame?I think you need to keep an open mind and listen to the responses you got to your question. I'm sure it is very exciting to think you have discovered something that has been missed by millions of physicists. Isn't it much more likely that you have just made an error in your analysis?
Could I be wrong? Sure!!!
Interesting though, Halc stopped posting when I asked him if Ω=1 makes the rest frame the preferred frame, isn't it?
Why are K'1, K'2 curvature radius' dismissed in their respective frames?
These are the questions for all physicists.
Am I wrong? No I am not wrong till the questions are answered.
Post by: Jaaanosik on 29/04/2023 16:44:05
I did in my post #32.over 90% percent of what I said is textbook stuff.I disagree with that since I see no mention of your funny trochoid analysis in the one page of book you show.
If you're going to use trochoid mathematics for the acceleration of point B, you also need to use it for the A points, but you're not doing that. None of that is in the tiny bit of textbook you mention although I imagine it's covered somewhere.
...
Here it is again for 4m radius:
(https://i.imgur.com/qt08MCn.png)
What you call 'funny trochoid analysis' is a generic motion as seen by an inertial frame and the generic equations apply for the instantaneous acceleration calculation.
Post by: Halc on 30/04/2023 00:54:32
The textbooks are clear, there are only Ω and ω.The textbook (or at least the one page you show) discusses a formulation using the proper frame of the motion, the one frame where everything is back in the same place after a rotation. It does not discuss the trochoid method at all.
The trochoid method works, but it doesn't have 4 lines (components) like you're showing. It needs to be done separately based on the path taken by the point in question (in this case, each of the A points, each of which has a different curvature. You've not computed that, but are instead attempting to mix the trochoid method for a different point with what the textbook does.
So find a textbook that discusses the trochoid method. You have a point taking a sort of helical path through space, and at any given point it indeed has a curvature and speed from which a momentary radius can be determined.
You haven't done that for any of the A points, and you did it for B only in the one frame with only X motion. Do it (compute the acceleration of B) in the frame were V=(0,1,0) instead to illustrate what is involved. Having done that, try to generalize to the curve of say A4.
The generic motion equations are used for an instantaneous acceleration calculations and they are supposed to work for any inertial observer if the relativity is true.This has nothing to do with relativity theory. The book discusses Newtonian mechanics. The mathematics of the same thing in relativity theory is completely different. What the book discusses works fine for slow speeds and accelerations like the example, but fall apart when they get large. Rotation (ω) is absolute (frame independent) in Newtonian mechanics, but is frame dependent in relativity.
Proper acceleration is a physical fact. An accelerometer at A4 can measure and print on paper the value at the moment in question, and it can only print one value. It is a logical inconsistency to have it print a different value when expressed in a different frame, but that seems to be what you are asserting.
Quote
Generic curved trajectory has two accelerations, normal and tangential.Yes. Are you taking both into account? I don't see it.
Quote
The point B is at the top of the cycloid in K'1 frame and there is only pure normal/centripetal acceleration, there is no tangential acceleration.Only because you've chosen a frame (1,0,0) where there's no tangential acceleration. Again, try (0,1,0) where there very much is tangential acceleration. Does your method work (for point B) in that frame? Do you even have a method? What is the curvature and speed in that frame?
The pursuit of the truth is the most noble inclination of the human nature.Kind of facing the wrong way to do that. You seem to be trying to beat off truth with a stick as it chases you. I mean this. It's quite apparent in all your topics.
[/quote]What do you think about the presented calculations and the conclusion there is a preferred frame?[/quote]You're confusing 'preferred frame' with 'proper frame'. To illustrate, consider 20 of your wheels going in all directions and orientations and speeds relative to each other, and from that, can you determine the perferred frame? No. Your calculations only yield the correct result when computed in the proper frame of each object (the frame K as you call it) which is different for each object. Hence no preferred frame has been demonstrated.
Interesting though, Halc stopped posting when I asked him if Ω=1 makes the rest frame the preferred frame, isn't it?The correction to your computations was posted. You choose to reject it. I have little more to contribute that isn't just repetitive. It became a troll topic after about 40 posts when it became again clear that learning wasn't a goal.
Apologies for the harsh assessment, but it's pretty glaringly obvious to me. If you disagree, then prove me wrong. It wouldn't be hard to do.
Quote
Why are K'1, K'2 curvature radius' dismissed in their respective frames?I never dismissed the curvature radius differences in various frames. But you didn't compute the curvature radius in the (0,1,0) frame, nor the radius for any of the A points in any frame at all. But if you're going to compute the acceleration with that method, you need to compute not only each curvature radius, but also the tangential acceleration along that curve. It's considerably more complicated than the method discussed in the book page.
Did not, as evidenced by the self-contradictory results. That's using an invalid mix of two methods. There would be only two (not four) components to a proper trochoid method, one for normal acceleration and one for tangential. You're not doing that. Your taking trochoid acceleration for a different point (B) than the one you're computing (the A points), and then you're adding in components that are relative to the frame of B, but not using numbers from the frame of B.If you're going to use trochoid mathematics for the acceleration of point B, you also need to use it for the A points, but you're not doing that.I did in my post #32.
Start with just figuring out B in the (0,1,0) frame. If you get that, then you can attempt the A points. Two terms for each. I cannot recommend a web page that says how to do it this way, but it can be done.
Post by: Jaaanosik on 01/05/2023 00:05:41
Halc, thanks for your post!The textbooks are clear, there are only Ω and ω.The textbook (or at least the one page you show) discusses a formulation using the proper frame of the motion, the one frame where everything is back in the same place after a rotation. It does not discuss the trochoid method at all.
The trochoid method works, but it doesn't have 4 lines (components) like you're showing. It needs to be done separately based on the path taken by the point in question (in this case, each of the A points, each of which has a different curvature. You've not computed that, but are instead attempting to mix the trochoid method for a different point with what the textbook does.
So find a textbook that discusses the trochoid method. You have a point taking a sort of helical path through space, and at any given point it indeed has a curvature and speed from which a momentary radius can be determined.
You haven't done that for any of the A points, and you did it for B only in the one frame with only X motion. Do it (compute the acceleration of B) in the frame were V=(0,1,0) instead to illustrate what is involved. Having done that, try to generalize to the curve of say A4.
This has nothing to do with relativity theory. The book discusses Newtonian mechanics.
...
It is long so I'd like to reply per parts.
Let us settle the relativity.
(https://i.imgur.com/kgOcgRW.png)
So selection of moving point B is arbitrary and acceleration at A is acceleration of B and relative acceleration between A/B.
Quote
Only because you've chosen a frame (1,0,0) where there's no tangential acceleration. Again, try (0,1,0) where there very much is tangential acceleration. Does your method work (for point B) in that frame? Do you even have a method? What is the curvature and speed in that frame?So in K'1, K'2 the point B follows cycloid motion trajectory and the acceleration analysis reflects curvature radius of those respective frames.
K'1 B acceleration is pure normal with r=4m, K'2 B acceleration is pure tangential.
My calculations account for that.
Post by: Halc on 01/05/2023 02:22:47
Halc, thanks for your post!There's an option to do it in actions, top of the list.
Quote
Let us settle the relativity.By relativity, I mean relativity theory, which has totally different equations and properties than does Newtonian physics. So for instance, if I put an accelerometer at the end of a 2770 km string and spin it at a proper rate of 1000 RPM, under Newtonian physics it will read about 2.9e8 m/s² but relativity theory says it will read about 1.14e9 m/s². Under Newtonian physics, the spin is 1000 RPM relative to any inertial frame, but the angular speed is frame dependent in relativity theory. Those differences are what I'm talking about, not the fact that speed is relative to something, which is true for both theories.
Your examples have not in any way touched on relativity theory or the equations involved with it, so any assertions about it being wrong are baseless since it has never been discussed in this topic.
Your book page at the bottom correctly says "it is important to realize that the acceleration of a particle as observed in a translating system x-y is the same as that observed in a fixed system X-Y if the moving system has a constant velocity".
You contradict this with your calculations showing non-identical accelerations as observed in different moving systems.
Quote
So selection of moving point B is arbitrary and acceleration at A is acceleration of B and relative acceleration between A/B.Yes, but you are not correctly computing the latter since they are not based on the motion of A relative to B.
As I said in my prior post, I'm mostly repeating myself, as are you. This is unproductive.
Quote
I still don't see you doing it in K'3 using frame (0,1,0). I'm challenging the validity of your method, and you seem to evade it rather than demonstrate it. What is the radius of curvature of the path of point B in that frame? What is the velocity of B in that frame? Most importantly, what is the acceleration of B in that frame, and how do you arrive at that using your method?QuoteOnly because you've chosen a frame (-1,0,0) where there's no tangential acceleration. Again, try (0,1,0) where there very much is tangential acceleration. Does your method work (for point B) in that frame? Do you even have a method? What is the curvature and speed in that frame?So in K'1, K'2 the point B follows cycloid motion trajectory and the acceleration analysis reflects curvature radius of those respective frames.
K'1 B acceleration is pure normal with r=4m, K'2 B acceleration is pure tangential.
My calculations account for that.
I don't think you have a method.
Post by: Jaaanosik on 01/05/2023 16:37:30
The K'1, K'2 calculations work fine for A1, A2, they do not contradict the rest frame K.Halc, thanks for your post!There's an option to do it in actions, top of the list.QuoteLet us settle the relativity.By relativity, I mean relativity theory, which has totally different equations and properties than does Newtonian physics. So for instance, if I put an accelerometer at the end of a 2770 km string and spin it at a proper rate of 1000 RPM, under Newtonian physics it will read about 2.9e8 m/s² but relativity theory says it will read about 1.14e9 m/s². Under Newtonian physics, the spin is 1000 RPM relative to any inertial frame, but the angular speed is frame dependent in relativity theory. Those differences are what I'm talking about, not the fact that speed is relative to something, which is true for both theories.
Your examples have not in any way touched on relativity theory or the equations involved with it, so any assertions about it being wrong are baseless since it has never been discussed in this topic.
Your book page at the bottom correctly says "it is important to realize that the acceleration of a particle as observed in a translating system x-y is the same as that observed in a fixed system X-Y if the moving system has a constant velocity".
You contradict this with your calculations showing non-identical accelerations as observed in different moving systems.
There are countless examples where this is the case.
I picked points A3, A4 for a reason, to point out 'the spin-orbit' interaction.
The point of interest is to analyze what is different for A3, A4 points when compared to A1, A2.
Quote
Here is the calculation for K'1 frame after Pi/2 time that is equivalent to your K'3.QuoteSo selection of moving point B is arbitrary and acceleration at A is acceleration of B and relative acceleration between A/B.Yes, but you are not correctly computing the latter since they are not based on the motion of A relative to B.
As I said in my prior post, I'm mostly repeating myself, as are you. This is unproductive.QuoteI still don't see you doing it in K'3 using frame (0,1,0). I'm challenging the validity of your method, and you seem to evade it rather than demonstrate it. What is the radius of curvature of the path of point B in that frame? What is the velocity of B in that frame? Most importantly, what is the acceleration of B in that frame, and how do you arrive at that using your method?QuoteOnly because you've chosen a frame (-1,0,0) where there's no tangential acceleration. Again, try (0,1,0) where there very much is tangential acceleration. Does your method work (for point B) in that frame? Do you even have a method? What is the curvature and speed in that frame?So in K'1, K'2 the point B follows cycloid motion trajectory and the acceleration analysis reflects curvature radius of those respective frames.
K'1 B acceleration is pure normal with r=4m, K'2 B acceleration is pure tangential.
My calculations account for that.
I don't think you have a method.
(https://i.imgur.com/Lijffwc.png)
All the partial calculations are in (n-t) coordinates the last line is in X,Y,Z coordinates.
Post by: Jaaanosik on 04/05/2023 13:20:23
(https://i.imgur.com/prXV9EO.png)
(https://i.imgur.com/hMVGSzV.png)
These points have Coriolis acceleration, 2Ω cross product with the relative velocity.
That's the reason different Ω generates different Coriolis acceleration.
If Ω=1 and it cannot be changed then the analysis is done only in the rest frame.
K'1, K'2 frames cannot have Ω=1.
Post by: Jaaanosik on 04/05/2023 20:32:06
(https://i.imgur.com/2ayniWH.png)
One component is vrel change of direction dθ.
The second component is change or radius.
These are frame dependent therefore only one frame can predict the correct proper acceleration.