Super bainite, a surprisingly-strong steel, is the subject of this week's Naked Scientists. We discover how it's made in the metallurgical equivalent of a pizza oven, why it makes the best bearings and how, even when it's full of holes, it also makes great armour. In the news, a nanotechnological tool to unblock blood vessels, a dust cloud that's disappeared around a nearby star and have we found the Higgs? Plus, can your cutlery affect the flavour of food?
In this episode

01:25 - Super Strong Super Bainite
Super Strong Super Bainite
with Professor Harry Bhadeshia, University of Cambridge
Ben - Steel is an enormously versatile metal and centuries of trial-and-error bucket chemistry has given us a wide range of steel alloys that are capable of performing every task that we set. So it might surprise you to hear that steel can still surprise us with previously unthought of properties. Here to tell us more about a new variety of steel, super-strong super bainite, is Professor Harry Bhadeshia who invented super bainite at Cambridge University. Harry, thank you ever so much for joining us.
Harry - It's my pleasure.
Ben - So, tell us what's so special about this new type of steel?
Harry - Well, most steels are crystalline in nature, so if you look at them in  a microscope, you'll find very fine crystals, usually of the order of a millionth of a metre in size. Now, the finer you make these crystals, the stronger the material becomes and also tougher. So, toughness is the ability of the material to absorb energy when you hit it, otherwise, the material is not safe when something impacts against it. So, the idea here was to make the crystals so incredibly fine that they're actually finer than carbon nanotubes. So that is talking about 10th of a billionth of a metre in size.
a microscope, you'll find very fine crystals, usually of the order of a millionth of a metre in size. Now, the finer you make these crystals, the stronger the material becomes and also tougher. So, toughness is the ability of the material to absorb energy when you hit it, otherwise, the material is not safe when something impacts against it. So, the idea here was to make the crystals so incredibly fine that they're actually finer than carbon nanotubes. So that is talking about 10th of a billionth of a metre in size.
Ben - And how do you actually do that? How do you go about controlling the size of these crystals?
Harry - We discovered that if we grow the crystals inside the solid steel at a low enough temperature then they will grow extremely fine. So in this case, we are heat-treating the steel at the same temperature at which you would cook pizza. The only catch is that we need to hold the steel at 200 ° C for 10 days. So it's a very long cooking process, at around 200° C.
Ben - And is it all about that heat treatment or are you adding extra alloying elements as well that give it these properties?
Harry - We have added silicon in particular to stop the growth of detrimental crystals. So, there are some crystals which are bad for toughness and one of those is iron carbide. And if you add the right amount of silicon then the formation of that ion carbide is suppressed.
Ben - So, we think of steel or at least I think of steel from a lay perspective is just being iron and carbon, but clearly, it is more complicated than that. How many different elements go into super bainite?
Harry - There's at least ten different solutes that we add. So apart from silicon, we add molybdenum because when we make the steel commercially, we can't control certain impurities, and molybdenum acts like a scavenger and gets those impurities, and therefore, stops them from doing harm to the steel. We've got chromium and manganese to stop other reactions which happen at high temperatures. So it's a very carefully designed steel.
Ben - Centuries of bucket chemistry have gone in to making better steels, but your technique has been somewhat more scientific?
Harry - Partly true. So what we do is we first start with calculations, go as far as we can, and then do the experiments to validate the calculations. If they're not correct, we go to that loop again. And that is a better way of doing it because we develop the theory at the same time as we reach our goal.
Ben - And speaking of the theory, what is it about having tiny crystals that gives it these properties? How does the crystal structure affect the final properties?
Harry - So, if we pack a very large number of crystals inside the same volume, then you are presenting a lot of boundaries between crystals to any deformation. And the finer you make the crystals, the greater the surface area between crystals in that given volume. So that makes it extremely difficult to deform. So super bainite for example has a strength in which one square metre would be able to support the weight of 2 ½ billion apples so that's what we call 2 ½ gigapascals of strength. And because the cooking process is so slow, we can make the steel in very large dimensions and very large quantities. So it's already been manufactured in thousands of tonnes.
Ben - We have spoken to people from Rolls Royce before on the show who have talked about how they make jet engine blades for example by actually just forming them from one single crystal. Now that obviously has none of these grain boundaries, but again, that performs a fantastic task for them inside the jet engine. Is it a trade-off therefore? Does having grain boundaries offer one thing and having no grain boundaries offer something else?
Harry - Grain boundaries are very good for obtaining strength at room temperature or let's say, 200 or 300° C. But as you go higher, about 500° C, there's a bit of space inside grain boundaries which is not inside the crystal. So atoms can move about very easily in the boundaries. What that means is that if you're operating a turbine blade at 1400° C, it gets longer and longer, so in that scenario, we really don't want any boundaries between crystals, and it's better to make the blade from a single crystal.
Ben - So, you have these incredibly small crystals that give you all of these huge surface area of boundary that gives you these unique phenomenal properties. How do you see super bainite really being deployed? Where do you think it's going to be most useful?
Harry - So I'll tell you both the good points and the bad points. The good points are that we can make this large in all three dimensions with an incredibly simple heat treatment. And the steel itself is quite cheap to make. There's nothing really expensive about it. So, in any application where we require a combination of strength and toughness, this is perfect. So for example for shafts, for armour and for bearings which Alan will talk about. The weakness is that because it is so strong, it cannot be welded. So, I could not make a bridge out of it for example. Large structures really need to be joined at some point, and this material cannot be welded at the moment. We are trying very hard to do research which will discover a method of joining it without disrupting the fine scale of the crystals. We haven't found it yet, but you know, this is science, right?
Ben - I get the impression from the little I do know about the way that we do join metals that actually there's at least another hour of discussion just in talking about how to join two pieces of metal together!
Harry - Absolutely.
Ben - Well, thank you ever so much, Harry. That's Professor Harry Bhadeshia from Cambridge University.

08:16 - Building Better Bearings
Building Better Bearings
with Dr. Alan Begg, SKF
Ben - New materials are always needed to perform specific jobs and even the tiniest improvement in properties can mean the difference between an engineering success and an engineering failure, or it can make a previously expensive project economically viable. We are joined now by Dr. Alan Begg from the Swedish company, SKF. Now Alan, presumably, you rely on these sorts of step improvements all the time to make projects better, to make new products, and to remain competitive.
Alan - Absolutely. SKF is the world's largest bearings company. We've been established for over 100 years now. We were established on the back of an innovation when our founder invented what's called the self-aligning ball bearing, and SKF has led all of the developments, or most of the big developments, in the various industry ever since. You use bearings from the tiniest things that go round to the very biggest. Dental drills or disc drives in computers have bearings, right up to windmills, which I guess are topical at the moment. I think our latest bearings for the new big windmills that are being developed are nearly 4 meters in diameter.
disc drives in computers have bearings, right up to windmills, which I guess are topical at the moment. I think our latest bearings for the new big windmills that are being developed are nearly 4 meters in diameter.
Ben - Wow! When I think of bearings, I think of the constituents of my bike that I occasionally have to get replaced, I have to grease up. And those seem to basically just be tiny steel balls. What properties do you actually need in a metal that's going into a bearing?
Alan - Well, the steel balls are how most people think of bearings. And although SKF's name is associated with steel balls, we don't actually make our own steel balls anymore. They're pretty much commodity materials. The clever bits of a bearing are actually the two rings - the inner and the outer race ways that the balls rotate in. Basically, any bearing is a set of rolling elements separating those two inner and outer rings rotating to allow the inner and outer rings to rotate as freely as possible. The raceways, the inner and outer rings, the surface where the rolling element touches the raceway, can be incredibly highly loaded.
I was a metallurgist myself once, I actually studied metallurgy here at Cambridge and I remember being told then that steel was getting pretty close to its theoretical strength. The theoretical strength of steel, if you calculate it just in terms of the strength of a bond is about 20 gigapascals and I was told when I was studying material science here in Cambridge that we were getting to about 10% of that strength. As long as you did it in thin steel wire ropes, you could get to about 2 gigapascals. I now look at bearings and for bearings a 2 gigapascal load is nothing! In fact, the compressive stress that's put on a bearing at the point of contact where a ball touches the ring, routinely, it's about 4 gigapascals and at extreme conditions, it can be getting close to 8 gigapascals. Not for very long times, but it will stand it for a little while.
Ben - And so, what's changed? Why has the future that we saw a few years ago turned out so differently?
Alan - Well, people like Harry have been developing wonderful new grades of steel. I'd really like to give credit to Harry because when I joined SKF, about 5 years ago, I was quite surprised how much we relied on steel, and how little work was going on across the world to really generate new performances in steel. That's one reason why I really wanted to setup a major cooperation with Cambridge University and with Harry. SKF have setup what we call a University Technology Centre in Cambridge to exploit, amongst other things, super bainitic steels, but to also build our fundamental understanding of what really happens within a steel at that critical point of contact.
 And we have other university technology centres, another one in the UK with Imperial College in London on what we call tribology. This is the study of the point of contact, the friction, wear and lubrication at that point of contact. We have some university centres in Sweden as well, right up in the north of Sweden, in Lulea on condition monitoring because we provide sensors and things with our more expensive bearings to actually tell you what's going on within them and start predicting potential problems that are going to arise either within the bearing or in the rotating equipment around the bearing. We've always described the bearing as being at the heart of any rotating plant. By adding condition monitoring you can think of it as the brain as well.
And we have other university technology centres, another one in the UK with Imperial College in London on what we call tribology. This is the study of the point of contact, the friction, wear and lubrication at that point of contact. We have some university centres in Sweden as well, right up in the north of Sweden, in Lulea on condition monitoring because we provide sensors and things with our more expensive bearings to actually tell you what's going on within them and start predicting potential problems that are going to arise either within the bearing or in the rotating equipment around the bearing. We've always described the bearing as being at the heart of any rotating plant. By adding condition monitoring you can think of it as the brain as well.
Ben - And going back to today's topic, super bainite, what is it about super bainite? What is it about these properties that makes it so attractive for you?
Alan - What we need in a steel is what's called fatigue resistance. A bearing, that rolling element rolls round and round, and round. So if you imagine any element on the ring underneath that point of contact, it's continually getting stressed and then relaxed, and stressed and relaxed over and over again. And when you do that to a piece of metal, you get what's called fatigue damage. Under this compressive load, you get what's called rolling contact fatigue damage, and that's quite a difficult thing to prevent happening. That's the way the bearing's loaded.
We've looked at many, many different microstructures created in many, many different ways and super bainite seems to us to be the first real step change in thinking in steel for a very long time. Will it give us all we want? I don't know. We're still very much at the stages of examining it. Are there still some interesting challenges? Yes, I think there are. One of them is that the structure has some slightly unstable nature about it, that some of the high temperature form of steel is left in between those very, very fine nanoscale structural parts and if that transforms during loading, it actually leads to a slight increase in volume. Now the intriguing bit is, first of all, will it happen? But if it does happen, could this growth, could this expansion, actually compensate for wear? Could we make a material that, as it wears down, it grows up and compensates in some ways for the wear? So, there's all sorts of intriguing science still to be done in super bainite. But as I say, as a material, it's got the right kind of hardness, strength, and toughness that we're looking for in a bearing steel. And so, we're very interested to see if we can exploit its properties to make stronger, better bearings for our vessel.
15:13 - CF and pH – Lung Acidity in Cystic Fibrosis Increases Infection
CF and pH – Lung Acidity in Cystic Fibrosis Increases Infection
Sufferers of Cystic Fibrosis, or CF, have lower pH in their airways and this impairs their ability to kill bacteria, leading to increased infections, inflammation and ultimately damage to lung tissue.
CF is a genetic condition caused by mutations in the Cystic Fibrosis Transmembrane conductance Regulator, or CFTR, gene. The CFTR protein regulates the movement of ions across membranes, including the lining of the lungs, and its failure leads to symptoms such as the build up of thick, viscous mucus. People with CF are especially vulnerable to lung infections, and these infections are ultimately the main cause of illness and death in CF patients, but until now it's not been clear how CF impaired the ability of the immune system to tackle infection.
 Writing in Nature, Joseph Zabner and colleagues at the University of Iowa immobilised Staphylococcus aureus bacteria on solid grids and placed these on the lung surface of both healthy and CF pigs. Even a brief exposure to healthy lung tissue killed the bacteria, while only half as many were killed in the CF lungs. This pattern held up in vitro and against other bacteria; consistently, Airway Surface Liquid, or ASL, from CF pigs killed fewer bacteria than from their healthy littermates.
Writing in Nature, Joseph Zabner and colleagues at the University of Iowa immobilised Staphylococcus aureus bacteria on solid grids and placed these on the lung surface of both healthy and CF pigs. Even a brief exposure to healthy lung tissue killed the bacteria, while only half as many were killed in the CF lungs. This pattern held up in vitro and against other bacteria; consistently, Airway Surface Liquid, or ASL, from CF pigs killed fewer bacteria than from their healthy littermates.
This showed that ASL itself rapidly kills bacteria, and that this effect was impaired in CF. There were no obvious differences in the abundance of antimicrobial proteins between CF and non-CF, so the researchers concluded it must have been another chemical factor. As the CFTR protein is linked with secretion of hydrogen carbonate, or HCO3-, an ion important in pH buffering, they decided to investigate the effect of pH. They found that both in vivo and in vitro, CF lung fluids showed a lower pH. Raising the pH of CF lung fluids restored the ability to kill bacteria.
This simple, elegant study suggests that correcting lung fluid pH could prevent infection taking hold in CF lungs, and could be achieved by something as simple as a bicarbonate aerosol.

18:38 - Nanotherapeutics: tiny particles reach places other drugs can't access
Nanotherapeutics: tiny particles reach places other drugs can't access
A nanoscale solution to unclogging blocked blood vessels has been revealed by scientists this week.
Dubbed SANTS - shear activated nanotherapeutics - these particles, which are roughly a thousandth of a millimetre across or about same size as a blood platelet, are made by  drying a fine spray of the chemical polylactic co glycolic acid (PLGA). This results in loosely-bound aggregates of much tinier particles that attract and bind one another hydrophobically.
drying a fine spray of the chemical polylactic co glycolic acid (PLGA). This results in loosely-bound aggregates of much tinier particles that attract and bind one another hydrophobically.
Critically, these aggregates remain bound together when flowing around the bloodstream under normal conditions. But when they pass through areas of high shear stress or turbulence, caused for instance by a blood clot that has narrowed a blood vessel, the particles break up, dispensing as they do so any chemical cargo that has been coupled to them.
In initial tests using an artificial blood vessel containing a narrowed region simulating a 90% obstruction, Donald Ingber and his team at Harvard showed that, in the region of the blockage where the shear forces on fluid flowing past were more than 10 times normal, this provoked infused SANTs to disaggregate in the region of the obstruction.
Next the team prepared SANT particles that were each loaded with 500,000 molecules of a clot-dissolving protein called tPA (tissue plasminogen activator). These SANTs were able to clear blood clots from abdominal vessels and even dissolve clots obstructing the arteries of the lungs (known as pulmonary emboli) in experimental mice.
Critically, none of the treated animals developed bleeding from any other sites in the body, proving that deployment of the clot-busting treatment was being selectively restricted to those regions where the agent was needed.
This is a significant improvement on current anti-thrombolytic therapies for heart attacks and strokes where clot-dissolving drugs are injected intravenously and can hence affect every tissue, potentially precipitating haemorrhages at other sites including in the brain or intestines.
The next step will be to test the technique on humans. But, as the team point out in their paper in Science this week, before this can occur, a safer way to couple the anti-clot chemicals to the nanoparticles will need to be found. The system they have tested uses a form of molecular velcro called streptavidin-biotin, but this can trigger an immune response, potentially limiting the use of the therapy.

23:16 - The Dusty Disc Disappearance
The Dusty Disc Disappearance
A huge, hot dusty disc around a Sun-like star seems to have vanished before our very eyes, and its disappearance cannot be explained by any current scientific theory.
The star TYC 8241 2652 1 has been observed by a number of telescopes, and a bright infra-red glow indicated the presence of a large amount of warm dust absorbing visible light from the star and re-emitting it in the infra-red range.
Carl Melis and colleagues at the University of California, San Diego report in Nature that this dust seemed to be the result of collisions of rocky objects and fell in the region analogous to where rocky planets formed in our solar system. Estimation of the size of dust grains hinted that this could be a system undergoing an active stage of terrestrial planet formation. This made it an ideal candidate for future observation; as calculation of likely grain size suggested our theories of planetary formation suggest that rocky planets like the Earth will eventually form from these discs of dust and ice.
However, since 2008, the infra-red emission from this star has reduced by a factor of about 30, suggesting that the star is now only host to a meagre amount of far cooler dust. This is an unprecedented observation, changes like this have never been seen or even predicted before, so what could have caused it?
 No major changes have occurred in the star in this time, so it's unlikely that a violent stellar event blew the dust away. Models of planet formation predict the loss of dust over at least many thousands of years, as the gravitational field of newly formed planets disturb the dust cloud.
No major changes have occurred in the star in this time, so it's unlikely that a violent stellar event blew the dust away. Models of planet formation predict the loss of dust over at least many thousands of years, as the gravitational field of newly formed planets disturb the dust cloud.
Melis argues that only two hypotheses could fit the results. They are:
- The collisional avalanche hypothesis, where dust grains become gradually smaller through collisions, until they're below a certain threshold and are blown out of the system by radiation pressure from the star.
- Runaway accretion, where gas in the cloud places aerodynamic drag on the dust, causing it to fall in to the star.
However both ideas have problems, so the jury is still out.
Even though we lack a clear explanation for what has happened in this system, it is a unique observation and certain to push our understanding of how planets like the Earth first form.

25:59 - Seeing the Supersonic - A new way to look at Explosives
Seeing the Supersonic - A new way to look at Explosives
with Profesor Chris Bishop, Microsoft Research Cambridge
Chris - Well, also this week, a unique and explosive demonstration took place at Cambridge University. Explosives play a huge role in our lives from mining the materials that make computers and cars through to excavating tunnels and even controlling avalanches, and of course, lighting up the skies for nice firework displays. Professor Chris Bishop, Chief Research Scientist at Microsoft Research in Cambridge, wanted to highlight the science and technology in explosives rather than just gratuitously blowing things up! That included both humble gun powder and also modern high explosives, and he found a clever new way to show them all off in a talk that he gave earlier this week...
Chris B. - Black powder is really just a mixture. It's a mixture of charcoal, sulphur and so-called saltpetre or potassium nitrate, and it works because the saltpetre, the potassium nitrate acts at a very concentrated source of oxygen. So the carbon in the charcoal and the sulphur, instead of burning in the oxygen from the air, they burn and they built in oxygen in the potassium nitrate and so, it's a much more concentrated form of oxygen, therefore, a much more concentrated and intense combustion.
saltpetre, the potassium nitrate acts at a very concentrated source of oxygen. So the carbon in the charcoal and the sulphur, instead of burning in the oxygen from the air, they burn and they built in oxygen in the potassium nitrate and so, it's a much more concentrated form of oxygen, therefore, a much more concentrated and intense combustion.
Chris - So if I light it, what happens? Does it immediately go bang?
Chris B. - Not quite. What happens is that the ingredients first of all have to melt so that the molecules can come into contact with each other. The potassium nitrate has to start to decompose. It needs a certain amount of heat to get it going and then the chemical reactions can take place. They are essentially reactions of burning so the carbon in the charcoal will burn with oxygen from the potassium nitrate to make carbon dioxide and release energy for example. And we can try it here if you like. I've got 1.5 grams of a good quality commercially gun powder and we'll see what happens when I just light a pile of this gun powder in the open.
- Pffffft! -
Chris - A lot of smoke, but it wasn't a bang.
Chris B. - No bang. So what we have there was a very, very rapid burning. The technical term we give that is deflagration, but it just means burning. What's happening is, imagine a trail of gun powder and setting fire to one end. As the gun powder at one end burns, it generates heat and that heat raises the temperature of the bit of gun powder next to it in the trail. When that gets hot enough, that in turn will combust. And so, it's a process of propagation involving the transfer of heat. It's a relatively slow process. In that case, there's no explosion at all. If we actually want to get a bang, if we want to get a proper explosion, we need to speed things up.
Chris - So when Guy Fawkes shoved tons of gun powder under the houses of parliament - hoping to blow it up - would that not have worked then because it was just a pile of gun powder, rather like you had there.
Chris B. - Well of course it was in a cellar and surrounded by very thick stone walls. So it would've been very well confined. So I think there's little doubt that it would've resulted in an enormous explosion and a complete destruction of the House of Lords, yes.
Chris - So is that how explosives involving gun powder actually work then, you confine the explosion?
Chris B. - That's right. So if you're listening to a fireworks display, and you're listening to all the bangs, it will be gun powder or another type of low explosive that's been confined in order to produce the bang. Again, we can illustrate that here because I've got another sample. It's again 1.5 grams of gun powder. It's exactly the same type as before but this time, I put it into a cardboard tube and bound it up very tightly with tape. So it's very strongly confined and what we'll do is we'll set this off using a little electrical igniter that's buried inside the gun powder.
Chris - I'll should put on some ear defenders.
Chris B. - Okay, ready? Here we go.
- BANG! -
Chris - Okay, my ear is ringing even though I had the ear defenders on. That was exactly the same amount of gun powder we lit that went puff before, but that's the power of confinement. You get that huge bang.
Chris B. - That's right. That's dramatically different, but it's still a very rapid burning. So what's happening is that as the gun powder starts to burn, it releases energy in the form of heat, but that heat is now trapped. It can't just escape. And so, the temperature rises and chemical reactions go faster at higher temperature. So, as the temperature increases, the rate of reaction increases, and so, the rate of heat production increases, this in turn raises the temperature. We have a positive feedback loop leading to a runaway reaction which resulted this explosion. For many years, perhaps a thousand years, that was really the only kind of explosive that people had. And then some time around the middle of the 19th century, people began to discover new kinds of explosives, so-called high explosives.
Chris - Fundamentally, why are they different to gun powder?
Chris B. - The key difference is the way in which they are initiated. So gun 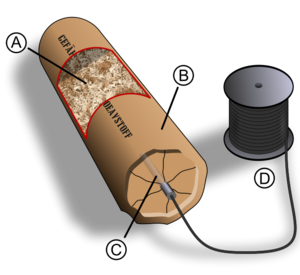 powder undergoes this very rapid burning. High explosives - something like nitro-glycerine or TNT - decomposes by a process called detonation which is a very different physical process and it's very much faster, and very much more powerful, because the oxygen is "built in" to the same molecule. So in a molecule of let's say, nitro-glycerine, you have the carbon and the hydrogen. We also have the oxygen and the nitrogen. That's the most perfect mix you can have between the fuel and oxygen. The carbon can combine very readily with the oxygen to make carbon dioxide. The hydrogen can combine with oxygen to make water. The nitrogen is left over. Nitrogen occurs a lot of explosives. It's very important because nitrogen gas in the air, consists of molecules containing two atoms joined together by one of the strongest bonds in chemistry. So if two atoms of nitrogen get together to make a molecule, they release a lot of energy. That's one of the reasons why high explosives release so much energy.
powder undergoes this very rapid burning. High explosives - something like nitro-glycerine or TNT - decomposes by a process called detonation which is a very different physical process and it's very much faster, and very much more powerful, because the oxygen is "built in" to the same molecule. So in a molecule of let's say, nitro-glycerine, you have the carbon and the hydrogen. We also have the oxygen and the nitrogen. That's the most perfect mix you can have between the fuel and oxygen. The carbon can combine very readily with the oxygen to make carbon dioxide. The hydrogen can combine with oxygen to make water. The nitrogen is left over. Nitrogen occurs a lot of explosives. It's very important because nitrogen gas in the air, consists of molecules containing two atoms joined together by one of the strongest bonds in chemistry. So if two atoms of nitrogen get together to make a molecule, they release a lot of energy. That's one of the reasons why high explosives release so much energy.
Chris - But when we want to make it blow up, what do you need to do for that?
Chris B. - So what we need to do then is to send in a very fast shockwave in order to get the explosive to detonate. So, a detonation is where a shockwave is traveling through the explosive, very much faster than the speed of sound. So this modern high explosive would detonate at the speed of about 8,000 metres per second.
Chris - Gosh! So that shockwave is putting energy into the chemical bonds in the mixture, breaking some of them and making others recombine which then makes a bigger shockwave which then goes on to the next bit of the molecule, and you get a sort of explosive domino effect for want of a better expression.
Chris B. - Yes, exactly right. It's the energy released by the high explosive which sustains that shockwave. If you sent a supersonic shockwave into a block of material, it would rapidly slow down to the speed of sound. But if the materials are high explosives, because it's detonating or releasing energy, that energy just behind the shock front is sustaining the shock front and keeping it going at that supersonic speed. So, one of the things I really want to do in the lecture is to try to give people a sort of visceral feeling for just how fast the detonation occurs. So I came up with the idea of using something called shock tubing. So I've got some shock tubing here and it looks just like a piece of yellow plastic tubing, 3 mm across. It's got a 1 mm diameter hole down in the middle and inside, it contains a very light dusting of high explosive called HMX. This is one of the most powerful explosives known and what I can do now is to demonstrate a shockwave traveling down the tube.
Chris - This little piece of plastic tube is about 20 cm. What are you going to use to detonate it?
Chris B. - What I'm doing is plugging it into an initiator which is essentially an electrical device. It has a couple of buttons. I press the first button which will charge up a capacitor. When I press the second button, it would produce a spark and that's enough to initiate the shockwave.
- BANG!!! -
Chris - I certainly didn't miss that. And you could see the flash go down the tube.
Chris B. - That's right. But of course, at such a high speed, it appears to be essentially instantaneous. So, what we'll be doing in the lecture is to use half a kilometre of shock tubing and this is being wound as you see around the walls of the lecture theatre, so we'll go around the audience 4 or 5 times and then what we're doing is to initiate one end of the shock tubing and about a quarter of a second later, the shockwave will arrive at the other end. What I'm hoping is the audience will actually be able to perceive the delay between the start of the shockwave and the end of the shockwave, and might even be able to see this pulse of light racing around their heads several times.
Chris - Has anyone ever tried to blow up a lecture theatre in this way in the past?
Chris B. - I'm certainly hoping not to blow up the lecture theatre! But I think it's the first time, as far as I know, that somebody has tried to use this sort of method to illustrate the speed of detonation as a live demonstration in a lecture theatre.
Chris - And I'm pleased to say, it definitely worked. People reported seeing the explosion whirl around their heads. So well done to Professor Chris Bishop with a first of its kind demonstration, surrounded the audience with high explosives.

34:10 - Have we found the Higgs Boson?
Have we found the Higgs Boson?
with Rolf Heur, CERN; Joe Incandela, CMS Experiment; Jordan Nash, Imperial College London; Emily Nurse, UCL
This week saw scientists at CERN announce the discovery of a Higgs' Boson-like particle at the Large Hadron Collider, or LHC.
The existence of the Higgs' Boson has long been part of the so-called standard model of particle physics but until now its existence wasn't confirmed.
model of particle physics but until now its existence wasn't confirmed.
CERN Director General Rolf Heur...
Rolf - We have discovered a new particle. A Boson. Most probably a Higgs' Boson, but we have to find out which kind of Higgs' Boson this is, what are its properties, and where do they point to. But at least, we know now that we can soon close part of the chapter of the standard model. We have now found the last missing cornerstone of it. It's the beginning of a long journey to investigate all their properties.
The discovery answers a long-standing question regarding why some of the fundamental particles in the Universe, like protons and neutrons, and the quarks, leptons and bosons that make them up, actually have mass. The Boson was detected by the CMS and ATLAS experiments.
Professor Joe Incandela is from the CMS experiment...
Joe - This boson is a very profound thing that we've found. Okay, this is not like other ordinary particles. We're reaching into the fabric of the universe, at a level we've never done before, and we're on the frontier now. We're on the edge of a new exploration.
Without the presence of Higgs' bosons located within the Higgs' field which permeates space, sub-atomic particles, such as quarks and leptons, would simply move in all directions at great speed rather than clump together to form matter.
In their search, scientists collided billions of protons every second to release large amounts of energy within which the elusive Higgs' boson could form. Only a small percentage of these collisions lead to the formation of these bosons which then decay rapidly into photons. By studying these photons the CERN scientists have been able to deduce the presence of a new fundamental particle.
Professor Jordan Nash, Head of High Energy Physics at Imperial College London explains...
Jordan - So, the two cleanest ways in which we've seen it and which are the most statistical significance are the events where it produces just two very high energy photons. So these are just two particles of light which smash into our detector very cleanly, and the Higgs' Boson always producing from with exactly its mass. So, by looking at these very, very clean signatures, we can spot it. It's very, very indeed to have such a clean signature, but it's one when you get it, you have the quite high certainty that you've actually produced a real particle.
 The teams detected particles with energy levels indicating a mass of 125-126 GeV , or 133 times heavier than a proton.
The teams detected particles with energy levels indicating a mass of 125-126 GeV , or 133 times heavier than a proton.
The findings build on preliminary results hinting at the presence of a Higgs-like particle that were announced back in December 2011, but now the CERN teams are more than 99.99994% certain of their finding, a level known as 5 sigma.
Jordan - 5 Sigma is a measurement of how statistically confident we are in our measurement being consistent with a signal as opposed to a background. And so, sigma is a measurement of the relative confidence and it comes from a probability distribution where we can have 1 sigma where you have about 1/3 chance of having gotten a computer signal with a background, 3 sigma says you have about 1 part in a thousand chance of doing that, and 5 sigma says you have less than 1 part of a million confusing a signal with background.
This confirmation would revolutionise the world of fundamental physics as well as our own. Dr. Emily Nurse from University College London is part of the Atlas project.
Emily - It's a very fundamental finding for our understanding of the universe. It's very difficult for us to say what it could possibly lead to. All we can say is that we know that our modern world has completely relied on the previous generations doing fundamental research. For example, computers, television, all the sort of medical equipment that we use - MRI scans - all of these things, they all come from understanding the universe better at a fundamental level and that just eventually then leads on to the technology as you trickle down the line.
Confirming the Higgs Boson's existence will also help scientists recreate what must have happened one ten billionth of a second after the big bang in which mass-less particles gained their mass from the Higgs field to form atoms, ultimately leading to the Universe we see today.

39:34 - Nanomaterials in our Environment - Planet Earth Online
Nanomaterials in our Environment - Planet Earth Online
with Teresa Fernandes and Helena Johnston, Heriott-Watt University
Ben - Nanotechnology promises to make smelly socks a thing of the past and we've already heard today how it could revolutionise medicine and the drugs industry. But what are the environmental dangers of these tiny particles. They're a fraction the size of a human hair, so could they have an impact on health or on the environment? A joint research project between the UK and the United States has been setup to analyse the potential risks of nano materials. One of the studies is being led by Teresa Fernandes at Heriott-Watt University in Edinburgh. Planet Earth podcast presenter Richard Hollingham went to visit her in her lab.
Teresa - We have here a range of projects looking at hazards, so we keep some organisms, very, very small organisms. We keep some primary producers, some algae and microalgae and single cell organisms, and we keep the water flea, for example, and some worms, some aquatic worms.
the water flea, for example, and some worms, some aquatic worms.
Richard - Can we have a look at some?
Teresa - Sure.
Richard - Well these look like just large freezers really, food freezers, fridge freezers.
Teresa - We could merely walk in to these ones.
Richard - So you've got these beakers, a couple of litres of beakers with slightly greenish water and these little water fleas skimming around. And then in there, you've also put some nano particles, nanomaterials to see what happens.
Teresa - If they indicate that there are reasons to be concerned, for example, there's mortality or reduced reproduction, or other end points I'm looking at, then there's a concern and if these effects happen at low concentration, there's a concern that there might be a reason to prevent, or have controls in use of these chemicals.
Richard - Teresa, while you're looking at the environmental impact of these nanomaterials, I'm also with Helena Johnston and you're looking at the impact on human health?
Helena - So, in order to do that, we can either look at the effect on cells cultured in vitro or we can look at the effects within animals in vivo.
Richard - So when you say in vitro, you mean in the test tube?
Helena - Yes, so in a cultured condition in a test tube. So, what we generally do is we take cells isolated from different parts of the body. So, you might get exposed via inhalation - so the lung would be a target; via digestion - so we have the gut, or through exposure via the skin. Once the nano particle is exposed to these different exposure sites, they can access the blood because of their small size and then travel throughout the body, so the liver is a primary target. We also look at the kidneys, the cardiovascular system. The list is endless.
Richard - Teresa has chambers full of water fleas and the like. You have some human cells.
Helena - Yeah. So the cells need to be cultured at 37 ° C because that's what you would have.
Richard - Our body temperature.
Helena - Yeah, exactly, body temperature. They need a supply of carbon dioxide and oxygen and they need a medium which gives them all the nutrients they need to grow in these artificial conditions.
Richard - So, open the cabinet up.
Helena - So we've got a variety of different cell types in here so, for example, this is an epithelial cell, so it's found within the lining of the lung.
 Richard - It just looks like a clear liquid or a slightly opaque liquid.
Richard - It just looks like a clear liquid or a slightly opaque liquid.
Helena - If you look at the back of the dish, you can see the cells growing, so all these little islands, if you like, are the cells...
Richard - So they're the same cells that we have in our lungs?
Helena - Yes, so these have been isolated, I think, from a tumour so these cells will grow indefinitely in culture. If you take them from a human, they will only divide a certain number of times and it limits the amount of times you can use these cells.
Richard - You've got some darker ones in here as well.
Helena - So these are macrophage cells. So an immune cell within the body, so they are responsible for clearing foreign materials. Again, you can see them growing on the back of the dish and whereas these epithelial cells will all grow together, these ones are isolated.
Richard - And when you're looking at these, again, you're looking for the impact of nano materials on them?
Helena - Yes, so the types of toxicity tests we do, we'll administer nano particles and see if the cells die, so they're having a cytotoxic effect. Do they elicit an inflammation, oxidative stress? So these are all common mechanisms that we know nano particles can act, and it allows us to compare the toxicity of different types of nano particles and see if they elicit a similar toxicity, or some are more potent than others.
Richard - And Teresa, doesn't this come to the nub of this that these things are already out there. Shouldn't maybe this work have been done ten years ago when these kinds of products were being developed?
Teresa - Industry can develop very fast and the research and evidence needs to take its time because you don't want necessarily to prevent an area of industry that has great promise for society. So, it's a question of getting the pace right, you know, speed up the research, speed up the ability to translate results from research to the regulatory process.

44:44 - Super-Strong Steel Armour
Super-Strong Steel Armour
with Professor Peter Brown, DSTL
Ben - Another potential application for a very strong metal is in armour, protecting people and vehicles from threats like bullets and bombs. At the Defence Science and Technology and Laboratory or DSTL in Porton Down, researchers including Professor Peter Brown work on finding the right balance of material properties for the perfect armour.
Peter - People have been looking for good armours for centuries and the trouble with armour is that as soon as you create a good one, somebody creates a bigger, better weapon to defeat it. So there's no end point you get here and go, "aha! That's the perfect armour." The other thing I always find quite intimidating about armour is you're up against Leonardo da Vinci because he invented the bullet. In terms of opposition, a da Vinci design is not easy to defeat. He's been dead 500 years and is still causing trouble. And because the rules keep changing, as soon as you feel as though you've got a grasp on what you might need for an armour, the threat changes and all those rules go out the window.
Generally speaking, it should be hard. We find the best high performance armour steels are also hard and the very, very best armours, those that provide the  highest levels of protection, are ceramics. They're unbelievably hard. But you would then have thought that something like toughness is a good thing. If you're going to give your armour a whacking great clap from a fast moving projectile, something that's tough, common sense would tell you, it is a good idea. But you look at ceramics they are as brittle as anything. If you drop a ceramic plate, it will shatter. So, common sense would tell you toughness is a good thing. So you start using common sense to help you out in armour design and you would probably come a cropper quite quickly.
highest levels of protection, are ceramics. They're unbelievably hard. But you would then have thought that something like toughness is a good thing. If you're going to give your armour a whacking great clap from a fast moving projectile, something that's tough, common sense would tell you, it is a good idea. But you look at ceramics they are as brittle as anything. If you drop a ceramic plate, it will shatter. So, common sense would tell you toughness is a good thing. So you start using common sense to help you out in armour design and you would probably come a cropper quite quickly.
Ben - I assume they can't just be a one-size fits all armour as well, if you are putting something on the outside of an armoured vehicle, that must be very different from the body armour that a soldier would wear.
Peter - That's the trouble. An armour that's good for one threat, say, armour piercing 762 ammunition, that solution probably won't work for your improvised explosive devices. So, not only is the armour properties dependent on a whole range of properties, it's also dependent on what the threat coming in is as well. That gets you to the point of trying to understand what happens at the ballistic event as the threat and the projectile, whatever it might be, hits your armour, whatever that might be. That moment of impact is an unbelievably violent event, any sensor you're putting there, by definition, it's destroyed as the bullet hits it, so it's really very difficult event to get to.
We're getting closer and closer with modern characterisation techniques, but we're not there yet. Until we actually understand the ballistic event itself, I think we're going to struggle to design armours in the sense that buildings are designed. That's thoroughly understood and if you design a structure, or a building, and the computer says "yes" you don't build a model you just build the building! Materials modelling is not at that stage yet.
Ben - How do you test the material? Presumably, you are just simulating these impacts by actually firing projectiles at a block of material.
Peter - Yup! Absolutely right. There's no substitute for putting it on the range and shooting at it because at the end of the day, you're asking people to put their lives on this technology.
Ben - So how did you come to be testing super bainite as a potential armour?
Peter - Well, it's a steel. That's a good start. The thing about steel as general comment is that it's often the solution to several questions in one material, without that much change in its compositional processing. So in terms of how well super bainite performs, bearing in mind that most things have no useful usable ballistic properties, super bainite is right out there with the very best armour steels have ever been invented. I think to be honest, armour steels for the foreseeable future are probably at their limit of ballistic performance. But yeah, super bainite is no better than the best, but as good as the very best. And trust me, that's saying something.
Ben - So how do you now see this being deployed? Is this going into body armour or is this going to line the next generation of armoured cars? Where do you see super bainite turning up?
Peter - The principal application will be for the protection of land vehicles - armoured fighting vehicles that go in the battlefield, through to diplomatic limousines. It has commercial uses as well. You can use it for steel toe caps and hacksaw blades. You can keep producing super bainite for non-defence applications day in and day out, and you can sell as much of that stuff as you can make. And then when there's a defence requirement, you just put in an order. The standard super bainite composition is slightly tweaked for defence applications. And that's where partnering with an industrial company has proved very useful. Not only are they're prepared to make the alloy, they may have to prepare to make it in a range of different product types. You can buy in the solid plate or you can buy as perforated plate which has an array of holes in it that reduce the weight and increases the ballistic performance - although traditionally putting holes in the armour is the enemy's job. It turns out that if you do it right, it's now our job.
Ben - Why would putting holes in armour make it better?
Peter - Yes, so if you're feeling confused at this point, join the rest of the world. That is an entirely rational and common-sense based feeling, but I've warned about this common sense earlier on. In fact, we're not putting holes into the armour, we're putting in edges. If you drill out half the steel and replace it with holes or fresh air, the bullet will always land near an edge, and the material will fail in an uneven way and cause the bullet to topple over, and it stops becoming a fast moving sharpened projectile pointed in the right direction and turns into a blunt toppling fragment. It still has a lot of energy, but at least a sharp pointed bit isn't heading in your direction anymore.
We've got means of energy absorption and that toppling mechanism is a way of defeating the sharpened projectile concept that da Vinci originally came up. The thing about holes is, if they're too big, then all the bullets just go through the holes. So, there's a ratio of hole size to the threat size and if you've got a big threat, you need bigger holes. But that means that the smaller threats, which are still very dangerous, can get through. So, you have to move away from the circular hole to a slot that's quite narrow, but it still has the same amount of edge length. That slotted perforated design is the one that we are probably going to go forward with and commercially exploit fairly shortly.
Ben - Professor Peter Brown, explaining why you should throw common sense out of the window and trust that holey super bainite will make good armour.
What is the crystal structure of super bainite?
Harry - There's actually two kinds of crystals. One in which the atoms are arranged at the corners of a cube with a single atom in the centre of the cube, so we call that body-centred cubic and the other one where you still have the atoms at the corners of a cube, but also at the centres of their faces, and that's a face-centred cubic crystal structure.
Ben - So that would be like looking at a die where every surface just has a one. So it's impossible to roll a 6 because they're all just ones.
Harry - Correct.
Ben - And what is it about those structures that give them their properties?
Harry - The body-centred one is very strong, but is not as tough as the face-centred cubic. So if you combine them, then you have the ability to absorb energy as well as be strong.
Ben - And so, what is it that actually causes these structures to form when you've got it in your pizza oven for however long?
Harry - First, we go to 1,000 degrees centigrade where everything is face-centred cubic and at 200 degrees centigrade, the body-centred cubic form is favoured so it grows inside the face-centred cubic form.
How environmentally friendly is this new type of steel?
Alan - The immediate reaction from all our commercial people was, "Oh my goodness! That's never going to work. We can't heat things up in a pizza oven - or in a furnace for 2 weeks!" We do do some extended heat treatments, but most of our heat treatments would be less than a day. But Harry's point of, you do all this at pizza oven temperatures is an interesting one. Normally, heat treatment is much higher temperatures than that and both the cost of a pizza oven is relatively low, and the heat loss at that temperature is relatively low, so although you're holding things for a long period of time, the energy loss could actually be a lot less.
Ben - So obviously, it needs quite a long period in order for that structure to evolve, but because it's so much lower temperature, it's altogether a more efficient process.
Alan - It could be, yes.

54:33 - Does metallic cutlery affect perception of food taste?
Does metallic cutlery affect perception of food taste?
We put this to Professor Mark Miadovnich, from University College London...
Mark: - I've got some cereal here and I'm eating it with a silver spoon. I wasn't born with a silver spoon in my mouth, but I've since acquired some. There is a slight taste from the silver, as I expected because we actually did some experiments, making spoons of different materials- gold, silver, tin, copper, zinc, and stainless steel of course. We did blind taste tests with just the spoon alone and found that people are very sensitive to the different tastes of different metals. In fact, they can distinguish between them very clearly. They find them to be, to a greater or lesser extent, bitter, metallic, unpleasant is another adjective people use for some of these metallic tastes. And that, we found out in the end was due to something called the electrode potential of the metal. So its ability to react in the mouth and produce ions of a particular type - so in the case of a copper spoon, copper ions, and in the case of silver, silver ions. So, the least reactive metals are the ones we expect to taste least, and that's broadly what we found.
Hannah - So, metals produce ions in your mouth and the more reactive the metal, the stronger the taste produced. The alloy stainless steel actually produces the mildest taste. But do some foods taste better with different materials? Professor Zoe Laughlin from University College London led blind taste tests to find out.
Zoe - Specifically, for something like a boiled egg for example where the sulphur really reacts, a material like silver is really a bad idea because it tastes really foul, whereas gold is quite delicious. And then when it comes to sweet things, we actually found the strong taste of the copper and zinc made the sweetness of the food even stronger.
Hannah - And beyond chemistry, what else can alter your perception of taste? Back to Mark Miadovnich.
Mark - The size of the spoon, the shape of the spoon, the thermal conductivity, in this case it's conducting heat away from my tongue very quickly, so it's cool. If I start using a plastic spoon now, we're into a whole different ball game. And this is where this example of thinking about what spoon material you might use to eat caviar is quite an interesting one. Because actually, even if the material is chemically inert, like something like ivory, there are several differences in the way that heat is taken from your tongue and your mouth. The texture is very important, so wooden spoons tend to give a particular sensation in the mouth which can be both pleasant or unpleasant depending on who you are.
- Previous Busting Blood Clots with Nanotechnology
- Next Why do wounds itch?








Comments
Add a comment