1
Physics, Astronomy & Cosmology / Re: Can you measure the one way speed of light without synchronised clocks?
« on: 19/04/2021 06:36:11 »
It should be fairly easy to calculate the one-way speed of light. The problem is doing so with any reasonable amount of accuracy.
Here's how I would do it.

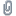 SpeedOfLight.gif (9.32 kB . 669x311 - viewed 45056 times)
SpeedOfLight.gif (9.32 kB . 669x311 - viewed 45056 times)
Light (strong laser) passes through two shaft connected spinning discs, hits a cylindrical (conical) mirror, and is projected onto a wall to record. Mostly interested in the trailing edge of the light spot.
Light speed is: 299,792,458 m/s.
So, say the two discs are spaced 10 meters apart, then it will have traversed the gap in about 1/(29,979,245) s
Say the discs are 2 meters in diameter, and spinning at 60,000 RPM (1,000 RPS). With a circumference of πD, or 6.28 m.
So, your discs are spinning at 6,280 m/s.
Multiply the two, and one gets about 1/4774 m, or .0002094 m (2x10-4)
Multiply by 1000, and one is 0.2094 mm
That is well within the range one can discern.
The problem is the accuracy of the reading. If one uses UV light, one might be able to get down to 100nm accuracy, or about 1x10-7 m.
So that gives one about 3 digits of accuracy. One may be able to add a 4th digit, or even 5th digit by going with a faster shaft speed, longer shaft, larger discs, etc. Perhaps using X-Rays if they could be reflected on the cylindrical mirror (or mirror pair).
So, the question is would say 3 or 4 digits of accuracy matter?
Now, let's consider some kind of unknown aether or fabric of space(time).
What is the fastest object known to man? well, Earth is a good candidate.
The equator is rotating at about 460m/s. And, even doubling it for the difference of forward rotation vs reverse rotation with respect to the fabric of space during the 24 hour day, and it still isn't fast enough.
Earth's orbital velocity around the sun is about 29,780,000 m/s, or about 1/10,000 the speed of light. And, still not fast enough to pick up. Earth's orbital speed around the Milky Way is about 220,000 m/s, and getting close to 1/1000 the speed of light. And, the Milky Way is moving at about 600,000 m/s.
Now, if our aether or fabric of space is not distorted by gravity, electrical fields, matter, etc, then one can choose a place to orient one's device East/West with respect to the galactic rotation or motion, or North/South with respect to the motion. This should give comparative velocities, but one is just barely on the cusp of being able to pick it up.
(oops, I got a conversion factor to mm off... but it means it is easier to snag the first digit of the speed of light with the theoretical machine, but still a difficult task to get multiple digits of accuracy).
Ok, thinking about this more, there are issues with the leading edge of the light from the first slot illuminating the trailing edge from the second slot making timing difficult.
One would likely fix that by either adding an adjustible flat mirror to the inbound light, or slightly changing the direction of the source. Adjust to both maximize the intensity of the output beam as well as maximizing the beam width coming off of the cylindrical mirror.
A concave mirror rather than a convex mirror would also work, but would flip the image. Parabolic?
Here's how I would do it.
Light (strong laser) passes through two shaft connected spinning discs, hits a cylindrical (conical) mirror, and is projected onto a wall to record. Mostly interested in the trailing edge of the light spot.
Light speed is: 299,792,458 m/s.
So, say the two discs are spaced 10 meters apart, then it will have traversed the gap in about 1/(29,979,245) s
Say the discs are 2 meters in diameter, and spinning at 60,000 RPM (1,000 RPS). With a circumference of πD, or 6.28 m.
So, your discs are spinning at 6,280 m/s.
Multiply the two, and one gets about 1/4774 m, or .0002094 m (2x10-4)
Multiply by 1000, and one is 0.2094 mm
That is well within the range one can discern.
The problem is the accuracy of the reading. If one uses UV light, one might be able to get down to 100nm accuracy, or about 1x10-7 m.
So that gives one about 3 digits of accuracy. One may be able to add a 4th digit, or even 5th digit by going with a faster shaft speed, longer shaft, larger discs, etc. Perhaps using X-Rays if they could be reflected on the cylindrical mirror (or mirror pair).
So, the question is would say 3 or 4 digits of accuracy matter?
Now, let's consider some kind of unknown aether or fabric of space(time).
What is the fastest object known to man? well, Earth is a good candidate.
The equator is rotating at about 460m/s. And, even doubling it for the difference of forward rotation vs reverse rotation with respect to the fabric of space during the 24 hour day, and it still isn't fast enough.
Earth's orbital velocity around the sun is about 29,780,000 m/s, or about 1/10,000 the speed of light. And, still not fast enough to pick up. Earth's orbital speed around the Milky Way is about 220,000 m/s, and getting close to 1/1000 the speed of light. And, the Milky Way is moving at about 600,000 m/s.
Now, if our aether or fabric of space is not distorted by gravity, electrical fields, matter, etc, then one can choose a place to orient one's device East/West with respect to the galactic rotation or motion, or North/South with respect to the motion. This should give comparative velocities, but one is just barely on the cusp of being able to pick it up.
(oops, I got a conversion factor to mm off... but it means it is easier to snag the first digit of the speed of light with the theoretical machine, but still a difficult task to get multiple digits of accuracy).
Ok, thinking about this more, there are issues with the leading edge of the light from the first slot illuminating the trailing edge from the second slot making timing difficult.
One would likely fix that by either adding an adjustible flat mirror to the inbound light, or slightly changing the direction of the source. Adjust to both maximize the intensity of the output beam as well as maximizing the beam width coming off of the cylindrical mirror.
A concave mirror rather than a convex mirror would also work, but would flip the image. Parabolic?
The following users thanked this post: jeffreyH