Catching Energy From the Sun

Electricity is pretty old - one of the oldest things ever really. The Universe is thought to be about 13.7 billion years old and electricity - the flow of charge - has been around for nearly all of it. But it is only in the last two centuries that humans have learnt how to make charges flow around circuits and do things for us; that is, make electricity. And Fifty years from now, our kids are going to look incredulously at us and ask – "you burnt things to get electricity?" We’ll answer – yes, but only until we realised how cheap and efficient renewable energy could be...

First, in considering electricity, we need to talk a bit about charge. We know three fundamental things about charge:

1. There are two types.

2. Different charges attract each other.

3. Like charges repel each other.

No one really knows why charges behave the way they do; it seems to just be a fact of our Universe.

Today, we know of eight ways to make charge flow. Some of the ways are familiar to everyday life, while others are less common and are less intuitive to understand. But they all have one thing in common - they are a way of moving charge from one place to another - generating electricity.

1. Static Electricity (charges moving when materials rub past each other)

This is the type of electricity that is responsible for lightning and why balloons stick to hair.

2. Chemical Electricity (charges moving when chemical reactions take place)

This type of electricity powers all of our batteries - from the small alkaline batteries in torches to the big lead-acid ones in cars. Nature has invented interesting ways to use electrochemistry:the electric eel is thought to have evolved about 500 million years ago, and through chemical reactions in special cells in the side of its body the eel can build up enough voltage to send a massive shock through its prey, stunning it for long enough so that it can kill it.

3. Piezoelectricity (charges moving when certain crystals are squeezed)

This type of electricity is generated when you squeeze the trigger on a gas lighter. As the piezoelectric crystal is compressed, charges move to either end. If you keep squeezing, the voltage can be big enough to ionize air and make mini-lightning - for example, the spark you see when you light a gas stove.

4. Pyroelectricity (charges moving when certain crystals are heated)

Although less commonly known, pyroelectricity happens when crystals similar to piezoelectric crystals are heated up, forcing different charges to opposite ends of the crystals. Their use isn't widespread, but they have applications as heat sensors and potentially in nuclear fusion generators.

5. The thermoelectric effect (charges moving by heating two different metals connected to each other).

This type of electricity relies on the intrinsic properties of metals and their densities. A thermoelectric generator is what is powering the Cassini-Huygens spacecraft - still orbiting Saturn. The heat in the Cassini-Huygens generator is provided by the radioactive decay of plutonium.

6. Nuclearvoltaics (charges flying off an atom as it radioactively decays)

Really big atoms (such as uranium or plutonium or caesium - pictured) are unstable. What this means is that after some time, they break up into smaller parts and some of these parts have charge. No-one has yet figured out a way to make any use of nuclear-voltaics to produce electricity due to the dangers of working with radioactive atoms.

7. Electromagnetism (charges moving due to moving magnets)

About 95% of the world's electricity is made by electromagnetism.

One of the fundamental things about our Universe is that when a magnet moves, electric fields flow.

Since the 19th century, we have been using coal, diesel, gas, water and the heat from nuclear decay, the tides, and the blowing winds to turn magnets inside wires to generate electricity.

It's a fantastic way of generating electricity, and will almost certainly be with us for a long time.

8. Photoelectricity (charges moving by the absorption of light).

The photovoltaic effect was discovered in 1839 by a French scientist named Alexander-Edmond Becquerel.

Becquerel used a platinum sheet covered in silver chloride and found that it generated electricity when light was shone on it.

Back then, the efficiency was less than 1% - but we've come a long way since then.

The reason why light can make electricity is a result of three things:

1. Light has energy;

2. Matter has charge;

3. When certain materials absorb light, these charges become excited and can move around.

Solar cells are devices designed to use these properties to make electricity.

Solar Cells

A solar cell is a little bit like a pool table, where the white ball represents a photon of light and the other balls are charge carriers.

When light (the white ball) is shone onto the solar cell (the pool table), it makes the charge carriers (coloured balls) move. And if the light has enough energy, it will excite the balls so much that they will travel to the edge of the solar cell (we need a special pool table here - one with pockets all along the outside) where they can be collected to make electricity. That's really it.

Of the easiest solar cells to understand are those made up of two types of material. One material has lots of free negative charge carriers (electrons). This is called n-type material.

The second is a material with lots of free positive charge carriers (called holes - the absence of electrons), which is called p-type material. When these two types are next to each other, an electric field is built up in the junction between them.

The important thing is that when light is shone on this structure, both positive and negative charges are formed. Because of the electric field between the p-type and n-type material, these charges are pushed to opposite edges of the cell.

So if you connect the two ends of the solar cell to external wires and complete the circuit then electricity can flow...

It's a remarkable device, and a truly amazing invention - for the interested reader who would like to learn more, the PVCDROM website is a great resource: http://www.pveducation.org/pvcdrom. For the reader who would like to learn more about the underlying physics of solar cell materials, the texts by Kittel "Introduction to Solid State Physics" and Sze "Semiconductor Devices" are excellent introductions.

Solar Cell Efficiency

Probably the most important measure of solar cells is efficiency.

In this context, what is usually meant by efficiency is the amount of electricity put out by the cell, compared to the amount of sunlight shining on it.

To be more precise, efficiency is defined as the ratio of electrical energy that comes out of the cell per second (the power) to the amount of light energy that hits the cell per second (incident energy).

η= (V x I)/(Incident Energy)

The symbol 'η' represents efficiency, V is voltage and I is current. The product of voltage and current (V x I) is the output power. For the structure discussed above - a single p-n junction, the maximum efficiency that anyone could ever get by placing it in direct sunlight is 31%.

So on a bright, sunny day, the theoretical limit to the amount of power you could get from a square metre of single p-n junction solar cells would be about 300 Watts - enough to power a microwave. The efficiency limitation is due to the colour of the sun and its distance from Earth.

Below is a diagram showing how much sunlight energy reaches the Earth. It shows the intensity (W) that falls on each square metre of earth (m^-2), per wavelength of light (nanometre^-1).

Now the thing is, somewhere on this diagram a vertical line has to be drawn. This line represents the band-gap of our solar cell material - the width of the pool table. The band-gap is the amount of energy a charge needs to absorb before it can become properly excited. It is called "the solar spectrum".

For light of energy higher than the band-gap (light to the left of our line), our charges will get excited and our solar cell will put out current. This is a good thing - we need current from our cell so that there are enough charges to power our light bulbs and toasters and hair dryers.

Light of energy less than the band-gap (to the right of the line) either doesn't get absorbed by the cell - passing right through, or get's absorbed in a not-useful way - generating heat. So to increase the amount of current from the cell, we need to move our band-gap line to the right - so that there is more light to the left of our line to absorb.

But, the power output of the cell is given by: Power (W) = Voltage (V) x Current (I)

This is important because it means that even if the current was very, very high, if we have a cell with low output voltage, then the output power will be low too. Now the voltage of the cell is directly related to the band-gap of the cell, increasing as the band-gap goes higher in energy - to the left in the above diagram.

So we have a trade-off:

And because efficiency η is given by: η=(Voltage x Current)/(Incident Energy), we have a maximum 'best-position' place on the spectrum for our line.

For sunlight on Earth, the 'best-position' line is at about 1200nm, corresponding to a maximum efficiency of about 31%.

Third Generation Photovoltaics

Now, we'd like to do better than 31%, and there are a couple of ways of doing it.

The first and most easy way is by concentrating light onto our solar cell. So if we can get a big magnifying glass, or a big mirror and focus it on our cell, it looks to the solar cell as if the Sun has got brighter - or a bit closer. This is because we're collecting light from a large area, and concentrating it on a smaller area. In this way, we can get a maximum efficiency of about 40%.

But we can go even better than this, and there are many, many ideas out there, ranging from up-converters and down-converters, to multi-exciton generation and quantum dots, to thermophotovoltaics, to selective contacts and hot-carrier cells.

In the last bit of this article, we'll discuss only two of these ideas: Multi-junction cells - the cells that currently hold the world record of efficiency, and Plasmonics - the beginnings of the next generation of nanostructured photovoltaics.

Multi Junction cells

Multi-junction cells broke the 40% efficiency barrier in 2009 and it's likely that 50% efficiency will be reached before 2020. Multi-junction cells are used on the Mars Rovers and the majority of the satellites orbiting the Earth right now to generate power.

How they get beyond 31% is by having more than one band-gap line on the solar spectrum. They do this by having a stack of cells, each with a band-gap slightly lower than the cell above it. In this way, the highest energy light (the purple) gets absorbed by the first cell - which is transparent to all light of lower energy (the blues, greens, yellows and reds). Then the second cell absorbs the next highest energy light after the purple (the blue) whilst being transparent to light of lower energy than this (the greens, yellows and reds), and so on.

The theoretical maximum efficiency for this type of cell is about 86%. This is the Carnot limit for sunlight energy conversion on Earth. There's no way of ever going beyond this limit on Earth - it's a fundamental limit. But we can keep getting closer.

Nanostructured Photovoltaics

This is going to be the next revolution of solar cell design. There's still no way of going beyond the fundamental efficiency limits, but there are going to be some new and exciting ways of getting closer to them.

One idea is plasmonics. A "plasmon" is the name given for a particular way that charge and light can resonate together. When the right wavelengths of light shine onto certain metals, the electrons inside the metal move back and forwards like a slinky spring. This moving backwards and forwards in turn sets up a moving electric field - and this coupling is called a plasmon. By structuring metals on the nanoscale these resonances can be tuned. Two of the ideas being applied to solar cells are those of nano-particle plasmonics and nanovoid plasmonics.

The idea is to use the electric field hotspots to increase absorption in exactly the region that you want to in a solar cell. In this way, light and charge can be guided to the optimal places in solar cells, increasing current, voltage and efficiency all in one structure.

Research into plasmonic photovoltaics is happening all over the world, including in the NanoPhotonics Centre in the Department of Physics at the University of Cambridge, where I am making solar cells on plasmonic nanovoids and seeing them shine.

How Semiconductors work

Silicon Electron Hole Pairs

Credit: 

Niraj Lal

Now, for the reader who would like to know more about the underlying physics of how the p-n junction works, we need a brief introduction to semiconductor physics.

The most common solar cell material is silicon, and it serves as a good example to use in discussing semiconductors. Silicon has four valence electrons which it likes to share with other silicons when it's in a crystal.

The little electron and hole in the diagram shows an electron becoming excited, leaving behind a 'hole' in the gap where the crystal would like it to be. In this case the required energy for exciting the electron has been given by the heat of the crystal - something that happens even at room temperature.

The interesting thing is that if a neighbouring electron popped into that hole - it would leave behind a hole at the place it just came from - physicists think of this as the hole itself moving.

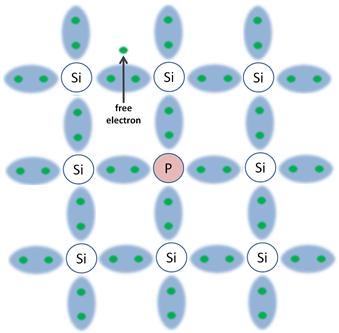
The previous diagram shows pure 'intrinsic' silicon. When you introduce another atom into the structure, such as phosphorus with an extra electron in the valence band, the amount of free electrons changes.

In the second diagram, the extra electron that was attached to the phosphorous atom has broken free (again due to the heat energy supplied at room temperature), and is now able to wander around in the crystal lattice. The material above is now called n-type silicon.

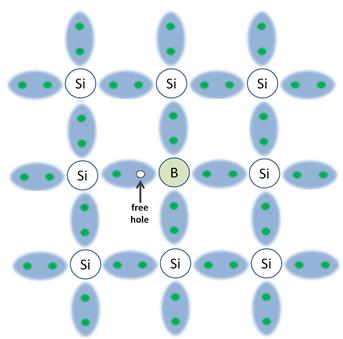
If, instead of phosphorous, we introduce boron into the structure, the amount of free holes increase. This is because boron has one less electron in its valence band.

In the third diagram, there is now a free hole that is able to wander about. The above material is then called p-type silicon.

The p-n structure is formed when these two types of material, p-type and n-type, come into contact with each other.

This region without any charge is called "the depletion region", and is what gives rise to the electric field in the middle of a solar cell.

That's the basic physics and it helps us to understand what's going on, but for real devices the actual method of making the p-n junction isn't quite done by sandwiching the two types together. The typical method is to add some boron atoms in the mix while the intrinsic silicon is crystallising - thus making p-type silicon. Later some phosphorous is driven into the wafer using gas deposition at high temperatures to make the top surface n-type, thus creating the junction.

The p-type and n-type come into contact	The electrons and holes recombine with each other	Once recombined, there are no longer any free charges

As an aside, this is the same field that exists inside a diode - allowing charge to flow easily in one direction (forward bias) and hardly at all in the other direction (reverse bias).

It is a truly remarkable device - and again the interested reader is referred to the texts of Kittel and Sze for a more thorough introduction.

Materials

The reader who has gotten this far might be interested in the different materials that solar cells can be made of. Lots of different materials are used, including inorganic semiconductors, organic semiconductors, and electrochemical solutions.

Within each of these sub-types there is still further variety in the type of materials being researched - within the inorganic semiconductors the range extends from silicon to germanium to compound semiconductors such as gallium-arsenide and cadmium-telluride, to name just a few. There also is expanding research in the field of quantum-dot and quantum well solar cells - cells made up of small particles of material embedded within a semiconductor which change their electric properties as their dimensions are varied.

Organic semiconductors work in a slightly differently way to inorganic semiconductors. Instead of having free charge carriers within a crystal lattice - charge carriers are associated more with individual molecules and polymers. This gives rise to different electrical properties, but the underlying physics of light-absorption remains the same. It is a relatively new field, and much research is being done on the particular organic materials that might work best.

Dye-sensitised solar cells are different again - in these cells a special dye absorbs light and rapidly transfers an excited charge into a solar cell substrate, the dye is then replenished via a conducting electrolyte solution. This too is a relatively recent invention.

Each of these device types are incredible inventions with their own particular advantages and disadvantages. Each material and device type has many researchers working on it - the interested reader is referred to the book by Martin Green "Third Generation Photovoltaics" (2003) for an introduction to the next generation of solar cell design.

As to which one is the best? We'll find out. But it's a promising field, with a bright future.