Every day we produce and use many different materials, but there is one which we rely on far more than any other: steel. It is truly the workhorse of all materials, with a long history and many uses, but that doesn't stop researchers using advanced experiments and theory to develop it further.
 |
| Figure 1. Continuous casting of steel bars. |
But what is steel? Basic steel is mostly iron with a little carbon mixed in, but more often than not steels also contain one or more other elements, with dozens to choose from.
In making the steel, the iron, carbon and other elements form an 'alloy', in which the elements are mixed together at the atomic scale, like salt dissolved in water. The precise composition (or recipe) of the steel and how it is produced determine its properties and, therefore, what it is useful for.
These properties can include how strong the steel is, how hard it is, how brittle it is and its ability to withstand the environment (i.e. not rust). It is the great versatility of steels, and their low cost, which means that they are by far the most commonly used metals in the world today.
We currently produce over 1.5 billion tonnes of steel per year worldwide, which is over ten times more than all the other metals combined. This figure has doubled since the late 1990s, and continues to rise. This is enough to fill over 75,000 Olympic-sized swimming pools each year, and equates to around 210 kg of steel for very person on the planet (the weight of three human adults).
Steel-making is big business, with over £200 billion worth of steel sold in 2011. Production is spread all over the globe, from here in the UK to Australia and China. Traditionally, most steel has been produced in countries undergoing industrial development. In recent history, there have been major steel-making centres in the UK (Sheffield), the USA (Pittsburgh) and Japan (Kobe), but this has since shifted to emerging and developing countries, like China, India and Brazil. Today, China makes over 45% of the world's steel.
Since steel is mainly iron, the production process starts with the mining of iron ore. This iron ore is 'smelted' by heating it along with coke (charcoal) and limestone in a blast furnace, in order to separate the iron metal from other elements. This results in a form of iron called 'pig iron', which contains too much carbon to be useful. This molten pig iron is then passed to the Basic Oxygen process, where impurities such as sulphur are removed and pure oxygen is blown through the molten iron to remove most of the carbon as carbon dioxide. Before this process, the pig iron has 4% carbon by weight, and afterwards this is reduced to between 0.1 and 1%.
Depending on the product being made, more elements can be added to the molten steel in measured amounts to help achieve the required properties. The steel is then either cast into continuous lengths to make bars for further processing or cast into large blocks called ingots. Continuously cast bars account for 96% of all steel produced. After casting they are cut up, heated and mechanically formed into the required shape. Examples include flat plates, pipes, I-shaped beams and rails.
Steel products are used extensively in our modern world, and we are never far from something which contains steel. Transportation, metal appliances and industrial components account for around 40% of total steel usage. Flat plates are typically used for vehicle and household appliance parts, whilst heavy industrial components may be formed from ingots. Unsurprisingly, construction and infrastructure uses the remaining 60%. Applications in this area include railway tracks, electricity pylons, oil and gas pipelines and structural supports.
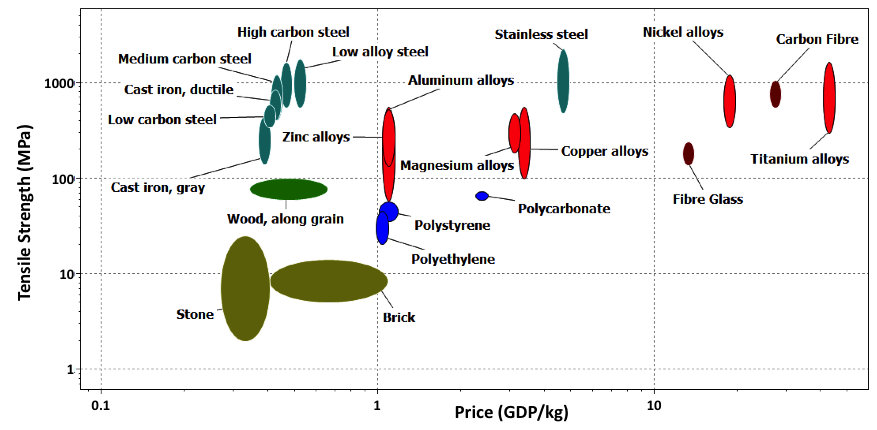 |
| Figure 2. Materials selection map showing tensile strength (i.e. strength when pulled) vs price for some well-known materials. Produced using the Cambridge Engineering Selection (CES) software package, Granta Design Ltd. |
For construction, the most common steels used are 'low carbon' steels. They comprise a small amount of carbon along with iron, and not much else. The main reason for their extensive use is simple - cost. No other material is so strong, tough and easily produced for such a low price. They also happen to bind well to concrete, making them ideal for use as reinforcing bars in reinforced construction concrete (probably the biggest single use of steel). However, not all steels are so cheap and simple. Typical low carbon steels may only cost around 40p/kg, but some stainless steels can cost over £5/kg and comprise numerous other elements aside from just iron and carbon.
 |
| Figure 3. Stamp on the back of a stainless steel fork, telling us it is made from a steel with 18% chromium by weight, and 0% nickel. |
The key ingredient in all stainless steels is chromium. The chromium forms a thin surface layer of chromium oxide, which protects the iron underneath and prevents rusting.
Stainless steels are used in the oil and chemical industries for containers which can store highly-corrosive acids and other substances. They are also used to make surgical instruments and cutlery. In fact, if you look on the back of pieces of cutlery, you may find some numbers stamped there, like 18/10 or 18/0. The number before the slash tells you the percentage of chromium in the steel, and the number after the slash tells you how much nickel has been added. In some applications, nickel is added to make the stainless steel tougher by changing the way the atoms arrange themselves.
'Superbainite' is a good example of a recent development in steel design. This steel has a very fine internal structure, which provides exceptional hardness and strength. What's more, it does not contain any expensive elements and does not require a complicated production route. It is already in use in modern-day military armour, and is a candidate for use in future jet engines.
It seems like steel is already used for so many things, and has been around for so long that there can't be much left to discover. However, there are many ways in which steels can be developed to help shape our future use of materials. There are two main goals for steel research at present: first, to enhance the properties of the material to allow it to be used for new applications, or to do a given job better; and second, to improve properties such that less material needs to be used in a given application, helping to reduce material consumption and costs. In order to achieve these goals, we not only focus on changing the compositions of steels, but also the way in which they are made, for instance how they are heated during production.
Steel has many varied uses and is able to do its job at a reasonable cost. New developments in steel design are driving costs and materials usage down, allowing us to face the environmental and economic challenges of tomorrow.
- Previous Beyond Mere Metals
- Next Why all decisions aren't made equally










Comments
Add a comment