Ingredients
 | Some Tea |  | A thermometer which measures from 30-100°C |
 | Some milk |  | A measure of some sort, that will measure the milk |
 | 2 identical mugs |
Instructions
We are trying to compare what happens to the temperature of milky tea when you add the milk at the beginning or at the end of a wait.
So make 2 identical cups of tea and pour a measured amount of milk into the first at the beginning of the experiment.
Wait 15 minutes then add the milk to the second cup of tea and measure the temperature of both cups.
Result
You should find that once you add the milk to the second cup, the cup which you added the milk to first is the warmest.
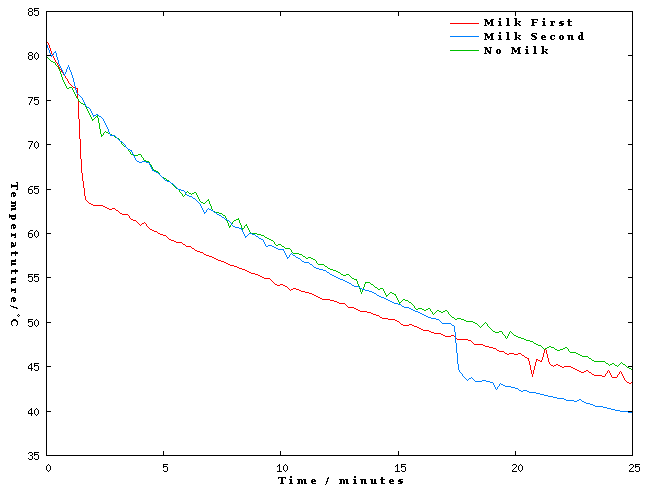
Below you can see a graph of the temperature of the tea against time made with a mutilated electronic thermometer plugged into a computer. You can see that the tea which has milk added first cools down more slowly than the tea with no milk in it. So when you add the milk to the second cup of tea it ends up colder.
Explanation
Adding the milk lowers the temperature of the tea but it doesn't do this by removing energy, it does it by spreading the energy around.
The hotter the tea the bigger the difference in temperature is between it and the room. This big temperature difference means that heat energy is lost more quickly so the tea without milk in cools more quickly than the the one you added milk to at the start. So during the experiment the cup with no milk will loose more heat, but should still always be warmer than the cup with milk. That is until you add milk to it when it will become significantly colder.
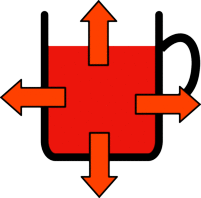 | 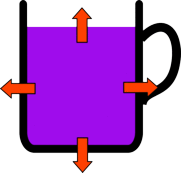 |
| Hot tea is much warmer than the surroundings so it looses heat quickly. | Warm tea is only slightly warmer than its surroundings so it only looses heat slowly. |
Because in the end both cups of tea are identical, at the end the one with the most energy will be the hottest. This means that the tea which had the milk added first has lost less energy so will end up warmer.
- Previous Strange Textures
- Next Jumping Flames










Comments
The temperature difference is
The temperature difference is one factor, but the specific heat capacity of milk is lower, meaning the mixture is a better insulator. I guess this must be negligible though.
Thought about this for a long
Thought about this for a long time and didn't expect the difference to be so big.
One thing I wondered about was if the increased volume helps with cooling, but it's probably the opposite: A half empty cup has a larger surface area than a full cup.
Thanks for the experiment! And I'm amazed I could find it with a google search...
you needed a fourth cup with
you needed a fourth cup with tea and milk that was heated to the same temperature as the tea that didn't ever have milk in it, so we could see four lines on the chart
You didn't take the warming
You didn't take the warming of the milk into account. If you take it out of the fridge just before adding it in both cases, then the answer is indeed trivial.
what?
what?
Milka, you are right. Adding
Milka, you are right. Adding cold milk to hot tea will result in a hotter mix over time than adding cold milk to cool tea. The two teacups are not on equal thermodynamic footing. One takes a dose of cold when it is hot. The other takes the same dose Of cold when it is cooler. The relative "hit" is larger in the second instance, obviously. Unless the milk is left out of the fridge to warm up before being put into the second cup, the answer is indeed trivial.
The key difference between the two scenarios is not the time lapse between adding the milk. The key difference is that in one case the system is left to cool unobstructed, and in the other, part of the system is kept refrigerated (with an energy expense) and then added. If the energy expended to refrigerate the milk poured into the second cup were added back into that same cup, there would be no temperature difference between the two teas at the end.
In other words, putting the milk in first does not require you to keep the milk cold. Putting the milk in later, does. Putting the milk in later requires energy expended to keep that milk the same temperature as the milk put into the first cup. So when the milk is added later, thermodynamic account needs to be taken of that energy expense. But that expense is in the refrigerator, so the second cup is measured at a lower temperature because the refrigeration expense is not taken into account.
If each cup were isolated in a thermodynamic system, then the sum of the temperatures of the tea, the cup, and the refrigerator, would be equal. The discrepancy we find in the real world of tea temperatures only arises because we forget the thermodynamic system includes the milk refrigerator. One cup of tea might be warmer if you pour the milk in first, but the other, cooler cup, comes with more warm air expelled from your fridge. Just enough to make up the difference.
Thanks. My wife and I were
Thanks. My wife and I were debating this and Google and you helped out!
Great scientific method and
Great scientific method and explanation!
Was wandering about this today and you did the test perfectly.
Undeniable results! Good science!
My husband and I were
My husband and I were debating this too! You seem like a smart intellectual, want to hang out some time? I can see us becoming good buddies.
Add a comment